地震液化中地下結構上浮離心機試驗的精細化模擬方法與流程
本發明屬于巖土工程研究領域,尤其涉及一種地震液化中地下結構上浮離心機試驗的精細化模擬方法。
背景技術:
飽和松散砂土地基在地震荷載作用下會發生液化,宏觀上表現為土體中孔隙水壓力上升,同時土體固相的有效接觸應力為零,這時土體性質類似于流體并喪失抗剪強度。地震液化造成以下危害:例如房屋傾斜、地基沉降、地鐵隧道上浮、道路路基滑移等。
液化大變形中地下結構遭受嚴重破壞的典型案例是在1995年神戶地震中大開地鐵車站嚴重受損,之后地下結構的抗震分析和抗減震研究開始受到高度重視。神戶震害的調查表明,強震液化引起飽和土體的大變形是引發地下結構變形和失穩破壞的重要原因。所以,與一般結構物的抗震分析不同,地下結構的動力分析并非單純的結構動力響應問題,而是一個需要綜合考慮水-土-結構耦合體系的動力問題。現在通過離心機施加數十倍的重力加速度,可以在離心機試驗中模擬實際液化場地中地下結構上浮過程。同時對于這樣的離心機試驗,人們希望可以數值模擬液化時離散顆粒土體-地下結構之間的非連續動力接觸問題,同時希望有效控制離散顆粒模擬規模以節省模擬時間,因此出現了流體與地下結構-近場離散顆粒-遠場連續固相土體耦合的精細化模擬方法(見文獻“金煒楓,周健.引入流體方程的離散顆粒-連續土體耦合方法研究[j].巖石力學與工程學報,2015,34(6):1135~1147”),但是在這種方法中遠場連續土體和流體使用有限元網格,在地震液化大變形發展過程中存在網格畸變,從而造成模擬中斷的問題。
技術實現要素:
本發明為了克服現有方法的不足,即現有的基于地下結構-近場離散顆粒-遠場連續固相土體與流體耦合的方法,在精細化模擬地下結構在可液化砂土中地震響應離心機試驗時,存在網格畸變造成模擬中斷的問題,因此本發明用無網格方法中rkpm方法(reproducingkernalparticlemethod)來離散遠場連續固相土體區域以及流體方程,從而使遠場連續固相土體模型和流體與近場離散顆粒一樣,可以適應地震液化大變形分析,本發明還構建了流體與離散顆粒-連續固相土體以及地下結構的耦合框架,基于上述工作避免了地震液化大變形模擬過程中因網格畸變造成模擬中斷的問題。
本發明涉及一些簡寫和符號,以下為注解:
rkpm:指無網格法中的重構核粒子法(reproducingkernalparticlemethod,rkpm),簡稱rkpm方法,相比傳統的需建網格的有限元和有限差分方法,利用rkpm方法建立的連續土體模型和流體模型可以適應地震大變形分析,不會出現網格畸變造成模擬中斷的問題。
ale:指任意拉格朗日-歐拉項(arbitrarylagrangian-eulerian,ale),簡稱ale項,當流體方程用rkpm方法離散后ale項中的參考坐標系速度表現為rkpm點的移動速度,這時通過指定ale項中的參考坐標系速度可以指定流體rkpm點的移動速度與地下結構邊界相同、或與離散顆粒相同、或與連續土體rkpm質點相同。
本發明為解決上述技術問題采用以下技術方案:
本發明提供一種地震液化中地下結構上浮離心機試驗的精細化模擬方法,具有以下特點:(1)固相土體用含過渡域的離散顆粒-rkpm連續土體耦合方法建模,在過渡域上離散顆粒和連續土體rkpm點重合且有相同位移,靠近結構的細觀分析區域用離散顆粒模擬,其它區域用連續模型模擬;(2)流體方程基于ale描述以實現流體rkpm質點的速度控制,當與顆粒耦合時可直接實現液化模擬,而與連續土體耦合時通過引入finn液化模型實現液化模擬;(3)離散-連續固體與流體的耦合框架為流體rkpm點分別與離散顆粒和連續土體rkpm質點重合,用地下結構邊界、離散顆粒和連續土體rkpm質點的移動速度來指定流體rkpm點的移動速度。具體步驟如下:
步驟1:建立地下結構有限元模型、建立地下結構附近的土體離散顆粒模型、建立遠離地下結構的rkpm固相連續土體模型;
步驟2:用rkpm方法離散流體方程;
步驟3:建立rkpm流體與地下結構-離散顆粒-連續土體模型的液化耦合框架;
步驟4:模擬地震液化中地下結構上浮的離心機試驗。
其中,
(1)所述步驟1中,地下結構有限元模型、土體離散顆粒模型、rkpm固相連續土體模型以及它們的耦合形式分述如下:
(1.1)地下結構有限元模型用有限元中的梁單元。
(1.2)土體離散顆粒模型中顆粒的運動方程包含平動方程和轉動方程。
(1.3)rkpm固相連續土體模型指用rkpm方法(reproducingkernalparticlemethod)建立連續土體模型,rkpm核函數采用用三次樣條函數。
(1.4)離散顆粒和連續土體之間的銜接方式如下:離散顆粒和連續土體之間有部分重疊的耦合過渡域,耦合過渡域上每個離散顆粒和連續土體rkpm質點一一對應耦合且位移、速度和加速度相等。
(1.5)地下結構有限元模型與離散顆粒模型耦合的具體方法為:通過保證耦合邊界上力和速度的連續性來實現有限元-離散顆粒耦合,將有限元模型中耦合邊界邊界節點速度傳遞至離散顆粒模型中,并將此速度作為離散顆粒的速度邊界。
(2)所述步驟2中:
(2.1)用來離散流體方程的rkpm方法采用的核函數為三次樣條函數。
(2.2)用rkpm方法進行離散的流體微分方程包含質量和動量守恒方程,流體微分方程中含參考坐標系ale項和流固耦合項,這里的ale項指任意拉格朗日-歐拉項(arbitrarylagrangian-eulerian,ale),簡稱ale項,當流體方程用rkpm方法離散后ale項中的參考坐標系速度表現為rkpm點的移動速度,這時通過指定ale項中的參考坐標系速度可以指定流體rkpm點的移動速度與地下結構邊界相同、或與離散顆粒相同、或與連續土體rkpm質點相同;用rkpm方法建立的流體模型可與細觀顆粒耦合液化,也可與連續固相土體模型耦合液化。
(3)所述步驟3中,rkpm流體與地下結構-離散顆粒-連續土體模型的液化耦合框架為:
(3.1)流體方程離散后的rkpm點和離散顆粒及連續土體rkpm點重合。
(3.2)且基于流體方程中的ale項,用地下結構邊界速度、固體rkpm質點速度和離散顆粒速度指定流體rkpm點移動速度。
(3.3)流體方程離散后的rkpm點與離散顆粒耦合時可直接實現液化模擬,而與連續土體rkpm點耦合時通過引入finn液化模型實現液化模擬。
(4)所述步驟4中,模擬地震液化中地下結構上浮的離心機試驗的具體方法為:通過在數值模型底部施加地震加速度,模擬水-土-地下結構耦合體系在液化過程中的動力響應,分析液化土體大變形的發展機制、離散砂土與結構的非連續動力接觸作用、以及結構的上浮位移曲線、加速度曲線和彎矩。
本發明采用以上技術方案與現有技術相比,具有以下技術效果:現有的基于地下結構-近場離散顆粒-遠場連續固相土體與流體耦合的方法,在精細化模擬地下結構在可液化砂土中地震響應離心機試驗時,存在網格畸變造成模擬中斷的問題,因此本發明用無網格方法中rkpm方法(reproducingkernalparticlemethod)來建立遠場連續固相土體模型以及全域流體模型,還構建了rkpm流體與離散顆粒-連續固相土體以及地下結構的耦合框架,從而使遠場連續固相土體模型和流體模型可以與近場離散顆粒一樣,可以適應地震液化大變形分析,避免已有方法中網格畸變造成模擬中斷的問題。
附圖說明
圖1可液化土中地下結構原型示意圖;
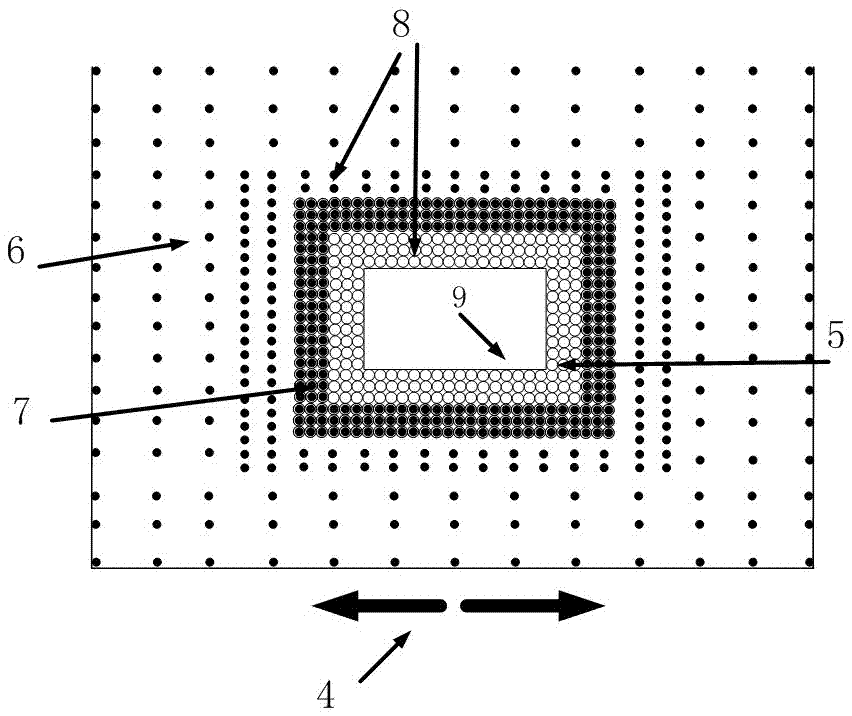
圖2為rkpm流體與離散顆粒-連續固相土體以及地下結構的耦合框架示意圖;
圖3為離散顆粒-rkpm連續固相土體耦合圖;
圖4為離散顆粒與地下結構梁單元邊界耦合圖;
圖中1.地下結構,2.可液化的飽和砂土,3.模型箱邊界,4.模型箱底部的地震動載荷,5.離散顆粒,6.連續固相土體rkpm點,7.離散顆粒-rkpm連續固相土體耦合過渡域,8.與離散顆粒及連續固相土體rkpm點重合的流體rkpm點,9.地下結構梁單元有限元模型,10.地下結構的一個梁單元,11.梁單元第一節點,12.梁單元第二節點。
具體實施方式
為了使本發明實現的技術手段、創新特征、達成目的與功效易于明白了解,下面結合具體圖示,進一步闡述本發明。
本發明涉及一些簡寫和符號,以下為注解:
rkpm:指無網格法中的重構核粒子法(reproducingkernalparticlemethod,rkpm),簡稱rkpm方法,相比傳統的需建網格的有限元和有限差分方法,利用rkpm方法建立的連續土體模型和流體模型可以適應地震大變形分析,不會出現網格畸變造成模擬中斷的問題。
ale:指任意拉格朗日-歐拉項(arbitrarylagrangian-eulerian,ale),簡稱ale項,當流體方程用rkpm方法離散后ale項中的參考坐標系速度表現為rkpm點的移動速度,這時通過指定ale項中的參考坐標系速度可以指定流體rkpm點的移動速度與地下結構邊界相同、或與離散顆粒相同、或與連續土體rkpm質點相同。
finn:指finn液化模型(可參考文獻“marting.r.,finnw.d.l.,seedh.b.,fundamentalsofliquefactionundercyclicloading[j].journalofthegeotechnicalengineeringdivision,1975,101(n5):423-438.”),在本發明中將finn液化模型引起的液化孔壓增量轉變為體力加入流體方程中,從而當流體rkpm點與連續固相土體rkpm點耦合時可以模擬地震液化現象。
a:地下結構有限元模型中梁單元截面積。
eiz:地下結構有限元模型中梁單元剛度。
l:地下結構有限元模型中梁單元桿長。
[ke]:地下結構有限元模型中梁單元剛度矩陣。
m:離散顆粒質量。
fx:作用在離散顆粒上x方向合力。
fy:作用在離散顆粒上y方向合力。
mxy:離散顆粒所受xy方向轉矩。
i:離散顆粒轉動慣量。
di:兩個rkpm質點距離。
d:兩個rkpm質點距離與影響半徑比值,即
φ(d):rkpm核函數,本發明中采用三次樣條函數。
c:流體聲速,是流體密度和體積模量的函數。
ρ:流體密度。
ux:流體x方向流速。
uy:流體y方向流速。
t:流體方程中的時間變量。
n:流體方程中局部微小區域多孔介質平均孔隙率。
τxy:流體剪應力。
p:流體孔壓。
bx:x方向流體體力。
by:y方向流體體力。
(fint)x:x方向流固耦合作用力。
(fint)y:y方向流固耦合作用力。
如圖1-4所示,本發明提供一種地震液化中地下結構上浮離心機試驗的精細化模擬方法,具有以下特點:(1)固相土體用含過渡域7的離散顆粒-rkpm連續土體耦合方法建模,在過渡域7上離散顆粒5和連續土體rkpm點6重合且有相同位移,靠近地下結構1的細觀分析區域用離散顆粒5模擬,其它區域用連續固相土體rkpm點6模擬;(2)流體方程基于ale描述以實現流體rkpm質點8的速度控制,當與離散顆粒5耦合時可直接實現液化模擬,而與連續固相土體rkpm點6耦合時通過引入finn液化模型實現液化模擬;(3)離散-連續固體與流體的耦合框架為流體rkpm點8分別與離散顆粒5和連續固相土體rkpm質點6重合,用地下結構1邊界、離散顆粒5和連續土體rkpm質點6的移動速度來指定流體rkpm點8的移動速度。具體步驟如下:
步驟1:建立地下結構有限元模型、建立地下結構附近的土體離散顆粒模型、建立遠離地下結構的rkpm固相連續土體模型,這三類模型及其耦合分述如下;
(1.1)地下結構有限元模型9用梁單元11,設a、eiz和l分別為梁的截面積、剛度和桿長,設[ke]為梁單元剛度矩陣,則梁單元剛度矩陣[ke]為:
(1.2)土體離散顆粒模型5中顆粒的運動方程包含平動方程和轉動方程:
平動方程:
轉動方程:
上式中m為離散顆粒質量,
(1.3)rkpm固相連續土體模型指用rkpm方法(reproducingkernalparticlemethod)建立連續土體模型,在空間上形成連續固相土體rkpm點6,設
(1.4)離散顆粒和連續土體之間的銜接方式如下:
離散顆粒和連續土體之間有部分重疊的耦合過渡7,耦合過渡域7上每個離散顆粒和連續土體rkpm質點一一對應耦合且位移、速度和加速度相等。
(1.5)地下結構有限元模型9與離散顆粒模型5耦合的具體方法為:
通過保證耦合邊界上力和速度的連續性來實現有限元-離散顆粒耦合,例如在圖4中將地下結構有限元模型9中的一個梁單元10上第一節點11和第二節點12的速度傳遞至離散顆粒模型5中,并將此速度作為離散顆粒模型5的速度邊界。
步驟2:用rkpm方法離散流體方程,
(2.1)用來離散流體微分方程的rkpm方法中采用的核函數為三次樣條函數,如式(4)所示。
(2.2)用rkpm方法進行離散的流體微分方程包含質量和動量守恒方程,流體方程中含參考坐標系ale項和流固耦合項,此全域流體方程可與細觀顆粒耦合液化,也可與連續固相土體模型耦合液化,流體微分方程如下;
流體質量守恒:
流體動量守恒(x方向):
流體動量守恒(y方向):
其中c為流體聲速,是流體密度和體積模量的函數,反映流體的微可壓縮性;ρ為流體密度;ux和uy分別為流體x和y方向流速;t為流體方程中的時間變量;n為局部微小區域多孔介質平均孔隙率;τxy為流體剪應力;p為流體孔壓;bx和by分別為x和y方向流體體力;(fint)x和(fint)y分別為x和y方向流固耦合作用力;單下劃線項為任意拉格朗日-歐拉項(arbitrarylagrangian-eulerian,ale),簡稱ale項,其中
當流體與連續土體耦合時,finn液化模型中的孔壓增量轉化為等效流體豎向體力,設
步驟3:建立rkpm流體與地下結構-離散顆粒-連續土體模型的耦合框架,具體形式如下:
(3.1)流體rkpm點8和離散顆粒5及連續固相土體rkpm點6重合。
(3.2)基于流體方程中ale項中參考坐標系移動速度
(3.3)流體方程離散后的rkpm點8與離散顆粒6耦合時可直接實現液化模擬,而與連續土體rkpm點6耦合時通過引入finn液化模型實現液化模擬。
步驟4:模擬地震液化中地下結構上浮的離心機試驗:具體方法為:通過在數值模型底部施加地震動載荷4,即施加地震加速度,模擬水-土-地下結構耦合體系在液化過程中的動力響應,分析液化土體大變形的發展機制、離散顆粒5與地下結構結構1的非連續動力接觸作用、以及地下結構1的上浮位移曲線、加速度曲線和彎矩。
- 還沒有人留言評論。精彩留言會獲得點贊!