非線性遲滯動力學模型參數識別的粒子群新算法的制作方法
本發明涉及非線性遲滯動力學模型參數識別的粒子群新算法,屬于非線性遲滯系統參數識別、群智能算法的領域。
背景技術:
遲滯特性作為一種非線性動力學特性,廣泛存在于橡膠、壓電陶瓷、磁流變等材料中。在對此類材料進行非線性動力學分析時,為了建立準確的動力學模型,需采用非線性遲滯動力學模型。非線性遲滯動力學模型能夠準確模擬結構的非線性遲滯特性,但具有較多的模型參數,需要利用優化算法進行識別。由于非線性遲滯動力學模型的參數較多,彼此之間存在耦合,這使得對模型參數準確、快速識別的難度大大增加。
針對非線性遲滯動力學模型的特點,國內外提出了許多參數識別方法,如最小二乘法、遺傳算法、帝國主義競爭算法、粒子群算法等。其中粒子群算法,由于具有收斂迅速、原理簡單、易于實現的特點,被廣泛運用于多目標優化、模式識別、信號處理、損傷識別等領域。但是標準粒子群算法作為一種隨機搜索算法,容易陷入局部極值,發生早熟收斂,無法獲得真正的最優解。為了克服標準粒子群算法的這些缺點,對標準粒子群算法的改進措施多集中于修改算法的慣性系數,引入新的機制,以及將標準粒子群算法同其他智能算法混合。
技術實現要素:
發明目的:針對上述現有技術,提出一種非線性遲滯動力學模型參數識別的粒子群新算法,改進標準粒子群算法的收斂性能,保證粒子群算法在前期迭代過程中的全局尋優能力以及后期迭代過程中的局部尋優能力。
技術方案:非線性遲滯動力學模型參數識別的粒子群新算法,包括如下步驟:
步驟1,讀入包含試驗狀態與遲滯回線在內的試驗數據;
步驟2,初始化粒子群,將D個代表待識別參數的N維粒子隨機布置在搜索域內;
步驟3,利用D個粒子的N維參數,調用非線性遲滯動力學模型的分析模塊,計算全體粒子的遲滯回線;
步驟4,計算各個粒子的遲滯回線計算值與試驗值之間的差距,利用適應度函數確定各個粒子的適應度值;
步驟5,通過將各個粒子的適應度值與各個粒子的歷史最優適應度值以及全局最優適應度值比較,更新各個粒子的歷史最優位置和粒子群的全局最優位置;
步驟6,利用步驟5中確定的各個粒子新的歷史最優位置和粒子群新的全局最優位置,更新各個粒子的位置;
步驟7,當算法達到最大迭代步數時,輸出識別結果,完成整個識別過程。
進一步的,步驟4所述遲滯回線計算值與試驗值之間的差距,利用公式計算;其中,M為遲滯回線試驗值的個數,ωi為遲滯回線第i個試驗值的權系數,為第i個試驗值的縱坐標,為第i個試驗值的橫坐標處遲滯回線計算值的縱坐標。
進一步的,步驟4所述適應度函數為其中a為平移因子,b為縮放因子。
進一步的,所述平移因子a和縮放因子b的確定方法為:首先,利用標準粒子群算法對模型參數進行一次識別,確定適應度隨迭代步的變化趨勢,假設第1迭代步和最大迭代步J時,利用識別的模型參數計算得到的遲滯回線計算值與試驗值之間的差距分別為e1和eJ,縮放因子b等于(x2-x1)/(e1-eJ),平移因子a等于x1-eJ(x2-x1)/(e1-eJ);其中[x1,x2]為區間,x1∈[0.15,0.35],x2∈[2.5,4]。
有益效果:(1)本發明通過定義適應度函數改進了標準粒子群算法的收斂性能,保證了算法在前期迭代過程中的全局尋優能力以及后期迭代過程中的局部尋優能力,避免算法陷入局部極值,發生早熟收斂,無法獲得真正的最優解。
(2)本發明能夠實現對非線性遲滯動力學模型參數準確、快速地識別,可以廣泛運用于各類非線性遲滯動力學模型的參數識別。
附圖說明
圖1是本發明的算法流程圖;
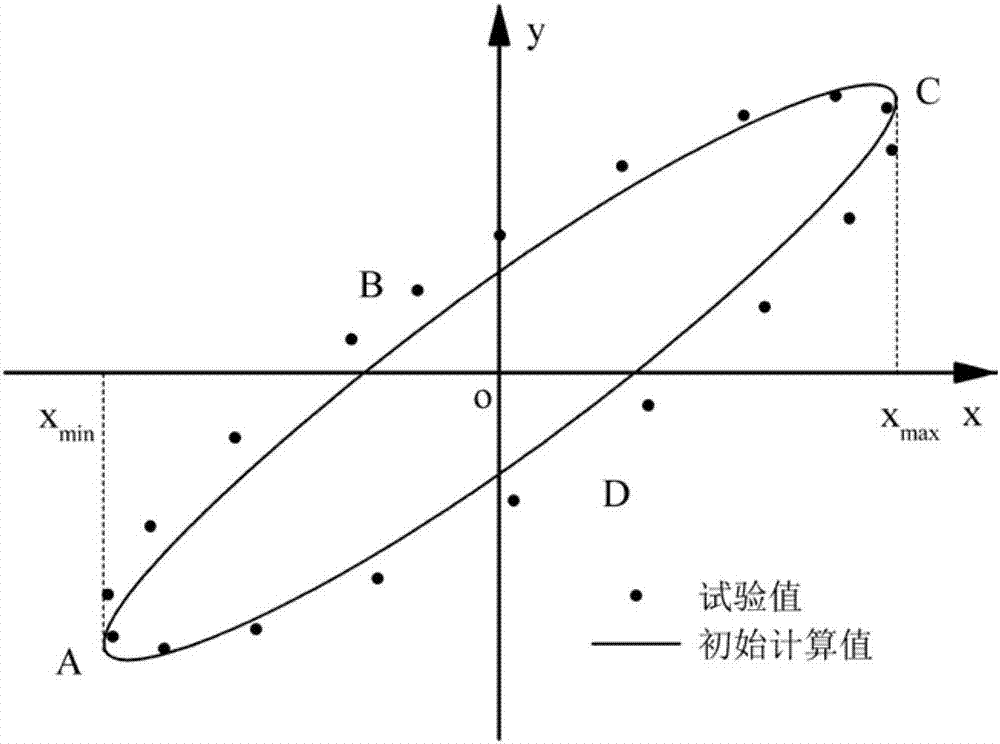
圖2是遲滯回線示意圖;
圖3是函數y=1/x的示意圖;
圖4是NACA0012翼型的迎角-法向力系數遲滯回線;
圖5是NACA0012翼型的適應度均值收斂曲線;
圖6是滯彈位移場模型的應變-應力遲滯回線;
圖7是滯彈位移場模型的適應度均值收斂曲線。
具體實施方式
下面結合附圖對本發明做更進一步的解釋。
如圖1所示,本發明非線性遲滯動力學模型參數識別的粒子群新算法,包括如下步驟:
步驟1,讀入包含試驗狀態與遲滯回線在內的試驗數據。遲滯回線的試驗值與利用粒子初始參數得到的遲滯回線計算值如圖2所示。遲滯回線試驗值的坐標為(i=1,2,…,M),M為遲滯回線試驗值的個數,為第i個試驗值的橫坐標,為第i個試驗值的縱坐標;遲滯回線計算值的坐標為(k=1,2,…,K),K為遲滯回線計算值的個數,為第k個遲滯回線計算值的橫坐標,為第k個遲滯回線計算值的縱坐標。讀入遲滯回線試驗值時,從橫坐標最小值處開始按順時針方向讀到橫坐標最大值處,再讀回橫坐標最小值處,即圖2中A-B-C-D-A的讀入順序。
步驟2,初始化粒子群,將D個代表待識別參數的N維粒子隨機布置在搜索域內。N維粒子對應需要識別的N個模型參數。第d個粒子的第n個模型參數的初始值記為(d=1,2,…,D;n=1,2,…,N)。
步驟3,利用D個粒子的N維參數,調用非線性遲滯動力學模型的分析模塊,計算各個粒子對應的遲滯回線。非線性遲滯動力學模型方程的一般形式為:
y=F(x,c1,c2,…,cN) (1)
其中,c1,c2,…,cN即為待識別的N個模型參數。對于第d個粒子,利用公式(1)以及(n=1,2,…,N)即可得到其對應遲滯回線的計算值的坐標(k=1,2,…,K)。遲滯回線計算值同樣按照A-B-C-D-A的順序排列。
步驟4,由于遲滯回線計算值與試驗值的橫坐標不同,計算各個粒子的遲滯回線計算值與試驗值之間的差距時,需首先利用與試驗值橫坐標臨近的計算值,線性插值確定橫坐標處對應的計算值(i=1,2,…,M)。再利用下式確定遲滯回線計算值與試驗值之間的差距:
其中,ωi為遲滯回線第i個試驗值的權系數,即為第i個試驗值的橫坐標處遲滯回線計算值的縱坐標。
遲滯回線計算值與試驗值之間的差距越小,說明識別的模型參數越好。適應度值作為評價各個粒子的N個模型參數優劣的依據,如果直接將遲滯回線計算值與試驗值之間的差距作為適應度值,那么前期迭代過程中各個粒子的適應度值差距較大,各個粒子會向其中最優的粒子方向收斂,發生早熟收斂;后期迭代過程中各個粒子的適應度差距較小,會使各個粒子陷入局部極值。這使得計算得到的最優位置可能并非真正的最優位置,識別出的參數也可能并非最優解。如果一個函數可以將前期迭代過程中各個粒子的適應度值差距縮小,將后期迭代過程中各個粒子的適應度值差距放大,那便可以克服標準粒子群算法的這些缺點。本發明采用下式定義適應度函數,
本發明定義的適應度函數值越大,說明遲滯回線的計算值與試驗值越接近,識別的模型參數越好。本發明定義的適應度函數基于函數y=1/x,如圖3所示。從圖3可以看出,當x小于1時,x的變化對y影響較大;當x大于1時,x的變化對y影響較小。如果x對應于遲滯回線計算值與試驗值之間的差距ed,利用平移因子a和縮放因子b可以將ed布置在合理區間[x1,x2],使得ed在前期迭代過程被縮小,在后期迭代過程被放大。
為了確定平移因子a和縮放因子b,首先,需利用標準粒子群算法對模型參數進行一次識別,確定適應度隨迭代步的變化趨勢。假設第1迭代步和最大迭代步J時,利用識別的模型參數計算得到的遲滯回線計算值與試驗值之間的差距分別為e1和eJ。為了將區間[eJ,e1]轉換到圖3中的區間[x1,x2],縮放因子b等于(x2-x1)/(e1-eJ),平移因子a等于x1-eJ(x2-x1)/(e1-eJ)。對于區間[x1,x2],x1不能過于靠近0,x2不能遠大于1,否則會使得改進粒子群算法在后期和前期迭代步需要消耗過多迭代步才能收斂。x1適宜的取值區間為[0.15,0.35],x2適宜的取值區間為[2.5,4]。實施實例中,[x1,x2]對應的區間為[0.2,3]。
步驟5,將各個粒子在之前的迭代過程中,適應度值最大時的N維參數,稱為粒子的歷史最優位置,第d個粒子在第j迭代步的歷史最優位置記為將全體粒子在之前的迭代過程中,適應度值最大時的N維參數稱為全局最優位置,第j迭代步的全局最優位置記為通過將各個粒子的適應度值與各個粒子的歷史最優適應度值以及全局最優適應度值比較,更新各個粒子的歷史最優位置和粒子群的全局最優位置。
步驟6,利用步驟5中確定的各個粒子新的歷史最優位置和粒子群新的全局最優位置,更新各個粒子的位置,即指粒子對應的N維參數。在第j迭代步,第d個粒子的第n個參數按下式迭代更新:
其中,為第j迭代步,第d個粒子的第n個參數的速度,a1和a2為[0,2]區間的加速度系數,r1和r2為[0,1]區間的隨機數,w為慣性系數,隨著迭代步數按下式線性遞減:
其中,wmax和wmin分別為慣性系數的最大值和最小值,J為最大迭代步數。
步驟7,當算法達到最大迭代步數J時,各個粒子均收斂于同一位置,此位置即為非線性遲滯動力學模型參數的識別結果,即
其中,為第n個模型參數在第J迭代步的識別結果。輸出識別結果,完成整個識別過程。
實施實例:
為了體現本發明的實際效果,采用本發明的參數識別方法,分別識別了兩種非線性遲滯動力學模型,即Leishman-Beddoes動態失速模型與粘彈阻尼器的滯彈位移場模型的參數。這兩種模型對于分析直升機旋翼氣彈動力學問題,提高旋翼氣彈穩定性都非常重要。需要說明的是此處的實施實例僅僅用于解釋本發明,并不用于限定本發明。
實例1.翼型迎角動態變化時,由于氣流分離與動態失速的作用,翼型剖面的迎角-法向力系數曲線呈現滯回現象。利用Leishman-Beddoes動態失速模型能夠準確計算翼型氣動力隨迎角的變化,但該模型具有較多的模型參數,需要利用試驗數據進行識別。
利用本發明提出的粒子群新算法,識別了翼型的Leishman-Beddoes動態失速模型的參數。粒子群算法中布置的粒子數為10,迭代步數為100,重復次數為50。
NACA0012翼型,弦長0.1米,來流馬赫數為0.38,迎角變化為α=10.3°+8.1°sin(0.075S)。50次重復識別后,利用識別的最優模型參數計算得到的翼型迎角-法向力系數遲滯回線如圖4所示,適應度的均值收斂曲線如圖5所示。
從圖4可以看出,本發明能夠準確識別Leishman-Beddoes動態失速模型的參數,計算得到翼型迎角-法向力系數遲滯回線同試驗值非常吻合。從圖5可以看出,對于Leishman-Beddoes動態失速模型的參數識別問題,相比于標準粒子群算法,本發明能夠更準確、快速地收斂于最優解,具有比標準粒子群算法更好的收斂性能。
實例2.由金屬和橡膠構成的粘彈阻尼器,能夠增加結構的剛度與阻尼,起到耗能減振的作用,被廣泛運用于航空航天,高層建筑,機械工程等各個領域。在交變載荷作用下,粘彈阻尼器的應變與應力之間會呈現非線性遲滯特性。
滯彈位移場模型能夠準確模擬粘彈阻尼器的應力-應變遲滯回線,其模型參數需要利用試驗數據進行識別。
利用本發明提出的粒子群新算法,識別了粘彈阻尼器滯彈位移場模型的參數。粒子群算法中布置的粒子數為10,迭代步數為100,重復次數為50。粘彈阻尼器所受交變載荷的頻率為4赫茲。
50次重復識別后,利用識別的最優模型參數計算應變激勵幅值為0.1,0.5和1.0時的應變-應力遲滯回線如圖6所示,適應度的均值收斂曲線如圖7所示。
從圖6可以看出,本發明能夠準確識別粘彈阻尼器滯彈位移場模型的參數,計算得到不同激勵幅值下的粘彈阻尼器應變-應力遲滯回線同試驗值非常吻合。從圖7可以看出,對于粘彈阻尼器滯彈位移場模型的參數識別問題,相比于標準粒子群算法,本發明能夠更準確、快速地收斂于最優解,具有比標準粒子群算法更好的收斂性能。
以上所述僅是本發明的優選實施方式,應當指出,對于本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以做出若干改進和潤飾,這些改進和潤飾也應視為本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!