一種改進的光滑自由變形算法的制作方法
本發明涉及計算機圖像處理技術領域,具體地說,涉及一種改進的光滑自由變形算法。
背景技術:
在幾何建模和計算機動畫中,空間變形是幾何外形編輯和柔性體動畫生成的關鍵技術之一,其中,最具代表性的是自由變形技術(ffd),已發展出多個變種,如精確自由變形方法、光滑自由變形方法等,由于其簡單易用、功能強大,已經被集成到3dsmax、maya、softimagexsi等商業軟件中。
由于傳統自由變形方法的變形是作用到待編輯模型的采樣點上,再由采樣點變形后的位置還原出模型的變形結果,導致其在變形過程中存在因采樣點密度太小而出現走樣的問題。
為解決走樣問題,通常是增加采樣點的密度,但會造成性能上較大的開銷;更進一步的方法是根據面片大小和曲面曲率,自適應確定采樣密度,雖然降低了性能開銷,但自適應算法實現相對復雜,且無法很好地處理一些奇異情況。
精確自由變形作為解決ffd中走樣問題的方法,其是通過沿節點盒切割初始三角面片,計算三角面片上足夠數目采樣點變形后的位置,再用采樣點插值計算出原始三角面片變形后的精確結果。
光滑自由變形方法通過以下六步驟對精確自由變形方法進行改進:
(1)定義變形空間步驟
選用b樣條體作為變形空間,記作r(μ,ν,ω):
其中,
然后用該變形空間包裹待變形模型。
(2)三角剖分步驟
通過b樣條體上的節點盒分割初始三角面片。
(3)模型嵌入步驟
在本步驟中,嵌入過程為計算待變形模型在變形空間中參數坐標的過程,具體通過嵌入函數u=e(x)將采樣點從世界坐標系映射到變形空間,其中,x為采樣點在世界坐標系中的坐標,u為采樣點在變形空間中的參數坐標。
嵌入函數e由變形空間決定,在光滑自由變形中,通常是通過一定方法構造b樣條體,使嵌入變形空間點的參數坐標與該點在世界坐標系中的坐標相等,即e(x)=x,以簡化嵌入過程中的計算。
并通常選用三次貝塞爾曲面片來擬合精確的變形結果,由于每一個切割產生的三角形,都會在變形后得到一個三角貝賽爾曲面片,所以要在每一個切割產生的三角形上進行采樣,共需要3×3個約束點及m(m由變形空間的次數決定)個擬合點,即光滑自由變形共需要9+m個采樣點。
然后用e(x)=x計算出采樣點在變形空間中的參數坐標,同時通過重心坐標插值計算采樣點的法向。
(4)幾何變形步驟
幾何變形過程為改變變形空間并將該變形傳遞至待變形模型的過程,具體為將采樣點嵌入b樣條體中,以通過這些采樣點將變形空間的變形傳遞至待變形模型中的。當用戶改變b樣條體控制頂點的位置后,先將采樣點的參數坐標和控制頂點位置代入到定義變形空間所用的公式中,以求得采樣點變形后的位置;再以這些新的位置為輸入,通過帶約束的擬合方法,求出作為變形結果的三角貝塞爾曲面的控制頂點。
(5)法向變形步驟
為了解決精確自由變形中結果不夠光滑自然的問題,通過重心坐標插值估算得采樣點的法向,然后計算出采樣點的法向量變形以后的值;接著,用與幾何變形步驟中相同的方法,以采樣點變形后的法向量為輸入,用三次貝塞爾曲面片擬合出變形后的三角曲面片法向量場。在細分階段同時細分法向量場,并以此作為細分三角形的法向,從而可得到在光滑邊兩側視覺上g1連續的幾何和g0連續的法向量場;在尖銳邊兩側g0連續的幾何和g-1連續的法向量場。
(6)幾何微調步驟
為了得到視覺上更加細膩的變形結果,還需根據法向信息對表示幾何的三角貝塞爾曲面片的控制頂點進行微調。
(7)細分繪制步驟
將法向變形步驟與幾何微調步驟中的結果進行細分后繪制。
經過上述七個步驟的處理后,通過將cuda應用到了精確自由變形中,不僅可實現比精確自由變形方法快50倍左右的計算速度,而且改進了變形結果的視覺美觀度。但是,在三角均勻剖分步驟中,其沿節點盒切割三角形,存在以下問題:(1)容易切割出狹長三角形和蛻化三角形,不僅會浪費計算資源,可能還會帶來浮點數計算錯誤,導致程序運行速度變慢,魯棒性變差;(2)通常切割產生的三角形越小,變形后的誤差也越小,但在該步驟中,切割成的三角形大小由節點盒分布和模型三角形分布決定,用戶難以控制切割結果,即,無法對模型變形后誤差的大小進行控制。
技術實現要素:
本發明的目的為提供一種改進的光滑自由變形算法,以解決現有光滑自由變形算法中三角剖分步驟中存在的問題,以使光滑自由變形更加魯棒高效。
為了實現上述目的,本發明提供的光滑自由變形算法包括三角均勻剖分步驟;三角均勻剖分步驟包括:
步驟1,獲取初始三角面片;
步驟2,依據等分段長度控制參數,對初始三角面片最小內角的兩邊進行等分;
步驟3,連接鄰近最小內角頂點的兩個等分點,形成頂三角形與待剖分四邊形;
步驟4,以待剖分四邊形與頂三角形共有的端點為起點,對應連接待剖分四邊形上的等分點,剖分成若干個類梯形;
步驟5,依據等分段長度控制參數,對類梯形頂邊與底邊進行等分,并連接等分點對類梯形進行三角剖分;若最小內角兩邊上的等分點數不等,則重復步驟4與步驟5,以距離最小內角頂點最遠的類梯形為待剖分四邊形進行三角剖分,且以位于最小內角等分點數較少的邊上的頂點為起點。
在上述三角均勻剖分步驟中,利用等分段長度控制參數,使切割產生的子三角形的邊長接近等分段長度控制參數,即分割產生的子三角形較接近正三角形,有效避免了狹長三角形或蛻化三角形的產生,使光滑自由變形過程更加魯棒高效。
一個具體的方案為依據等分段長度控制參數對邊進行等分的步驟包括:依據等分段數對邊進行等分,等分段數為邊長度與等分段長度控制參數之商的向上取整值。算法簡單。
另一個的具體方案為步驟2包括:接收對等分段長度控制參數的設定。通過接收用戶對等分段長度控制參數的設置,便于用戶對分割產生子三角形的大小進行控制,以根據需求和硬件的性能,對變形誤差進行控制。
另一個具體方案為步驟2包括:根據初始三角面片的頂點坐標,計算最小內角兩邊的長度;計算最小內角兩邊的等分段數,等分段數為邊長度與等分段長度控制參數之商的向上取整值;依據兩邊的端點坐標,計算等分點的坐標。
另一個具體的方案,步驟1包括:從文件中讀取待變形模型;對待變形模型進行三角化,形成初始三角面片。
另一個具體的方案,步驟2包括:根據初始三角面片的頂點坐標,計算各邊長度,最小內角為與最短邊相對的內角。
另一個具體的方案,連接等分點對類梯形進行三角剖分的步驟包括:沿同一連接方向,連接類梯形上底與下底上對應等分點,形成若干四邊形,并連接短對角線對四邊形進行剖分。
優選的方案為還包括步驟6:采用cvt優化方法對剖分結果進行優化。可使分割結果更加均勻。
進一步的優選方案,對剖分結果進行5次cvt優化。更好地平衡優化效果與計算開銷。
與現有的方法相比,本發明的有益效果在于:
(1)算法中不包含平面求交,更加高效、魯棒。
(2)剖分出的子三角形接近正三角形且面積接近相等,不會產生新的狹長或蛻化的三角形。
附圖說明
圖1為本發明實施例的工作流程圖;
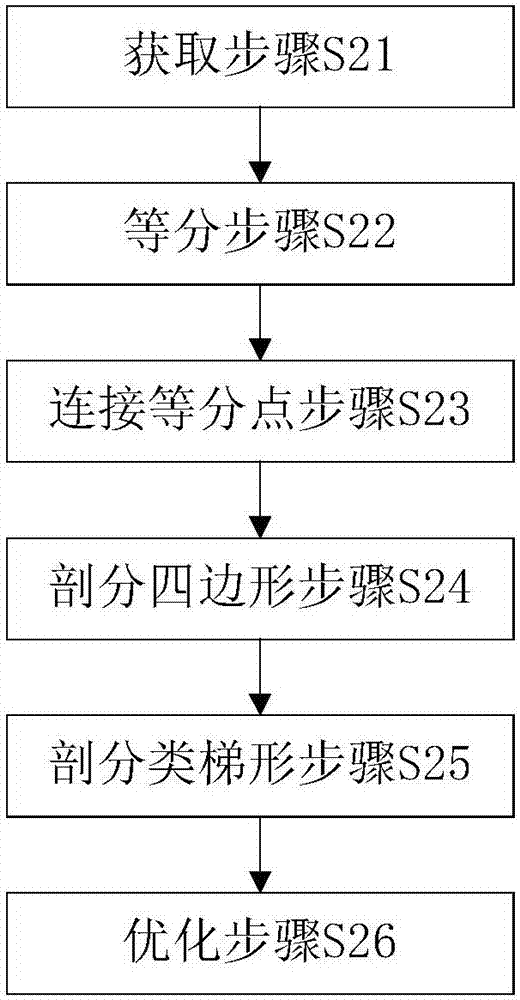
圖2為本發明實施例中三角均勻剖分步驟的工作流程圖;
圖3為本發明實施例中三角均勻剖分步驟的部分過程示意圖,其中(a)為初始三角面片,(b)為查找出初始三角面片的最小內角,(c)為對最小內角兩邊進行等分,(d)為剖分出的頂三角形,(e)為第一個待剖分的類梯形,(f)為對第一個類梯形上下底進行等分。
圖4為本發明實施例中三角均勻剖分步驟的其他部分過程示意圖,(a)為對第一個類梯形進行三角剖分,(b)為對第二個類梯形進行三角剖分,(c)為最后一個待剖分的類梯形,(d)為對最后一個類梯形進行部分三角剖分,(e)為三角剖分結果,(f)為對剖分結果進行cvt優化。
具體實施方式
以下結合實施例及其附圖對本發明作進一步說明。
實施例
參見圖1,本發明改進的光滑自由變形算法包括定義變形空間步驟s1、三角均勻剖分步驟s2、模型嵌入步驟s3、幾何變形步驟s4、法向變形步驟s5、幾何微調步驟s6及細分繪制步驟s7。
定義變形空間步驟s1,定義一個b樣條體作為包裹待變形模型的變形空間。
三角均勻剖分步驟s2,用三角均勻剖分算法將待變形模型中的初始三角面片分割成若干個子三角形,以減小變形后的誤差。
參見圖2,三角均勻剖分步驟s2包括獲取步驟s21、等分步驟s22、連接等分點步驟s23、剖分四邊形步驟s24、剖分類梯形步驟s25及優化步驟s26。
獲取步驟s21,獲取初始三角面片。
從文件中讀取待變形模型;
對待變形模型進行三角化,形成如圖3(a)所示的初始三角面片1。
等分步驟s22,依據等分段長度控制參數l,對初始三角面片最小內角的兩邊進行等分。
接收對等分段長度控制參數l的設定,用戶根據初始三角面片尺寸及其對精度的要求,通過輸入界面對控制參數l進行設定,使用戶能夠更好地控制變形誤差。
如圖3(b)所示,根據初始三角面片1的頂點坐標,計算其邊11、邊12及邊13的長度,然后采用排序法對三邊長度進行升序排列,其中位于第一位的邊13所對的角α為初始三角面片1的最小內角。
計算最小內角的邊11與邊12的長度;依據等分段長度控制參數l,計算邊11與邊12的等分段數,其中,等分段數為邊長度與等分段長度控制參數l之商的向上取整值,即邊11與邊12的等分段數分別為
依據邊11與邊12的端點坐標,計算等分點坐標,對于最小內角具體的一邊,例如邊11,設其兩個端點的坐標為p1,p2,則
連接等分點步驟s23,參見圖3(d),連接鄰近最小內角頂點的兩個等分點,形成頂三角形2與待剖分四邊形3。
剖分四邊形步驟s24,如圖3(d)所示,以待剖分四邊形3與頂三角形2共有的端點為起點,對應連接待剖分四邊形3上的等分點,剖分成若干個類梯形,如圖3(e)的實線部分為第一個類梯形31。
剖分類梯形步驟s25,以如圖3(e)所示的第一個類梯形31為例,依據等分段長度控制參數l,對第一個類梯形31的上底與下底進行等分,結果如圖3(f)所示;沿同一連接方向,比如由圖中的左向右,將對應連接上底與下底等分點形成的四邊形用其短對角線進行剖分,結果如圖4(a)所示。
從上至下,依序對各個類梯形進行三角剖分,在剖分過程中,如圖4(b)所示,第二個類梯形32上底與下底的等分段數相等,連接其上底與下底上對應等分點,形成若干四邊形,根據四邊形的四個頂點計算其兩條對角線的長度,沿著較短的那條對角線分割四邊形,最終使每個四邊形分割成兩個三角形。
如圖4(c)所示,第三個類梯形33的上底分割段數比下底少1,對上底和下底的均分點進行編號,上底的編號從左到右為1到k,下底的編號從左到右為1到k+1,在第三個類梯形33上,先連接上下底編號相同的點。除此之外,對于上底中的每個點,若其編號為j,則使將其與下底中編號為j+1的點相連,最終將第三個類梯形33分割成多個鋸齒狀的三角形。
若最小內角兩邊上的等分點數不等,如圖4(c)、圖4(d)所示,重復步驟s24與步驟s25,以距離最小內角頂點最遠的類梯形34為待剖分四邊形進行三角剖分,且以位于最小內角等分點數較少的邊上的頂點為起點。將距離最小內角頂點最遠的類梯形33逆時針旋轉90度,使該類梯形33和圖3中待剖分四邊形3類似,延長該類梯形33的上底和下底,相交后與最小內角的另一條邊的剩余部分構成一個三角形,把該三角形當作如圖3(a)所示的原始三角面片,并對其執行步驟s22至步驟s25,在剖分過程,初始三角面片1被分割成如圖4(d)所示,直至三角面片1剖分成如圖4(e)所示。
優化步驟s26,如圖4(f)所示,采用cvt優化方法對初始三角面片1剖分結果進行優化,并對該結果進行5次cvt優化,使子三角形更加均勻。cvt優化方法為duq,faberv,gunzburgerm.centroidalvoronoitessellations:applicationsandalgorithms[j].siamreview,1999,41(4):637–676中介紹的方法。
模型嵌入步驟s3,將模型嵌入變形空間,計算剖分后產生的每個三角面片的采樣點在變形空間中的參數坐標和法向。
幾何變形步驟s4,用戶改變變形空間的控制頂點,對變形空間進行變形。保持采樣點在變形空間中參數坐標不變,計算采樣點在世界坐標系下的新的位置,根據得到變形后的采樣點,用帶約束的擬合方法計算出每個三角面片變形后的結果,該結果用三角貝塞爾曲面片表示。
法向變形步驟s5,計算采樣點在世界坐標系下的新的法向,根據得到變形后的采樣點的法向,用帶約束的擬合方法計算出每個三角面片變形后的法向量場,該結果用三角貝塞爾曲面片表示。
幾何微調步驟s6,調整幾何變形步驟s4得到的三角貝塞爾曲面片的控制頂點,使變形結果更加光滑自然。
細分繪制步驟s7,將法向變形步驟s5與幾何微調步驟s6中的結果進行細分后繪制。
- 還沒有人留言評論。精彩留言會獲得點贊!