高強度兩級漸變剛度板簧的剛度特性的計算方法與流程

本發明涉及車輛懸架板簧，特別是高強度兩級漸變剛度板簧的剛度特性的計算方法。

背景技術：

隨著高強度鋼板材料的出現，可采用高強度兩級漸變剛度板簧，進一步滿足在不同載荷下的懸架漸變偏頻保持不變的設計要求。高強度兩級漸變剛度板簧的剛度特性，影響車輛行駛平順性和安全性，它不僅與高強度兩級漸變剛度板簧的主簧各片和副簧的結構有關，而且還與第1第和第2次開始接觸載荷及第2次完全接觸載荷有關，同時，由于主簧和第一級副簧及與第二級副簧在漸變過程中的撓度及漸變剛度計算非常復雜，據所查資料可知，目前國內外尚未給出高強度等二級漸變剛度板簧的剛度特性的計算方法。隨著車輛行駛速度及其對平順性要求的不斷提高，對高強度兩級漸變剛度板簧懸架系統設計提出了更高要求，因此，必須建立一種精確、可靠的高強度兩級漸變剛度板簧的剛度特性的計算方法，確保高強度兩級漸變剛度板簧的剛度特性滿足車輛懸架系統的設計要求，提高高強度兩級漸變剛度板簧的設計水平、產品質量和性能，滿足車輛行駛平順性和安全性的設計要求；同時，降低設計及試驗費用，加快產品開發速度。

技術實現要素：

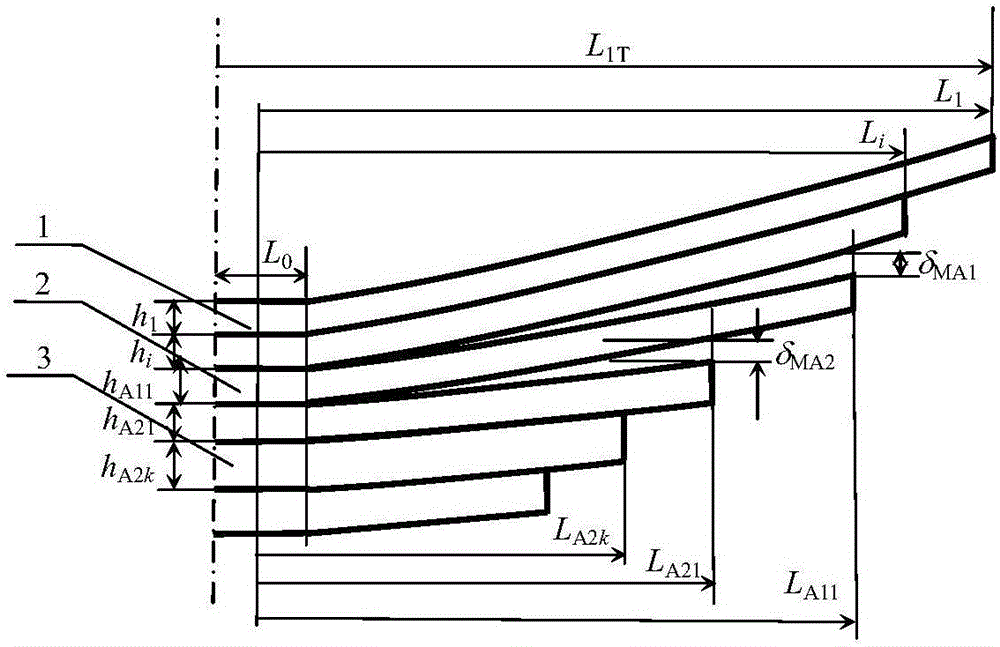
針對上述現有技術中存在的缺陷，本發明所要解決的技術問題是提供一種簡便、可靠的高強度兩級漸變剛度板簧的剛度特性的計算方法，設計流程圖，如圖1所示。板簧采用高強度鋼板，寬度為b，彈性模量為E，各片板簧為以中心穿裝孔對稱的結構，安裝夾緊距的一半L₀為騎馬螺栓夾緊距的一半L₀；高強度等偏頻兩級漸變剛度板簧的一半對稱結構如圖2所示，由主簧1、第一級副簧2和第二級副簧3構成，其中，主簧1的片數為n，主簧各片的厚度為h_i，一半作用長度為L_iT，一半夾緊長度為L_i＝L_iT-L₀/2，i＝1,2,…,n，主簧夾緊剛度為K_M。第一級副簧2的片數為m₁，第一級副簧各片的厚度為h_A1j，一半作用長度為L_A1jT，一半夾緊長度為L_A1j＝L_AjT-L₀/2，j＝1,2,…,m₁，主簧與第一級副簧的復合夾緊剛度為K_M1，末片主簧的下表面與第一副簧首片的上表面之間的設置有第一級漸變間隙δ_MA1。第二級副簧3的片數為m₂，第二級副簧各片的厚度為h_A2k，一半作用長度為L_A2kT，一半夾緊長度為L_A2k＝L_A2kT-L₀/2，k＝1,2,…,m₂，主簧與第一級和第二級副簧的總復合夾緊剛度為K_MA2，第一級副簧末片下表面與第二副簧首片的上表面之間的設置有第二級漸變間隙δ_MA2。當載荷P小于第1次開始起作用載荷P_k1時，只有主簧起作用，懸架夾緊剛度為主簧夾緊剛度K_M；當載荷達到第2次開始起作用載荷P_k2時，末片主簧下表面與第一級副簧首片上表面完全接觸，板簧夾緊剛度為主簧和第一級副簧的復合夾緊剛度K_MA1；當載荷達到第2次完全起作用載荷P_w2時，主簧和第一級副簧與第二級副簧完全接觸，懸架夾緊剛度為主副簧的總復合夾緊剛度K_MA2。當載荷在[P_k1,P_w2]范圍內變化時，高強度兩級漸變剛度板簧的第一級和第二級漸變復合夾緊剛度K_kwP1和K_kwP2隨載荷而變化，從而滿足在不同載荷下的懸架系統偏頻保持不變的設計要求。根據各片板簧的結構參數，彈性模量，接觸載荷，空載載荷和額定載荷，對高強度兩級漸變剛度板簧在不同載荷下的夾緊剛度特性進行計算。

為解決上述技術問題，本發明所提供的高強度兩級漸變剛度板簧的剛度特性的計算方法，其特征在于采用以下匹配設計步驟：

(1)高強度兩級漸變剛度板簧的各不同片數l重疊段的等效厚度h_le的計算：

根據主簧的片數n，主簧各片的厚度h_i，i＝1,2,…,n；第一級副簧的片數m₁，第一級副簧各片的厚度h_A1j，j＝1,2,…,m₁；第二級副簧的片數m₂，第二級副簧各片的厚度h_A2k，j＝1,2,…,m₂；主簧的總片數N＝n+m₁+m₂，對高強度兩級漸變剛度板簧的各不同片數l重疊段的等效厚度h_le進行計算，l＝1,2,…,N，即

(2)高強度兩級漸變剛度板簧的主簧夾緊剛度K_M的計算：

根據高強度兩級漸變剛度板簧的寬度b，彈性模量E；主簧的片數n，主簧各片的一半夾緊長度L_i，及步驟(1)中計算得到的h_le，l＝i＝1,2,…,n，對高強度兩級漸變剛度板簧的主簧夾緊剛度K_M進行計算，即

(3)高強度兩級漸變剛度板簧的主簧與第一級副簧復合夾緊剛度K_MA1的計算：

根據高強度兩級漸變剛度板簧的寬度b，彈性模量E；主簧的片數n,主簧各片的一半夾緊長度L_i，i＝1,2,…,n；第一級副簧的片數m₁，第一級副簧各片的一半夾緊長度L_A1j＝L_n+j，j＝1,2,…,m₁，主簧與第一級副簧的片數之和N₁＝n+m₁，及步驟(1)中計算得到的h_le，l＝1,2,…,N₁，對主簧與第一級副簧的復合夾緊剛度K_MA1進行計算，即

(4)高強度兩級漸變剛度板簧的主副簧總復合夾緊剛度K_MA2的計算：

根據高強度兩級漸變剛度板簧的寬度b，彈性模量E；主簧的片數n，主簧各片的一半夾緊長度L_i，i＝1,2,…,n；第一級副簧的片數m₁，第一級副簧各片的一半夾緊長度L_A1j＝L_n+j，j＝1,2,…,m₁；第二級副簧的片數m₂，第二級副簧各片的一半夾緊長度分別為L_A2k＝L_N1+k，k＝1,2,…,m₂；主副簧的總片數N＝n+m₁+m₂，及步驟(1)中計算得到的h_le，l＝1,2,…,N，對主副簧的總復合夾緊剛度K_MA2進行計算，即

(5)高強度兩級漸變剛度板簧的第一級和第二級漸變夾緊剛度K_kwP1和K_kwP2的計算：

I步驟：第一級漸變夾緊剛度K_kwP1的計算

根據第1次開始接觸載荷P_k1，第2次開始接觸載荷P_k2，步驟(2)中計算得到的K_M，對載荷P在[P_k1，P_k2]范圍時的第一級漸變夾緊剛度K_kwP1進行計算，即

II步驟：第二級漸變夾緊剛度K_kwP2的計算

根據第2次開始接觸載荷P_k2，第2次完全接觸載荷P_w2，步驟(3)中計算得到的K_MA1，對載荷P在[P_k2，P_w2]范圍時的第二級漸變夾緊剛度K_kwP2進行計算，即

(6)高強度兩級漸變剛度板簧的夾緊剛度隨載荷變化特性的計算：

根據空載載荷P₀，額定載荷P_N第1次開始接觸載荷P_k1，第2次開始接觸載荷P_k2，第2次完全接觸載荷P_w2，步驟(2)中計算得到的K_M，步驟(3)中計算得到的K_MA1，步驟(4)中計算得到的K_MA2，步驟(5)中計算得到的K_kwP1和K_kwP2，對高強度兩級漸變剛度板簧在不同載荷P下的夾緊剛度特性K_P進行計算，即

本發明比現有技術具有的優點

主簧與一級副簧和二級副簧的漸變接觸過程中，高強度等偏頻兩級漸變剛度板簧的撓度和漸變夾緊復合剛度計算非常復雜，不僅與主簧和一級副簧及二級副簧的結構參數有關，而且還與接觸載荷有關，據所查資料可知，先前國內外一直未給出高強度兩級漸變剛度板簧的剛度特性的計算方法。本發明可根據高強度兩級漸變剛度板簧的主簧各片和副簧的結構參數，彈性模量，空載載荷、額定載荷、第1第開始接觸載荷P_k1、第2次開始接觸載荷P_k2和完全接觸載荷P_w2，對高強度兩級漸變剛度板簧的夾緊剛度隨載荷的變化特性進行計算。通過ANSYS仿真和樣機試驗驗證可知，本發明所提供的高強度兩級漸變剛度板簧的剛度特性的計算方法是正確的。利用該方法可得可靠的剛度特性設計值，確保剛度特性滿足懸架系統的設計要求，提高車輛行駛平順性和安全性；同時，還可降低設計和試驗費用，加快產品開發速度。

附圖說明

為了更好地理解本發明，下面結合附圖做進一步的說明。

圖1是高強度兩級漸變剛度板簧的剛度特性的計算流程圖；

圖2是高強度兩級漸變剛度板簧的一半對稱結構示意圖；

圖3是實施例的主簧ANSYS變形仿真云圖；

圖4是實施例的主簧和第一級副簧的ANSYS變形仿真云圖；

圖5是實施例的主副簧的ANSYS變形仿真云圖；

圖6是實施例的第一級漸變夾緊剛度K_kwP1隨載荷P的變化曲線；

圖7是實施例的第二級漸變夾緊剛度K_kwP2隨載荷P的變化曲線；

圖8是實施例的高強度兩級漸變剛度板簧的夾緊剛度K_P隨載荷P的變化曲線。

具體實施方案

下面通過實施例對本發明作進一步詳細說明。

實施例：某高強度兩級漸變剛度板簧的寬度b＝63mm，騎馬螺栓夾緊距的一半L₀＝50mm，彈性模量E＝200GPa，許用應力[σ]＝430MPa。主簧片數n＝2，主簧各片的厚度h₁＝h₂＝8mm，主簧各片的一半作用長度分別為L_1T＝525mm，L_2T＝450mm；主簧各片的一半夾緊長度分別為L₁＝L_1T-L₀/2＝500mm，L₂＝L_2T-L₀/2＝425mm。第一級副簧的片數m₁＝1，厚度h_A1j＝11mm，一半作用長度為L_A11T＝360mm，一半夾緊長度L_A11＝L₃＝L_A11T-L₀/2＝335mm。第二級副簧的片數m₂＝2，第二級副簧各片的厚度h_A21＝11mm，h_A22＝11mm，一半作用長度分別為L_A21T＝250mm，L_A22T＝155mm；一半夾緊長度分別L_A21＝L₄＝L_A21T-L₀/2＝225mm，L_A22＝L₅＝L_A22T-L₀/2＝130mm。主副簧的總片數N＝n+m₁+m₂＝5。空載載荷P₀＝1715N，額定載荷P_N＝7227N；第1次開始接觸載荷P_k1＝1888N，第2次開始接觸載荷P_k2＝2641N，第2次完全接觸載荷P_w2＝3694.2N。根據各片板簧的結構參數，彈性模量，接觸載荷、空載載荷和額定載荷，對該高強度兩級漸變剛度板簧的夾緊剛度隨載荷變化特性進行計算。

本發明實例所提供的高強度兩級漸變剛度板簧的剛度特性的計算方法，其計算流程如圖1所示，具體計算步驟如下：

(1)高強度兩級漸變剛度板簧的各不同片數l重疊段的等效厚度h_le的計算：

根據主簧的片數n＝2，主簧各片的厚度h₁＝h₂＝8mm；第一級副簧的片數m₁＝1,厚度h_A11＝11mm；第二級副簧的片數m₂＝2,第二級副簧各片的厚度h_A21＝11mm；h_A22＝11mm；主副簧的總片數N＝5，對漸變剛度板簧各不同片數重疊段的等效厚度h_le進行計算，l＝1,2,…,N，即

h_1e＝h₁＝8.0mm；

(2)高強度兩級漸變剛度板簧的主簧夾緊剛度K_M的計算：

根據高強度兩級漸變剛度板簧的寬度b＝63mm，彈性模量E＝200GPa；主簧片數n＝2，主簧各片的一半夾緊長度L₁＝500mm，L₂＝425mm，及步驟(1)中計算得到的h_1e＝8.0mm，h_2e＝10.1mm，對主簧夾緊剛度進行計算，即

根據主簧各片的厚度、寬度和一半夾緊長度，彈性模量E，建立ANSYS仿真模型，在端部施加一集中力F＝900N，進行ANSYS變形仿真和剛度驗證，仿真得到的主簧ANSYS變形仿真云圖，如圖3所示，其中，端部最大撓度f_Mmax＝34.615mm，因此，高強度兩級漸變剛度板簧的主簧夾緊剛度ANSYS仿真驗證值K_M＝2F/f_Mmax＝52N/mm,與計算值K_M＝51.44N/mm的相對偏差僅為1.09％，結果表明高強度兩級漸變剛度板簧的主簧夾緊剛度K_M的計算值是準確可靠的。

(3)高強度兩級漸變剛度板簧的主簧與第一級副簧復合夾緊剛度K_MA1的計算：

根據高強度兩級漸變剛度板簧的寬度b＝63mm，彈性模量E＝200GPa；主簧的片數n＝2，主簧各片的一半夾緊長度L₁＝500mm，L₂＝425mm；第一級副簧的片數m₁＝1，一半夾緊長度L_A11＝L₃＝335mm，主簧與第一級副簧的片數之和N₁＝n+m₁＝3，及步驟(1)中計算得到的h_1e＝8.0mm，h_2e＝10.1mm，h_3e＝13.3mm，對主簧與第一級副簧的復合夾緊剛度K_MA1進行計算，即

根據主簧各片和第一級副簧的厚度、寬度和一半夾緊長度，彈性模量E，建立ANSYS仿真模型，在端部施加一集中力F＝2000N，進行ANSYS變形仿真和剛度驗證，仿真得到的ANSYS變形仿真云圖，如圖4所示，其中，端部最大撓度f_MA1max＝35.555mm，因此，高強度兩級漸變剛度板簧的主簧和第一級副簧的復合夾緊剛度ANSYS仿真驗證值K_MA1＝2F/f_MA1max＝112.502N/mm,與計算值K_MA1＝112.56N/mm的相對偏差僅為0.051％，表明高強度兩級漸變剛度板簧的主簧與第一副簧的復合夾緊剛度K_MA1的計算值是準確可靠的。

(4)高強度兩級漸變剛度板簧的主副簧總復合夾緊剛度K_MA2的計算：

根據高強度兩級漸變剛度板簧的寬度b＝63mm，彈性模量E＝200GPa；主簧的片數n＝2，主簧各片的一半夾緊長度L₁＝500mm，L₂＝425mm；第一級副簧片數m₁＝1，一半夾緊長度L_A11＝L₃＝335mm；第二級副簧片數m₂＝2，各片的一半夾緊長度分別為L_A21＝L₄＝225mm，L_A22＝L₅＝130mm。主副簧的總片數N＝5，及步驟(1)中計算得到的h_1e＝8.0mm，h_2e＝10.1mm，h_3e＝13.3mm，h_4e＝15.4mm；h_5e＝17.1mm；對主副簧的總復合夾緊剛度K_MA2進行計算，即

根據主簧和第一級副簧和第二級副簧的各片的厚度、寬度和一半夾緊長度，彈性模量E，建立ANSYS仿真模型，在端點施加一集中力F＝4000N，進行ANSYS變形仿真和剛度驗證，仿真得到的ANSYS變形仿真云圖，如圖5所示，其中，端部最大撓度f_MA2max＝44.184mm，因此，高強度兩級漸變剛度板簧的主副簧的復合夾緊剛度ANSYS仿真驗證值K_MA2＝2F/f_MA2max＝181.06N/mm,與計算值K_MA1＝181.86N/mm的相對偏差僅為0.44％，結果表明高強度兩級漸變剛度板簧的主副簧的復合夾緊剛度K_MA2的計算值是準確可靠的。

(5)高強度兩級漸變剛度板簧的第一級和第二級漸變夾緊剛度K_kwP1和K_kwP2的計算：

I步驟：第一級漸變夾緊剛度K_kwP1的計算

根據第1次開始接觸載荷P_k1＝1888N，第2次開始接觸載荷P_k2＝4133N，步驟(2)中計算得到的K_M＝51.44N/mm，對載荷P在[P_k1，P_k2]范圍時的該高強度兩級漸變剛度板簧的第一級漸變夾緊剛度K_kwP1進行計算，即

計算所得到的第一級漸變夾緊剛度K_kwP1隨載荷P的變化曲線，如圖6所示；其中，當載荷P＝P_k1＝1888N時的第一級漸變夾緊剛度K_kwP1＝K_M＝51.44N/mm，當載荷P＝P_k2＝4133N時的第一級漸變夾緊剛度K_kwP1＝K_MA1＝112.56N/mm。

II步驟：第二級漸變夾緊剛度K_kwP2的計算

根據第2次開始接觸載荷P_k2＝4133N，第2次完全接觸載荷P_w2＝6678N，步驟(3)中計算得到的K_MA1＝112.56N/mm，對載荷P在[P_k2，P_w2]范圍時的該高強度兩級漸變剛度板簧的第二級漸變夾緊剛度K_kwP2進行計算，即

計算所得到的第二級漸變夾緊剛度K_kwP2隨載荷P的變化曲線，如圖7所示；其中，當載荷P＝P_k2時的第二級漸變夾緊剛度K_kwP2＝K_MA1＝112.56N/mm；當載荷P＝P_w2時的第二級漸變夾緊剛度K_kwP2＝K_MA2＝181.86N/mm。

(6)高強度兩級漸變剛度板簧的夾緊剛度隨載荷變化特性的計算：

根據空載載荷P₀＝1715N，額定載荷P_N＝7227N,第1次開始接觸載荷P_k1＝1888N，第2次開始接觸載荷P_k2＝4133N，第2次完全接觸載荷P_w2＝6678N，步驟(2)中計算得到的K_M＝51.44N/mm，步驟(3)中計算得到的K_MA1＝112.56N/mm，步驟(4)中計算得到的K_MA2＝181.86N/mm，步驟(5)中計算得到的K_kwP1和K_kwP2，對該高強度兩級漸變剛度板簧在不同載荷P下的夾緊剛度特性進行計算，即

利用Matlab計算程序，計算所得到的該高強度兩級漸變剛度板簧的夾緊剛度K_P隨載荷P的變化曲線，如圖8所示。

通過ANSYS仿真和樣機加載變形試驗測試可知，本發明所提高的高強度兩級漸變剛度板簧的剛度特性的計算方法是正確的，可得到高強度兩級漸變剛度板簧的剛度特性的計算值，為高強度兩級漸變剛度板簧的設計及CAD軟件開發奠定了可靠的技術基礎。利用該方法可提高高強度兩級漸變剛度板簧的設計水平、質量和性能，確保板簧漸變剛度特性滿足懸架系統的設計要求，提高車輛行駛平順性和安全性；同時，降低設計及試驗測試費用，加快產品開發速度。