基于協同進化和反向傳播的深度神經網絡優化方法與流程

本發明屬于深度學習與進化算法領域的結合，主要解決深度神經網絡的參數優化問題，具體提供一種基于協同進化和反向傳播的深度神經網絡優化方法，實現深度神經網絡參數的優化。

背景技術：

20世紀80年代以來，神經網絡(Neural Network,NN)進入了發展的快車道，新的科學理論的重大突破和高性能計算機的飛速發展使NN重煥生機。1982年加利福利亞理工學院的教授Hopfield提出了著名的Hopfield神經網絡模型，從而有力地推動了NN的研究。到了八十年代中期，Ackley，Hinton和Sejnowski，在Hopfield NN模型中基于模擬退火思想引入了隨機機制，并基于此模型分析了生物計算與傳統的AI計算之間的區別，提出了Boltzmann機，為NN優化計算跳出局部極小值提供了一個有效的方法，第一次成功實現了多層神經網絡的功能，并明確了NN中的隱單元的概念。第二年，反向傳播算法(Back-Propagation algorithm,BP)獲得進展，Rumelhart和McClelland提出的并行分布處理理論對反向傳播算法的應用產生了重要影響。這兩種模型或理論，對神經網絡的發展具有非常重要的作用和意義。

近些年來，神經科學研究人員發現，哺乳類動物的大腦皮質，在傳遞表示信息時，大腦皮質未曾對感官信號數據直接進行特征提取處理，接收到的刺激信號經過一個復雜的層狀神經元網絡時，呈現的特征會被逐層識別出來，然后每層的特征作為下一層的輸入信號，逐層進行處理后再次傳遞。人腦是根據經過聚集和分解處理后的外部世界感知信息對物體進行識別，這種感知系統的層次結構極大降低了神經系統的數據處理量，同時仍保留了有效的物體結構。而深度學習神經網絡系統，也是通過組合低層特征形成更加抽象的高層表示屬性類別或特征，最后得到數據的分布式特征表示的一種特殊網絡模型-深度神經網絡(Deep Neural Network,DNN)。DNN在很多領域都有著應用，例如：語音識別，文本圖像分類，天氣預測，人臉識別等等。

目前的深度神經網絡的優化算法，一種是：基于梯度的反向傳播算法，該算法隨著網絡結果和數據的復雜性的增加，容易陷入局部最優解；另一種是進化算法，由于參數維數的不斷增加，傳統的進化算法不再適用。

隨著數據規模的不斷增加，在處理這種大規模，無序的數據集時，人們越來越發現深度神經網絡的優勢，深度神經網絡必將有著更好的前景。

技術實現要素：

本發明的目的是克服上述已有技術的不足，提供一種基于協同進化和反向傳播的深度神經網絡優化方法，避免了反向傳播算法容易陷入局部最優解的缺陷，同時也利用反向傳播算法快速有效的優點，提高進化算法的搜索速度，通過一種迭代方式將這兩種方法的優點很好的結合到一起來優化深度神經網絡的參數。

為此，本發明提供了基于協同進化和反向傳播的深度神經網絡優化方法，包括如下步驟：

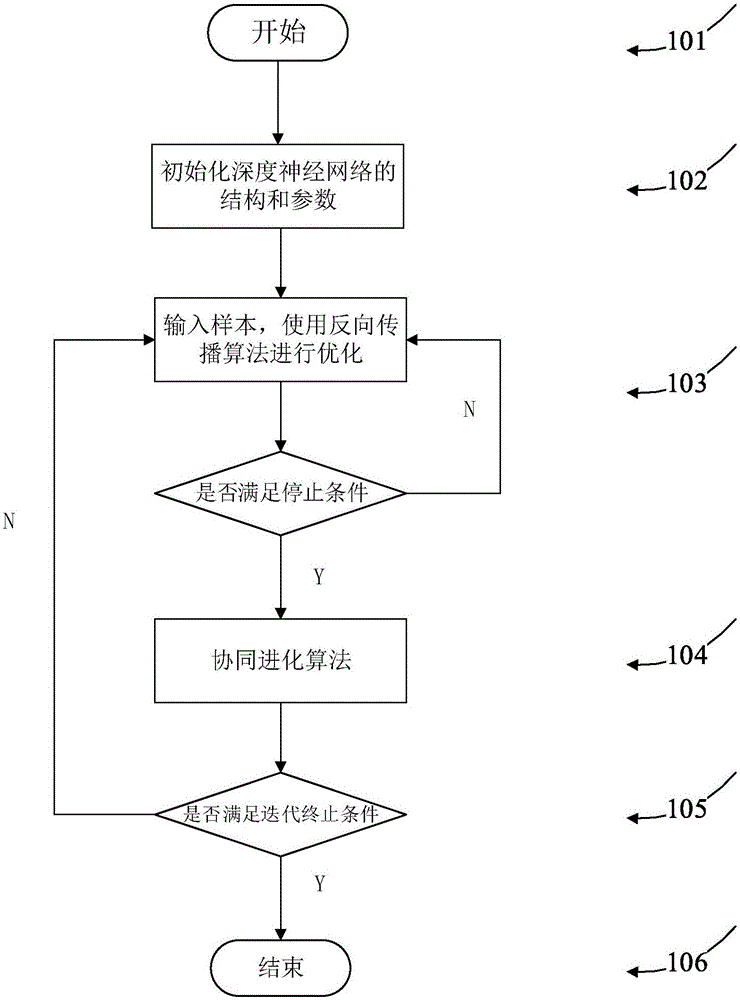
步驟101：開始基于協同進化和反向傳播的深度神經網絡優化方法；

步驟102：設定一個深度神經網絡結構，用L_i表示網絡的第i層，N_i表示第i層的節點個數，初始化權重W和偏差b，設置學習率η，自定義參數H；

步驟103：向步驟102的深度神經網絡輸入訓練樣本，然后使用反向傳播算法對深度神經網絡進行訓練，直到深度神經網絡連續兩次的迭代誤差變化值σ在范圍[0,H]內，停止反向傳播算法；

步驟104：采用協同進化算法對步驟103中采用反向傳播算法訓練的權重和偏差進行優化；

步驟105：采用協同進化算法優化完權重和偏差之后，繼續使用反向傳播算法進行優化，直到深度神經網絡連續兩次的迭代誤差變化值σ在范圍[0,H]內，停止反向傳播算法，再次使用協同進化算法進行優化，不停的進行迭代，最后直到迭代次數為50次，迭代終止；

步驟106：得到深度神經網絡的優化參數，即權重和偏差。

所述的步驟103，包括如下步驟：

步驟301：開始反向傳播算法；

步驟302：輸入訓練樣本到深度神經網絡，計算訓練樣本的誤差，根據誤差的梯度來反向調整深度神經網絡每一層的權重：

其中，W是調整前的權重，W′是調整后的權重，E是誤差，η是學習率；

步驟303：每次迭代，隨機選取D_s個樣本，根據步驟302中的權重調整公式來不斷更新權重；

步驟304：計算連續兩次迭代的誤差變化σ，當0≤σ≤H時，停止反向傳播算法的迭代過程；

步驟305：結束反向傳播算法。

所述的步驟104，包括如下步驟：

步驟401：開始使用協同進化算法對深度神經網絡進行優化；

步驟402：在反向傳播算法得到的權重基礎上，使用協同進化算法進行優化，將深度神經網絡按層按節點劃分為子問題；

步驟403：計算劃分后的每個子問題的成熟度M,并將這些成熟度按照從小到大的順序進行排序，選取成熟度排在前30％的子問題使用差分進化算法進行優化；

步驟404：采用差分進化算法優化完成之后，選取最優的解去替換步驟402的權重中相應位置的參數，直到所有被選取的子問題被優化完成；

步驟405：結束協同進化算法。

所述的步驟105，包括如下步驟：

步驟501：再次開始反向傳播算法；

步驟502：如果連續兩次的迭代誤差值σ在范圍[0,H]內，停止反向傳播算法，開始進行協同進化；

步驟503：按照步驟402將深度神經網絡按層按節點劃分為子問題，再按照步驟403進行子問題的選取，然后使用差分進化算法對這些子問題進行優化，選取最優的解來替換步驟502的權重中對應的參數；

步驟504：再次開始反向傳播算法，然后不斷的重復步驟502和步驟503，最后直到迭代次數為50次，迭代終止；

步驟505：結束基于協同進化和反向傳播的深度神經網絡優化方法。

所述的步驟103和步驟304中的誤差變化σ：

σ＝|E^(t)(x)-E^(t-1)(x)|

其中，E^(t)(x)和E^(t-1)(x)分別是第t次和第t-1次迭代的誤差。

所述步驟403中的成熟度M的定義：

其中，M_i是第i個子問題的成熟度，N是樣本的數量，表示第j個樣本在第i個子問題上的輸出，函數g(x)的定義如下：

其中，α是一個自適應參數，可以被設置成0.3或0.4。

本發明的有益效果：1、本發明是針對反向傳播算法在訓練參數的過程中容易陷入局部最優解的缺點，并且由于網絡的參數維數太大，單獨使用傳統的進化算法根本沒有辦法對其進行優化，因此提出了一種結合協同進化和反向傳播算法的方法來優化網絡，使得能夠更好的優化深度神經網絡的參數。

2、本發明將進化算法的優點應用到深度神經網絡的訓練中，針對大規模的參數，使用協同進化進行優化，同時結合反向傳播算法，并且設計一種選擇策略，來提高協同進化的優化速度，使得整個網絡能夠更高效的被訓練完成；

3、仿真結果表明，本發明采用的基于協同進化和反向傳播的深度神經網絡優化方法，優化性能好，提高了網絡的分類正確率。

以下將結合附圖對本發明做進一步詳細說明。

附圖說明

圖1是基于協同進化和反向傳播的深度神經網絡優化方法的主流程圖；

圖2是反向傳播算法(BP)的流程圖；

圖3協同進化的流程圖；

圖4是手寫數字識別數據集的一些樣例，每個小的數字圖片大小為28*28；

圖5是在神經網絡的結構：784-300-100-10時，反向傳播算法(BP)和本申請的方法(BP-CCDE)的比較，只進行一次協同進化，在迭代次數iter＝4時，開始進行協同進化，縱坐標表示average error，橫坐標表示迭代次數；

圖6是在神經網絡的結構：784-300-100-10時，反向傳播算法(BP)和本申請的方法(BP-CCDE)的比較，進行了兩次協同進化，在迭代次數iter＝4和iter＝19時，分別開始進行協同進化，縱坐標表示average error，橫坐標表示迭代次數。

圖7是在神經網絡的結構：784-500-300-10時，反向傳播算法(BP)和本申請的方法(BP-CCDE)的比較，只進行一次協同進化，在迭代次數iter＝12時，開始進行協同進化，縱坐標表示average error，橫坐標表示迭代次數；

圖8是在神經網絡的結構：784-500-300-10時，反向傳播算法(BP)和本申請的方法(BP-CCDE)的比較，進行了兩次協同進化，在迭代次數iter＝12和iter＝24時，分別開始進行協同進化，縱坐標表示average error，橫坐標表示迭代次數。

具體實施方式

下面結合附圖和實施例對本發明提供的基于協同進化和反向傳播的深度神經網絡優化方法進行詳細的說明。

本發明提出了一種基于協同進化和反向傳播的深度神經網絡優化方法，包括如下步驟：

步驟101：開始基于協同進化和反向傳播的深度神經網絡優化方法；

步驟102：設定一個深度神經網絡結構，用L_i表示網絡的第i層，N_i表示第i層的節點個數，初始化權重W和偏差b，設置學習率η，自定義參數H；

步驟103：向步驟102的深度神經網絡輸入訓練樣本，然后使用反向傳播算法對深度神經網絡進行訓練，直到深度神經網絡連續兩次的迭代誤差變化值σ在范圍[0,H]內，停止反向傳播算法；

步驟104：采用協同進化算法對步驟103中采用反向傳播算法訓練的權重和偏差進行優化；

步驟105：采用協同進化算法優化完權重和偏差之后，繼續使用反向傳播算法進行優化，直到深度神經網絡連續兩次的迭代誤差變化值σ在范圍[0,H]內，停止反向傳播算法，再次使用協同進化算法進行優化，不停的進行迭代，最后直到迭代次數為50次，迭代終止；

步驟106：得到深度神經網絡的優化參數，即權重和偏差。

所述的步驟103，包括如下步驟：

步驟301：開始反向傳播算法；

步驟302：輸入訓練樣本到深度神經網絡，計算訓練樣本的誤差，根據誤差的梯度來反向調整深度神經網絡每一層的權重：

其中，W是調整前的權重，W′是調整后的權重，E是誤差，η是學習率；

步驟303：每次迭代，隨機選取D_s個樣本，根據步驟302中的權重調整公式來不斷更新權重；

步驟304：計算連續兩次迭代的誤差變化σ，當0≤σ≤H時，停止反向傳播算法的迭代過程；

步驟305：結束反向傳播算法。

所述的步驟104，包括如下步驟：

步驟401：開始使用協同進化算法對深度神經網絡進行優化；

步驟402：在反向傳播算法得到的權重基礎上，使用協同進化算法進行優化，將深度神經網絡按層按節點劃分為子問題；

步驟403：計算劃分后的每個子問題的成熟度M,并將這些成熟度按照從小到大的順序進行排序，選取成熟度排在前30％的子問題使用差分進化算法進行優化；

步驟404：采用差分進化算法優化完成之后，選取最優的解去替換步驟402的權重中相應位置的參數，直到所有被選取的子問題被優化完成；

步驟405：結束協同進化算法。

所述的步驟105，包括如下步驟：

步驟501：再次開始反向傳播算法；

步驟502：如果連續兩次的迭代誤差值σ在范圍[0,H]內，停止反向傳播算法，開始進行協同進化；

步驟503：按照步驟402將深度神經網絡按層按節點劃分為子問題，再按照步驟403進行子問題的選取，然后使用差分進化算法對這些子問題進行優化，選取最優的解來替換步驟502的權重中對應的參數；

步驟504：再次開始反向傳播算法，然后不斷的重復步驟502和步驟503，最后直到迭代次數為50次，迭代終止；

步驟505：結束基于協同進化和反向傳播的深度神經網絡優化方法。

所述的步驟103和步驟304中的誤差變化σ：

σ＝|E^(t)(x)-E^(t-1)(x)|

其中，E^(t)(x)和E^(t-1)(x)分別是第t次和第t-1次迭代的誤差。

所述步驟403中的成熟度M的定義：

其中，M_i是第i個子問題的成熟度，N是樣本的數量，表示第j個樣本在第i個子問題上的輸出，函數g(x)的定義如下：

其中，α是一個自適應參數，可以被設置成0.3或0.4。

需要說明的是：反向傳播算法(英:Backpropagation algorithm，簡稱:BP算法)是一種監督學習算法，常被用來訓練多層感知機。反向傳播算法(BP算法)主要由兩個環節(激勵傳播、權重更新)反復循環迭代，直到網絡的對輸入的響應達到預定的目標范圍為止。差分進化算法是一種新興的進化計算技術，和其它演化算法一樣，DE(差分進化算法的外文縮寫)是一種模擬生物進化的隨機模型，通過反復迭代，使得那些適應環境的個體被保存了下來。但相比于進化算法，DE保留了基于種群的全局搜索策略，采用實數編碼、基于差分的簡單變異操作和一對一的競爭生存策略，降低了遺傳操作的復雜性。同時，DE特有的記憶能力使其可以動態跟蹤當前的搜索情況，以調整其搜索策略，具有較強的全局收斂能力和魯棒性，且不需要借助問題的特征信息，適于求解一些利用常規的數學規劃方法所無法求解的復雜環境中的優化問題。進化算法是一種成熟的具有高魯棒性和廣泛適用性的全局優化方法，具有自組織、自適應、自學習的特性，能夠不受問題性質的限制，有效地處理傳統優化算法難以解決的復雜問題。

以上三種算法都是現有的成熟的技術，其具體的定義和操作過程在此不作詳細的敘述。

本發明的效果可以通過以下仿真實驗進一步說明：

1、仿真參數

對于手寫數字識別數據集進行分析，可進行定量的結果分析：

①平均誤差：所有樣本的平均誤差，不同算法下的樣本誤差；

②分類正確率：測試樣本的正確分類的個數比上測試樣本的總的個數。

2、仿真內容

本發明方法首先對手寫數字識別數據集訓練，只使用反向傳播算法(BP)和本方法(BP-CCDE)進行比較，比較平均誤差和分類正確率。

3、仿真實驗結果及分析

手寫數字識別數據集如圖4所示，每個樣本的大小為28*28，訓練樣本一共60000個，測試集10000個，下面對兩種不同隱含層節點數的網絡進行驗證。

1.深度神經網絡的結構：784-300-100-10，含有兩個隱含層，在同樣的結構和初始化的條件下；通過BP和BP-CCDE的平均誤差結果如圖5所示，其中，實線和虛線分別表示BP和BP-CCDE方法隨著BP的迭代次數，平均誤差的變化；可見在加入協同進化之后，誤差有一個明顯的下降，圖5中在iter＝4時，開始使用協同進化。在圖6中，使用了兩次協同進化，平均誤差都有一個明顯的下降，分別是iter＝4和iter＝19時，可以看出引進協同進化之后，能夠使得誤差下降明顯。使用BP和BP-CCDE方法對手寫數字識別在不同的協同進化次數下的分類正確率如表1所示。

表1 BP和BP-CCDE方法對手寫數字識別的分類正確率

表1中BP的迭代次數iter＝50，K表示協同進化的使用次數；從表1中可以看出，在進行協同進化之后，本發明方法的分類正確率明顯高于BP算法。

2.深度神經網絡的結構：784-500-300-10，含有兩個隱含層，在同樣的結構和初始化的條件下；通過BP和BP-CCDE的平均誤差結果如圖7所示，其中，實線和虛線分別表示BP和BP-CCDE方法隨著BP的迭代次數，平均誤差的變化，圖7中在iter＝4時，開始使用協同進化。在圖8中，使用了兩次協同進化，平均誤差都有一個明顯的下降，分別是iter＝6和iter＝23時，使用協同進化。使用BP和BP-CCDE方法對手寫數字識別在不同的協同進化次數下的分類正確率如表2所示。

表2 BP和BP-CCDE方法對手寫數字識別的分類正確率

表2中BP的迭代次數iter＝50，K表示協同進化的使用次數；從表2中可以看出，在不同網絡結構下，在進行協同進化之后，本發明方法的分類正確率明顯高于BP算法。隨著協同進化方法的次數的增加，正確率也在不斷增加，可以看出本方法對于深度神經網絡的參數優化有著明顯的優勢。

以上例舉僅僅是對本發明的舉例說明，并不構成對本發明的保護范圍的限制，凡是與本發明相同或相似的設計均屬于本發明的保護范圍之內。本實施例沒有詳細敘述的部件和結構屬本行業的公知部件和常用結構或常用手段，這里不一一敘述。