結構量計算機的MSD乘法計算的方法與流程
本發明涉及計算機精密計算技術領域,具體涉及結構量計算機的MSD乘法計算的方法。
背景技術:
:
傳統電子計算機中的乘法運算面臨著計算精度低、延時長等問題。
乘法運算是最常用的基礎運算之一,廣泛應用于工程技術和科學計算的各個領域,是影響應用算法實現效率的關鍵路徑。長期以來,研究學者們致力于乘法的計算方法和實現過程的優化技術研究。在氣象預測、軍事通信、密碼學等應用領域里,隨著問題規模的不斷膨大,乘法運算面臨著響應速度緩慢、計算精度有限等問題。傳統電子計算機受到位數固定的電子處理器的制約,不能滿足設計高效乘法器的需要,超級計算機計算能力強大,但是伴隨著處理器數量的增加,大量計算資源消耗于通信和協調操作。于是人們開始關注各種新形式的計算機,而三值光學計算機是目前最接近實際應用的代表。
技術實現要素:
:
本發明所要解決的技術問題在于克服現有的技術缺陷提供一種方法合理、操作方便、計算精準的結構量計算機的MSD乘法計算的方法。
本發明所要解決的技術問題采用以下的技術方案來實現:
結構量計算機的MSD乘法計算的方法,其特征在于:包括以下步驟,
步驟一、表示數據:三值光學計算機采用改良符號數字系統(Modified Signed Digit,MSD)表示數據,即:n位的MSD數字A(an…ai…a1)和m位的B(bm…bj…b1)相乘,ai,bj∈{ī,0,1},運算關系表示為:
計算步驟為,
第1步:計算部分積Sj。將A與B的每一位形成的n位數據(bj…bj…bj)(j=1,2,...,m),送至M變換器上,實施M變換,得到Sj;
第2步:計算和數項Pj。為保證位數的對齊,將Sj高位附加m-j個零,末位附加j-1個零,得到Pj;
第3步:計算∑Pj。將相鄰奇偶和數項兩兩分組,送至三步式MSD加法器依次實施T與W、T'與W'及T2變換(真值表如圖1),得到的求和結果又稱為部分和,將作為下一輪加法器的輸入進行回饋運算,直到得到最終結果;
步驟二、并行加速算法:乘法算法是一個循環計算過程,乘法計算例程利用更多的光學處理器數據位數資源,構造出q個M變換器和r個MSD三步式加法器,將內部步驟盡可能作并行處理,用較少運算周期就可以快速獲得計算結果;
加速算法描述如下:第1步同時并行實施q組M變換,全部M變換運算分個批次完成;第2步可并行對Sj實施補零得到Pj;第3步,第次迭代時,相鄰P2j-1和分配到r個三步式加法器并行實施求和,全部求和分個批次完成;
步驟三、不對稱光路結構改良M變換:三值光學處理器由主光路和控制光路組成,結構上保持著不對稱性;
一次光運算是輸入光信號a和b,得到變換結果c的過程,其運算時間由公式
T=TSY+Tg+TCG+TLC+TC (2)
得到;
三態光發生器SY1和SY2將輸入信號編制成三態光,產生TSY;感光管g轉換三態光為電信號,產生Tg;電信號穿過重構電路CG的反應時間為TCG;CG產生的信號控制液晶LC改變旋光狀態,產生TLC;a依次穿過SY2、偏振片P2、LC、P3生成c,產生TC;在這5個時間里,Tg、TCG以及TLC與控制光路密切相關,并且TLC是最耗時的部分,約為其他部分的幾十倍以上。如果輸入b不變,從第二次運算開始,電信號、重構電路以及液晶狀態都保持不變,TSY+TC后就可以得到變 換結果c,可以縮減一半的處理器運算時間;乘法算法計算部分積時,每次都是將A(an…ai…a1)和(bj…bj…bj)送入M變換器,有一路輸入數據A始終保持不變,故可以合理分配數據A至控制光路,以縮短處理器計算延時;
步驟四、構造例程專用的結構量處理器:
Ⅰ按位分配數據位資源:用戶調用乘法例程時,輸入運算請求和原始數據A、B的同時,需要一并給出兩個乘法因子的數字位數n、m,作為分配數據位資源、構造結構量處理器的依據;
計算部分積時,n位的A(an…ai…a1)和(bj…bj…bj)實施M變換生成n位的Sj,需要M變換器的規模為:
VM=n (3)
Sj補零生成n+m-1位的Pj,對Pj進行二叉迭代求和時,每輪迭代輸出結果的數量會減半,根據三步式MSD加法器的運算規律可知,每輪迭代所需加法器的數據規模增加兩位,位數分析如圖5;
為避免重復構造運算器,以迭代過程中需要加法器的最多位數為準,故加法器的規模為:
三值邏輯變換器的每一位都要占用光學處理器的一個數據位,M變換器共計占用q×VM個數據位,一個VA位的三步式MSD加法器占用5VA+4個數據位。故并行乘法計算例程需要光學處理器的數據位數總量為:
VT=q×VM+r×(5VA+4) (5)
結構量計算機的光學處理器運算位數眾多,但畢竟計算資源是有限的,目前最新應用實驗系統SD11可供分配和使用的數據位數可擴展至16384位,要根據乘法例程的計算要求,再結合結構量計算機的具體配置來設計光學處理器的構造方案;
Ⅱ構造M變換器和MSD三步式加法器:對于一個被乘數為n位、乘數為m位的MSD乘法計算例程,要根據位數信息計算處理器的重構參數VM和VA,并提交給三值光學計算機的監控程序。監控程序根據結構量計算機的計算資源使用情況,確定q、r和VT,并提交相應的重構計算要求。數據位管理模塊負責尋找空閑的數據位區段h~h+VT-1,重構模塊負責配置該數據位區段的計算功能, 構造出多個M變換器和MSD三步式加法器,即構造例程專用的結構量處理器,在一個指令下并行實施乘法算法。
以用戶提交64位的乘法運算為例說明數據位的分配和重構策略,此時VM=64,M變換器占用64q個數據位數,VA=137,加法器占用689r個數據位數,VT=64q+689r,VT≤16384,一種數量足夠、運算規模合適的光學處理器構造方案是取q=8,r=16,VT=11536,重構示意圖如圖5;
串行實現64位乘法計算時,M變換耗用時鐘周期為64個,和數項求和耗用時鐘周期為3×(32+16+...+1)=189個,共計253個;而在該重構方案下,每次可并行執行8組M變換,再借助處理器的不對稱結構,全部M變換耗用的時鐘周期為1+0.5×7=4.5個;和數項求和時,第1次迭代求和分2個批次完成,耗用3×2=6個時鐘周期,第2~6次迭代求和可全并行實施,耗用時鐘周期為3×5=15個,共計25.5個時鐘周期,大約可以縮減串行乘法89.9%的計算耗時;
步驟五、MSD乘法例程的實施:使用三值光學計算機完成乘法運算時,在內部乘法計算例程被激活后,通過協調監控程序的任務調度模塊、數據位管理分配模塊、重構模塊以及底層控制軟件等資源來完成運算,數據流圖如圖6,實施步驟如下,
1.用戶通過輸入界面,輸入操作數,選擇運算規則,點擊“確定”按鈕;
2.三值光學計算機自動生成內部專用的輸送信息和命令的文件(San Zhi Guang,SZG);
3.監控程序的任務調度模塊解析SZG文件,獲取A、B的MSD數據和位數信息n、m,根據公式(3)、(4)確定結構量處理器的構造參數VM和VA;
4.監控程序的數據位管理模塊查詢光學處理器的空閑數據位數,根據公式(5)確定參數q和r,并分配數據位區段h~h+VT-1。
5.重構模塊生成重構命令編碼,任務調度模塊生成操作數編碼,并執行格式化操作,然后由任務調度模塊將數據位序、數據和命令等發送至底層控制軟件;
6.重構器執行底層控制軟件發送的重構命令,構造出乘法例程專用的結構量處理器;
7.實施乘法迭代運算。
7-1.底層控制軟件獲取操作數據,完成迭代變量的定義、初始化等操作;
7-2.M變換的數據準備。底層控制軟件復制A和B的每一位,將(an…ai…a1)送入編碼器生成M變換器的控制光路編碼信息,將(bj…bj…bj)(j=1,...,m)送入編碼器生成M變換器的主光路編碼信息;
7-3.實施M變換。將數據編碼信息同時送入q組M變換器運算,解碼器獲取變換結果,重復操作該步驟直到m組M變換全部完成,得到所有的部分積Sj。
7-4.解碼器對Sj(j=1,2,...,m)高位附加m-j個零,末位附加j-1個零,得到Pj;
7-5.和數項迭代求和。
7-5-1.初始化。計算和數項二叉迭代求和的迭代次數,記入變量times,k賦值1;
7-5-2.執行判斷語句若不滿足,則需要增加一個值為0的和數項;
7-5-3.將全部和數項送至編碼器,奇數項和數項P2j-1生成加法器的主光路編碼信息,偶數項和數項P2j生成加法器的控制光路編碼信息,
7-5-4.將相鄰和數項P2j-1和P2j作為一組,同時送入r組加法器運算,解碼器獲取運算結果,并記入Pj,重復操作該步驟直到組加法運算全部完成。
7-5-5.k增加1,解碼器將上一輪迭代得到的部分和作回饋處理,重復步驟7-5-2~7-5-4直到k=times,最終結果記入變量C;
8.運算結果送交用戶,任務調度模塊將乘積C寫入SZG結果文件,經過文件解析后數據轉化為十進制,返回給用戶,本次運算完成。
本發明的有益效果為:1、借助三值光學計算機的應用特征研究了乘法計算例程的并行優化算法,設計了結構量處理器的構造方案,詳細描述了實施步驟,并通過模擬實驗對例程進行了嚴格的驗證。
2、該研究豐富了三值光學計算機的關鍵軟件模塊,提高了三值光學計算機高性能計算的能力,加速推進了三值光學計算機應用進程的發展。
附圖說明:
圖1為本發明的表示數據的示意圖。
圖2為本發明的并行實施M變換的流程圖。
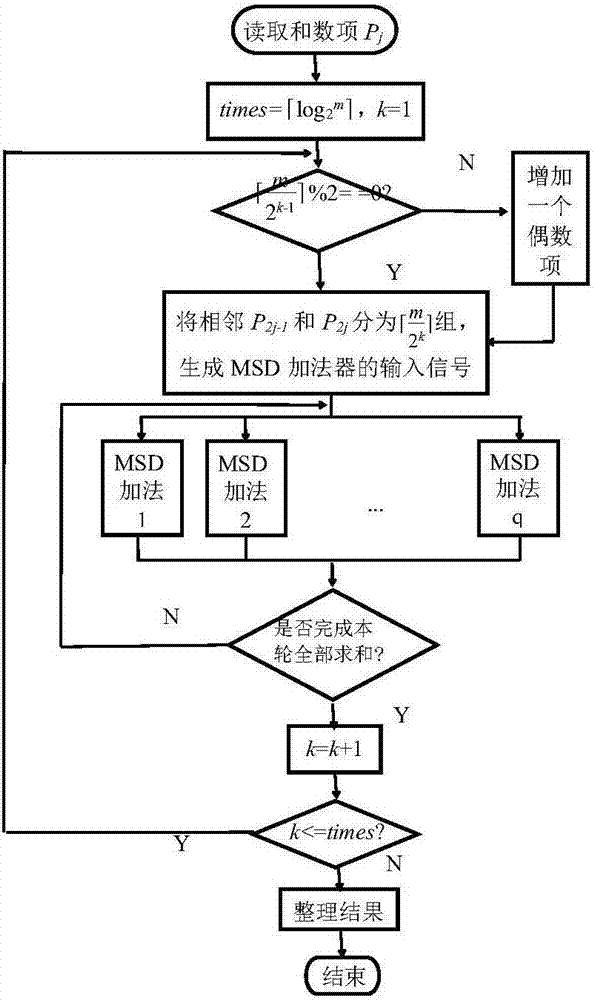
圖3為本發明的并行實施和數項求和的流程圖。
圖4為本發明的步驟三的示意圖。
圖5為本發明的步驟四的重構示意圖。
圖6為本發明的步驟五的數據流圖。
具體實施方式:
為了使本發明實現的技術手段、創作特征、達成目的與功效易于明白了解,下面結合具體圖示,進一步闡述本發明。
如圖1-6所示,結構量計算機的MSD乘法計算的方法,其特征在于:包括以下步驟,
步驟一、表示數據:三值光學計算機采用改良符號數字系統(Modified Signed Digit,MSD)表示數據,即:n位的MSD數字A(an…ai…a1)和m位的B(bm…bj…b1)相乘,ai,bj∈{ī,0,1},運算關系表示為:
計算步驟為,
第1步:計算部分積Sj。將A與B的每一位形成的n位數據(bj…bj…bj)(j=1,2,...,m),送至M變換器上,實施M變換,得到Sj;
第2步:計算和數項Pj。為保證位數的對齊,將Sj高位附加m-j個零,末位附加j-1個零,得到Pj;
第3步:計算∑jPj。將相鄰奇偶和數項兩兩分組,送至三步式MSD加法器依次實施T與W、T'與W'及T2變換(真值表如表1),得到的求和結果又稱為部分和,將作為下一輪加法器的輸入進行回饋運算,直到得到最終結果;
步驟二、并行加速算法:乘法算法是一個循環計算過程,乘法計算例程利用更多的光學處理器數據位數資源,構造出q個M變換器和r個MSD三步式加法器,將內部步驟盡可能作并行處理,用較少運算周期就可以快速獲得計算 結果;
加速策略描述如下:第1步同時并行實施q組M變換,全部M變換運算分個批次完成;第2步可并行對Sj實施補零得到Pj;第3步,第次迭代時,相鄰P2j-1和分配到r個三步式加法器并行實施求和,全部求和分個批次完成;
步驟三、不對稱光路結構改良M變換:三值光學處理器由主光路和控制光路組成,結構上保持著不對稱性;
一次光運算是輸入光信號a和b,得到變換結果c的過程,其運算時間由公式
T=TSY+Tg+TCG+TLC+TC (2)
得到;
三態光發生器SY1和SY2將輸入信號編制成三態光,產生TSY;感光管g轉換三態光為電信號,產生Tg;電信號穿過重構電路CG的反應時間為TCG;CG產生的信號控制液晶LC改變旋光狀態,產生TLC;a依次穿過SY2、偏振片P2、LC、P3生成c,產生TC;在這5個時間里,Tg、TCG以及TLC與控制光路密切相關,并且TLC是最耗時的部分,約為其他部分的幾十倍以上。如果輸入b不變,從第二次運算開始,電信號、重構電路以及液晶狀態都保持不變,TSY+TC后就可以得到變換結果c,可以縮減一半的處理器運算時間;乘法算法計算部分積時,每次都是將A(an…ai…a1)和(bj…bj…bj)送入M變換器,有一路輸入數據A始終保持不變,故可以合理分配數據A至控制光路,以縮短處理器計算延時;
步驟四、構造例程專用的結構量處理器:
Ⅰ按位分配數據位資源:用戶調用乘法例程時,輸入運算請求和原始數據A、B的同時,需要一并給出兩個乘法因子的數字位數n、m,作為分配數據位資源、構造結構量處理器的依據;
計算部分積時,n位的A(an…ai…a1)和(bj…bj…bj)實施M變換生成n位的Sj,需要M變換器的規模為:
VM=n(3)
Sj補零生成n+m-1位的Pj,對Pj進行二叉迭代求和時,每輪迭代輸出結果的 數量會減半,根據三步式MSD加法器的運算規律可知,每輪迭代所需加法器的數據規模增加兩位;
為避免重復構造運算器,以迭代過程中需要加法器的最多位數為準,故加法器的規模為:
三值邏輯變換器的每一位都要占用光學處理器的一個數據位,M變換器共計占用q×VM個數據位,一個VA位的三步式MSD加法器占用5VA+4個數據位。故并行乘法計算例程需要光學處理器的數據位數總量為:
VT=q×VM+r×(5VA+4) (5)
結構量計算機的光學處理器運算位數眾多,但畢竟計算資源是有限的,目前最新應用實驗系統SD11可供分配和使用的數據位數可擴展至16384位,要根據乘法例程的計算要求,再結合結構量計算機的具體配置來設計光學處理器的構造方案;
Ⅱ構造M變換器和MSD三步式加法器:對于一個被乘數為n位、乘數為m位的MSD乘法計算例程,要根據位數信息計算處理器的重構參數VM和VA,并提交給三值光學計算機的監控程序。監控程序根據結構量計算機的計算資源使用情況,確定q、r和VT,并提交相應的重構計算要求。數據位管理模塊負責尋找空閑的數據位區段h~h+VT-1,重構模塊負責配置該數據位區段的計算功能,構造出多個M變換器和MSD三步式加法器[13-14],即構造例程專用的結構量處理器,在一個指令下并行實施乘法算法。
以用戶提交64位的乘法運算為例說明數據位的分配和重構策略,此時VM=64,M變換器占用64q個數據位數,VA=137,加法器占用689r個數據位數,VT=64q+689r,VT≤16384,一種數量足夠、運算規模合適的光學處理器構造方案是取q=8,r=16,VT=11536,重構示意圖如圖6;
串行實現64位乘法計算時,M變換耗用時鐘周期為64個,和數項求和耗用時鐘周期為3×(32+16+...+1)=189個,共計253個;而在該重構方案下,每次可并行執行8組M變換,再借助處理器的不對稱結構,全部M變換耗用的時鐘周期為1+0.5×7=4.5個;和數項求和時,第1次迭代求和分2個批次完成,耗用3×2=6個時鐘周期,第2~6次迭代求和可全并行實施,耗用時鐘周期為3×5=15 個,共計25.5個時鐘周期,大約可以縮減串行乘法89.9%的計算耗時;
步驟五、MSD乘法例程的實施:使用三值光學計算機完成乘法運算時,在內部乘法計算例程被激活后,通過協調監控程序的任務調度模塊、數據位管理分配模塊、重構模塊以及底層控制軟件等資源來完成運算,數據流圖如圖6,實施步驟如下,
1.用戶通過輸入界面,輸入操作數,選擇運算規則,點擊“確定”按鈕;
2.三值光學計算機自動生成內部專用的輸送信息和命令的文件(San Zhi Guang,SZG);
3.監控程序的任務調度模塊解析SZG文件,獲取A、B的MSD數據和位數信息n、m,根據公式(3)、(4)確定結構量處理器的構造參數VM和VA;
4.監控程序的數據位管理模塊查詢光學處理器的空閑數據位數,根據公式(5)確定參數q和r,并分配數據位區段h~h+VT-1。
5.重構模塊生成重構命令編碼,任務調度模塊生成操作數編碼,并執行格式化操作,然后由任務調度模塊將數據位序、數據和命令等發送至底層控制軟件;
6.重構器執行底層控制軟件發送的重構命令,構造出乘法例程專用的結構量處理器;
7.實施乘法迭代運算。
7-1.底層控制軟件獲取操作數據,完成迭代變量的定義、初始化等操作;
7-2.M變換的數據準備。底層控制軟件復制A和B的每一位,將(an…ai…a1)送入編碼器生成M變換器的控制光路編碼信息,將(bj…bj…bj)(j=1,...,m)送入編碼器生成M變換器的主光路編碼信息;
7-3.實施M變換。將數據編碼信息同時送入q組M變換器運算,解碼器獲取變換結果,重復操作該步驟直到m組M變換全部完成,得到所有的部分積Sj。
7-4.解碼器對Sj(j=1,2,...,m)高位附加m-j個零,末位附加j-1個零,得到Pj;
7-5.和數項迭代求和。
7-5-1.初始化。計算和數項二叉迭代求和的迭代次數,記入變量times,k賦值1;
7-5-2.執行判斷語句若不滿足,則需要增加一個值為0的和數項;
7-5-3.將全部和數項送至編碼器,奇數項和數項P2j-1生成加法器的主光路編碼信息,偶數項和數項P2j生成加法器的控制光路編碼信息,
7-5-4.將相鄰和數項P2j-1和P2j作為一組,同時送入r組加法器運算,解碼器獲取運算結果,并記入Pj,重復操作該步驟直到組加法運算全部完成。
7-5-5.k增加1,解碼器將上一輪迭代得到的部分和作回饋處理,重復步驟7-5-2~7-5-4直到k=times,最終結果記入變量C;
8.運算結果送交用戶,任務調度模塊將乘積C寫入SZG結果文件,經過文件解析后數據轉化為十進制,返回給用戶,本次運算完成。
本發明的有益效果為:1、借助三值光學計算機的應用特征研究了乘法計算例程的并行優化算法,設計了結構量處理器的構造方案,詳細描述了實施步驟,并通過模擬實驗對例程進行了嚴格的驗證。
以上顯示和描述了本發明的基本原理和主要特征和本發明的優點。本行業的技術人員應該了解,本發明不受上述實施例的限制,上述實施例和說明書中描述的只是說明本發明的原理,在不脫離本發明精神和范圍的前提下,本發明還會有各種變化和改進,這些變化和改進都落入要求保護的本發明范圍內。本發明要求保護范圍由所附的權利要求書及其等效物界定。
- 還沒有人留言評論。精彩留言會獲得點贊!