基于滑動窗口T?S模糊神經網絡模型的鐵水硅含量預測方法與流程

本發明屬于工業過程監控、建模和仿真領域，特別涉及一種改進型EMD-Elman神經網絡預測鐵水硅含量的方法。
背景技術：
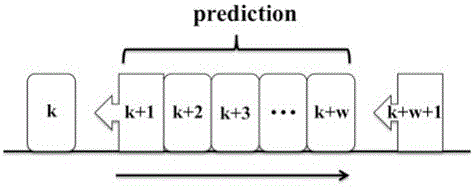
：高爐內復雜的傳質傳熱、多相反應和密閉性，使得高爐具有復雜的時變、動態、非線性、強慣性和多尺度的特性，讓高爐中的煉鐵過程成為最復雜的工業生產過程之一。高爐內的高溫高壓、強腐蝕、強干擾的環境，使得我們很難直接測得爐內的熱狀況。但是，鐵水中硅含量和爐溫呈線性相關，可以反映鐵水的品質，人們通常用鐵水中硅含量的大小來表示爐溫的高低。硅含量過高代表爐溫過高，會消耗額外的燃料，并且會降低鐵的產量；而硅含量低表示爐內溫度較低，可能引發凍缸等事故。因此，為了高爐的穩定順行，人們需要將爐溫控制在一定的合理范圍內，硅含量的預測就顯得尤為重要。高爐內硅的變化主要由以下三個反應構成：1/2CO+O2＝1/2CO2SiO2+CO＝SiO(g)+CO2SiO(g)+C＝Si+CO通過阿倫尼烏斯方程可知，溫度和濃度對化學反應速率有很大的影響，在硅的相關反應中，可以看出溫度、氧氣濃度和一氧化碳濃度對鐵水硅含量的影響最大。因此，有的學者通過動力學和熱力學來建立了鐵水硅含量預測的機理模型，他們關注反應過程中的熱量和質量守恒。但是，因為高爐內復雜的傳質傳熱、相變化和化學反應，使得機理建模很少能夠準確的預測硅的含量。如今，檢測手段的發展使得我們可以測得大量的數據，而電腦技術的迅猛發展使得我們可以在短時間內進行大量的運算，這些技術進步使得基于數據驅動的建模變得更加容易，也成為主流的建模方法。已經存在的基于數據驅動的模型有神經網絡、線性回歸、混沌和支持向量機模型等，它們在某些方面都有自己各自的長處。例如，Jiang提出的混沌粒子群優化算法能夠很好地預測制藥工業中連續反應釜中的溫度。但是，這些模型都是建立在確定的數據集上，不適用于工業在線預測。T-S模糊神經網絡擁有很強的自適應能力，能夠自動更新模型結構參數，并能修正模糊子集的隸屬度函數，可以很好地用來預測控制煉鐵過程中的鐵水硅含量。通過結合滑動窗口模型，模型能夠隨時更新訓練樣本集，進而更新T-S模糊神經網絡的參數和系數。滑動窗口T-S模糊神經網絡能夠很好地適應煉鐵過程的動態、非線性和強慣性的特點，在鐵水硅含量的預測上表現出很好的性能。技術實現要素：針對現有硅含量預測模型的不足之處，提出了一種基于滑動窗口T-S模糊神經網絡的鐵水硅含量預測方法。該方法選用滑動窗口模型和T-S模糊神經網絡模型建模，并選取11個主要參數作為模型的輸入，將硅含量作為模型的輸出。該方法具有較高的命中率和較小的均方誤差，能夠為高爐的操作人員提供準確的預測，幫助他們提前操作高爐，使高爐穩定順行。該方法由以下步驟組成：步驟一：選取T-S模糊神經網絡模型，并組合滑動窗口模型，用于硅含量的預測。步驟二：通過實際經驗和互信息計算選取11個參數作為模型的輸入，硅含量作為輸出。步驟三：將模型初始化后，用歸一化的訓練樣本訓練模型，將訓練好的模型用于硅含量的預測。步驟一所述的T-S模糊神經網絡的結構如下：T-S模糊神經網絡由四層構成，分別是輸入層、模糊化層、模糊規則計算層和輸出層。其中輸入是模糊的，而輸出是確定的，這表示輸出是輸入的線性組合。T-S模糊神經網絡的定義如下：其中是模糊子集，yi是模糊規則的計算輸出。⑴模糊化層是基于概率密度函數μ，其定義如下：式中xj是輸入變量，和是概率密度函數的中心和寬度，k是輸入參數的維度，n是模糊子集的數量。⑵模糊規則計算層由下式構成：⑶輸出層由下式計算得到：步驟一所述的T-S模糊神經網絡的學習算法如下：⑴誤差計算：其中yd是實際值，yc是預測值，e是兩者之差。⑵系數修正：式中是T-S模糊神經網絡的系數，而α是其學習率。⑶參數修正：步驟一所述的滑動窗口模型原理如下：滑動窗口模型是建立在一種假設上，即當前的輸出依賴于當前的輸入，而輸入輸出之間的映射規則可以通過歷史數據得到。根據這個假設，我們預先設定一定量的訓練集樣本，然后不斷地更新樣本數據并舍棄最早的數據點。隨著窗口的滑動，T-S模糊神經網絡會不斷更新其結構參數并給出最新的預測值。步驟二所述的輸入變量的選取過程如下：互信息是檢驗變量相關性的一種重要方法，Kraskov提出了一種k-NN方法可以很方便的用來計算互信息，具體步驟如下所述：式中k是一開始給定的近鄰的個數，ψ是Digamma函數可以表示為：ψ(x)＝Γ(x)-1dΓ(x)/dx它服從以下迭代關系：ψ(x+1)＝ψ(x)+1/xΨ(1)＝-C,C＝0.5772156...為了得到nx和ny，需要計算樣本zi和zj之間的距離di,j：di,j＝||zi-zj||:di,j1≤di,j2≤di,j3...||zi-zj||＝max{||xi-xj||,||yi-yj||}當ε(i)＝max{εx(i),εy(i)}，ε(i)/2被當作zi和k階近鄰的距離。顯然，nx(i)是到xi距離小于ε(i)/2的點的個數，ny(i)是到yi距離小于ε(i)/2的點的個數。通過現場操作工程師的實際經驗建議，我們選取了11個變量作為模型的輸入，它們分別是頂壓、爐頂溫度、透氣性、噴煤、富氧率、全塔壓差、熱風壓力、熱風溫度、熱風流量、空氣濕度和前一爐硅含量。步驟三所述的歸一化方法如下：本發明具有以下優點：1、針對煉鐵過程中高爐的時變、動態、非線性、強慣性和多尺度的特性，選用了具有很強自適應性的T-S模糊神經網絡，它具有很強的學習能力，能夠找出輸入輸出之間的潛在聯系。此外，通過添加滑動窗口，模型能夠很好地跟蹤鐵水硅含量的變化趨勢，提高了預測的精度。2、通過操作經驗和互信息計算，選用了頂壓、爐頂溫度、透氣性、噴煤、富氧率、全塔壓差、熱風壓力、熱風溫度、熱風流量、空氣濕度和前一爐硅含量等對當前硅含量影響最大的11個參數作為模型的輸入變量，能夠充分利用機理建模和數據驅動建模的各自優點。附圖說明圖1是T-S模糊神經網絡的結構示意圖，圖2是滑動窗口的示意圖，圖3是1000爐的鐵水硅含量，圖4是本方法對鐵水硅含量的預測結果。具體實施方式本發明提出了一種基于滑動窗口T-S模糊神經網絡的鐵水硅含量預測方法，該方法由以下步驟組成：步驟一：選取T-S模糊神經網絡模型(如圖1)，并組合滑動窗口模型(如圖2)，用于硅含量的預測。步驟二：通過實際經驗和互信息計算選取11個參數作為模型的輸入，硅含量作為輸出。步驟三：將模型初始化后，用歸一化的訓練樣本訓練模型，將訓練好的模型用于硅含量的預測(如圖4)。步驟一所述的T-S模糊神經網絡的結構如下：T-S模糊神經網絡由四層構成，分別是輸入層、模糊化層、模糊規則計算層和輸出層。其中輸入是模糊的，而輸出是確定的，這表示輸出是輸入的線性組合。T-S模糊神經網絡的定義如下：其中是模糊子集，yi是模糊規則的計算輸出。⑴模糊化層是基于概率密度函數μ，其定義如下：式中xj是輸入變量，和是概率密度函數的中心和寬度，k是輸入參數的維度，n是模糊子集的數量。⑵模糊規則計算層由下式構成：⑶輸出層由下式計算得到：步驟一所述的T-S模糊神經網絡的學習算法如下：⑴誤差計算：其中yd是實際值，yc是預測值，e是兩者之差。⑵系數修正：式中是T-S模糊神經網絡的系數，而α是其學習率。⑶參數修正：步驟一所述的滑動窗口模型原理如下：滑動窗口模型是建立在一種假設上，即當前的輸出依賴于當前的輸入，而輸入輸出之間的映射規則可以通過歷史數據得到。根據這個假設，我們預先設定一定量的訓練集樣本，然后不斷地更新樣本數據并舍棄最早的數據點。隨著窗口的滑動，T-S模糊神經網絡會不斷更新其結構參數并給出最新的預測值。步驟二所述的輸入變量的選取過程如下：互信息是檢驗變量相關性的一種重要方法，Kraskov提出了一種k-NN方法可以很方便的用來計算互信息，具體步驟如下所述：式中k是一開始給定的近鄰的個數，ψ是Digamma函數可以表示為：ψ(x)＝Γ(x)-1dΓ(x)/dx它服從以下迭代關系：ψ(x+1)＝ψ(x)+1/xΨ(1)＝-C,C＝0.5772156...為了得到nx和ny，需要計算樣本zi和zj之間的距離di,j：di,j＝||zi-zj||:di,j1≤di,j2≤di,j3...||zi-zj||＝max{||xi-xj||,||yi-yj||}當ε(i)＝max{εx(i),εy(i)}，ε(i)/2被當作zi和k階近鄰的距離。顯然，nx(i)是到xi距離小于ε(i)/2的點的個數，ny(i)是到yi距離小于ε(i)/2的點的個數。步驟三所述的歸一化方法如下：實施例在鋼鐵生產過程，高爐煉鐵都是極其重要好的環節，其消耗的能耗占整個流程的70％，因此高爐的穩定順行是整個生產過程安全高效運行的保障。因為高爐內的環境極其惡劣，高溫高壓強腐蝕，使得常規的測量手段很難實施，操作人員很難知曉高爐內的實際熱狀況，出鐵時，鐵水損失大量熱量也不能反應實際爐溫。人們通常利用鐵水硅含量來反應爐內的實際狀況，因而鐵水硅含量的預測就顯得極其重要，準確的預測不僅能幫助操作人員合理的調節操作參數，還能指導高爐穩定順行。我們通過研究柳鋼2號高爐的1000組數據(圖3所示)，驗證提出的模型的準確性。下面，我們結合具體過程對實施步驟進行詳細的闡述：步驟一：選取T-S模糊神經網絡模型，并組合滑動窗口模型，用于硅含量的預測。步驟二：通過實際經驗和互信息計算選取11個參數作為模型的輸入，硅含量作為輸出。步驟三：將模型初始化后，用歸一化的訓練樣本訓練模型，將訓練好的模型用于硅含量的預測。通過現場操作工程師的實際經驗建議，我們選取了11個變量作為模型的輸入，它們分別是頂壓、爐頂溫度、透氣性、噴煤、富氧率、全塔壓差、熱風壓力、熱風溫度、熱風流量、空氣濕度和前一爐硅含量。計算它們與當前硅含量的互信息值，得到如下結果：編號變量單位互信息1頂壓kPa0.122爐頂溫度℃0.223透氣性m3/min·kPa0.144噴煤t/h0.295富氧率vol％0.216全塔壓差kPa0.107熱風壓力kPa0.158熱風溫度℃0.329熱風流量m3/min0.1310空氣濕度vol％0.0811前一爐硅含量wt％0.45互信息值介于0到1，越大表示兩個變量相關性越強。從表中可以看出前一爐硅含量與當期硅含量聯系最大，但其余的變量的影響也不能忽略。步驟三所述的歸一化方法如下：我們設定訓練數據的樣本量為400，測試數據集為50。用預測命中率J和均方誤差MSE兩個指標來驗證模型預測的精度：在實際生產過程中，預測誤差小于0.1即可滿足要求。我們提出的模型的命中率達到90％，均方誤差為0.0023。具有很高的精度，完全能滿足實際生產的需求。上述實施例用來解釋說明本發明，而不是對本發明進行限制，在本發明的精神和權利要求的保護范圍內，對本發明做出的任何修改和改變，都屬于本發明的保護范圍。當前第1頁1 2 3