基于遺傳算法的長距離調水工程輸水渠道糙率辨識方法與流程
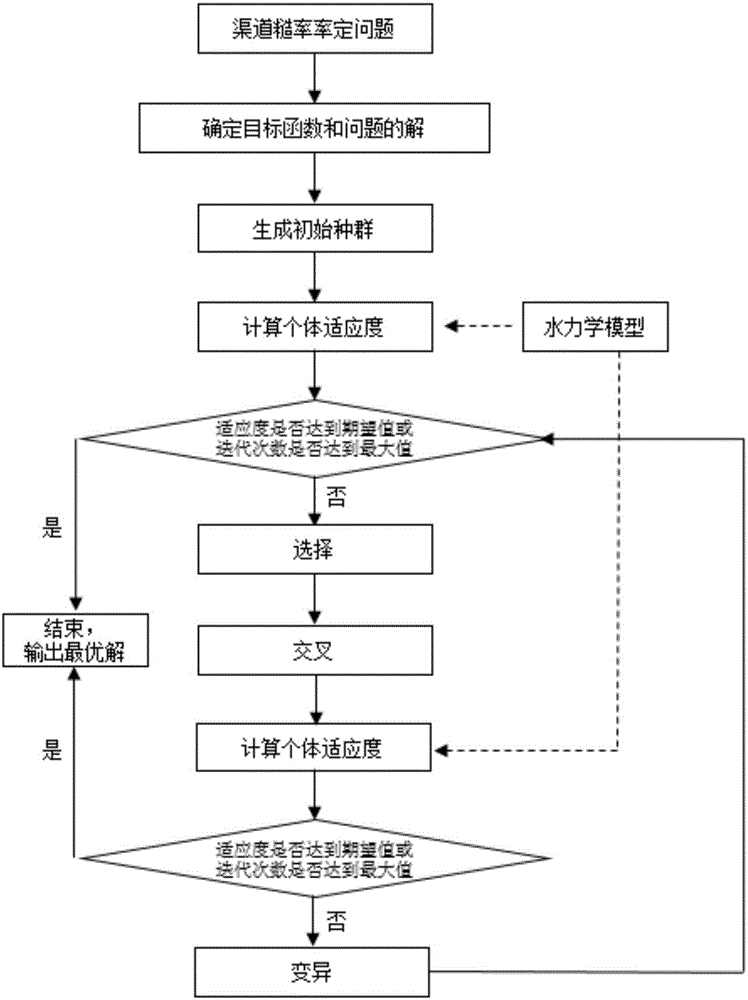
本發明涉及水工設計參數測定領域,尤其涉及一種基于遺傳算法的長距離調水工程輸水渠道糙率辨識方法。
背景技術:
由于水資源存在時空分布不均的問題,難以滿足某些區域社會經濟發展用水需求,建立調水工程是解決這一問題的重要手段,而調水工程多為長距離調水工程,一般含輸水渠道、閘門和分水口等建筑物,由多個渠池串聯從而實現輸水功能。
糙率是渠道表面的粗糙程度和邊壁形狀不規則的綜合表征,也是表達水流經過渠道所受阻力的綜合系數,反映了渠道工程的設計、施工、管理水平,是調水工程設計、運行的關鍵技術參數之一。糙率是決定渠道過水能力的重要參數,對于長距離輸水渠道,其取值的合理可靠性對工程有極其重要的意義。
目前,水利工程多采用曼寧系數表示糙率,一般認為一個斷面或一個渠段擁有相同的糙率值。業界有一種理解:認為糙率是一個物理概念并不是明確的參數,因為在糙率的獲取過程中包含各種不可知因素,所以采取非線性的優選方法,逐步調整糙率的取值,使計算得到的糙率結果更接近測量值,最終確定糙率值。但是,這種方法效率低下,不符合科學技術發展與工程運行管理的需求。
技術實現要素:
本發明的目的在于提供一種基于遺傳算法的長距離調水工程輸水渠道糙率辨識方法,從而解決現有技術中存在的前述問題。
為了實現上述目的,本發明所述基于遺傳算法的長距離調水工程輸水渠道糙率辨識方法,所述方法包括:
S1,確定目標函數和問題的解
在糙率值為nmin≤n≤nmax的范圍內,任意一個單渠段多組工況下的上節制閘閘后水位的模擬值和實測值的相對誤差之和為最小值時,即公式(1),則多組工況下的糙率值為該單渠段的最優值;
設定任意一個單渠段的多組工況下的上節制閘閘后水位的模擬值和實測值的相對誤差之和的最小值為目標函數,設定目標函數所對應的糙率值作為問題的解;
其中,N為工況數量;Oi和Si分別為上節制閘閘后水位在第i個工況的實測值和模擬值;nmin和nmax分別為糙率可取的最小值和最大值;
S2,進行初始化,得初始種群,所述初始種群由多個隨機生成的糙率值組成;
S3,采用一維水力學仿真模型計算初始種群中每個糙率值對應的多組工況下的上節制閘閘后水位,然后計算適應度;
S4,進行終止條件判別,如果符合終止條件,則該糙率值為最優解;如果不符合終止條件,則進入S5;
S5,對初始種群依次進行選擇運算、交叉運算后,
再采用一維水力學仿真模型計算交叉運算后種群中每個糙率值對應的多組工況下的上節制閘閘后水位,然后計算適應度,接著進行終止條件判別,如果符合終止條件,則糙率值為最優解;如果不符合終止條件,則對交叉后的種群進行變異運算,然后返回S3,直至得到糙率值的最優解為止。
優選地,步驟S1中,所述糙率值取值范圍為0.01~0.04。
優選地,步驟S1中,在已知單渠段上節制閘的流量、渠段中分退水口門的流量和下節制閘的閘前水深的前提下,使用非恒定流計算水位變化過程或恒定流模型推求水面線,確定單渠段上節制閘的閘后水位。
優選地,步驟S2中初始化種群,具體按照下述步驟實現:隨機生成M個糙率值組成初始種群P(0);其中,每條染色體的基因位個數可設為9,十進制數值范圍為0-511,除以10000后即可為糙率取值范圍。
優選地,步驟S3和步驟S5中,適應度的計算均采用公式(2):
M為初始種群中糙率的個數,nm表示第m個糙率。
優選地,所述終止條件為適應度為期望值和/或所得糙率值的迭代次數為最大值。
本發明的有益效果是:
本發明所述長距離調水工程輸水渠道糙率辨識方法克服現有技術的不足,本發明所述方法在長距離調水工程中,建立能夠適應工程特征的一維水力學仿真模型,可模擬渠道在各種工況下的水力變化過程;然后基于工程實測數據,將水力學模型與遺傳算法相結合,辨識出各渠池糙率的最優值。
附圖說明
圖1是遺傳算法辨識渠道糙率方法流程示意圖;
圖2是長距離調水工程示意圖;
圖3是單渠池運行示意圖;
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖,對本發明進行進一步詳細說明。應當理解,此處所描述的具體實施方式僅僅用以解釋本發明,并不用于限定本發明。
實施例
本實施例所述基于遺傳算法的長距離調水工程輸水渠道糙率辨識方法,所述方法包括:
S1,確定目標函數和問題的解
在糙率值為nmin≤n≤nmax的范圍內,任意一個單渠段多組工況下的上節制閘閘后水位的模擬值和實測值的相對誤差之和為最小值時,即公式(1),則多組工況下的糙率值為該單渠段的最優值;所述糙率值取值范圍為0.01-0.04;
設定任意一個單渠段的上節制閘閘后水位的多組工況下的模擬值和實測值的相對誤差之和的最小值為目標函數,設定目標函數所對應工況下的糙率值作為問題的解;
其中,N為工況數量;Oi和Si分別為上節制閘閘后水位在第i個工況的實測值和模擬值;nmin和nmax分別為糙率可取的最小值和最大值;
S2,進行初始化,得初始種群,所述初始種群由多個隨機生成的糙率值組成;
S3,采用一維水力學仿真模型計算初始種群中每個糙率值對應的多組工況下的上節制閘閘后水位,然后計算適應度;
S4,進行終止條件判別,如果符合終止條件,則該糙率值為最優解;如果不符合終止條件,則進入S5;
S5,對初始種群依次進行選擇運算、交叉運算后,
再采用一維水力學仿真模型計算交叉運算后種群中每個糙率值對應的多組工況下的上節制閘閘后水位,然后計算適應度,接著進行終止條件判別,如果符合終止條件,則糙率值為最優解;如果不符合終止條件,則對交叉后的種群進行變異運算,然后返回S3,直至得到糙率值的最優解為止。
更詳細的解釋說明為:
(一)在已知單渠段上節制閘的流量、渠段中分退水口門的流量和下節制閘的閘前水深的前提下,使用非恒定流計算水位變化過程或恒定流模型推求水面線,確定單渠段上節制閘的閘后水位。
1、非恒定流計算水位變化過程
本申請針對長距離調水工程特點,采用一維水力學模型,對閘門、明渠等復雜的內部構筑物進行概化處理,將概化好的內部建筑物與圣維南方程組進行耦合,同時采用Preissmann四點時空偏心格式對方程組進行離散,用雙掃描法求解得到糙率的最優解。
非恒定流計算采用一維圣維南方程組,該方程由連續性方程和動量方程組成:
式中(2):x和t分別為空間和時間坐標;q為單位長度渠道上的側向入流流量;α為動量修正系數;Q為斷面流量;A為斷面過水面積;Z為水位;Sf為水力坡度。
式(3)中:K為流量模數。
2、恒定流模型推求水面線
恒定流計算模型應能計算明渠的恒定非均勻流水面線,即明渠穩定輸水時的水流狀態。令式(1)中的時間項和為0,則得到恒定流計算式:
對于式(4)用式(2)的離散格式和數值計算方法進行求解,可使非恒定流收斂到相應的恒定流上,即恒定流計算與非恒定流計算滿足“相容性”準則。
(二)步驟S2中初始化種群,具體按照下述步驟實現:隨機生成M個糙率值組成初始種群P(0);其中,每條染色體的基因位個數可設為9,十進制數值范圍為0-511,除以10000后即可為糙率取值范圍。
(三)步驟S3和步驟S5中,適應度的計算采用公式(2):
M為初始種群中糙率的個數,nm表示第m個糙率。
(四)關于選擇運算、交叉運算和變異運算
1、選擇運算:
將選擇算子作用于群體。即,根據個體適應度來判斷優選個體,直接遺傳到下一代或通過配對交叉產生新的個體再遺傳到下一代。個體適應度評估方法有冒泡法、輪盤賭法等。
2、交叉運算:
將交叉算子作用于群體。即,隨機產生交叉點,將基因位進行交叉。
3、變異運算:
將變異算子作用于群體。即,隨機產生要變異的染色體號和基因位號,對群體中的個體串的某些基因位上的基因值作變動(0變為1;1變為0)。其中,變異應遵從小概率進行。
(五)所述終止條件為適應度為期望值和/或所得糙率值的迭代次數為最大值。
將本實施例所述方法應用于南水北調中線工程第二個渠池(刁河節制閘-湍河節制閘)的糙率辨識中。刁河節制閘的閘后渠底高程為138.456m,湍河節制閘的閘前渠底高程為137.603m,渠道底寬為19m,邊坡為2。選取7組穩定工況的數據(表1)進行分析。
表1刁河節制閘-湍河節制閘渠段工況表
Tab.1 Working conditions of the channel from Diaohe Gate to Tuanhe Gate
選取的工況為穩定工況,所以應用恒定流模型推求水面線即可。模型的上邊界條件可選為刁河節制閘的流量,下邊界條件可選為湍河節制閘閘前水深。南水北調中線工程渠道的設計糙率為0.015,應用到模型中可得7組工況的相對誤差之和為0.0879%。而應用本發明建立的基于遺傳算法的渠道糙率辨識方法,可優化出當相對誤差總和最小(0.0446%)時,糙率為0.0164.證明應用本方法辨識出的糙率,應用到水力模擬中精度更高。
通過采用本發明公開的上述技術方案,得到了如下有益的效果:本發明所述長距離調水工程輸水渠道糙率辨識方法克服現有技術的不足,本發明所述方法在長距離調水工程中,建立能夠適應工程特征的一維水力學仿真模型,可模擬渠道在各種工況下的水力變化過程;然后基于工程實測數據,將水力學模型與遺傳算法相結合,辨識出各渠池糙率的最優值。
以上所述僅是本發明的優選實施方式,應當指出,對于本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以做出若干改進和潤飾,這些改進和潤飾也應視本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!