一種面向裝配規劃的符號加權約束求解方法與流程

本發明涉及裝配序列規劃技術領域，具體涉及一種面向裝配規劃的符號加權約束求解方法。

背景技術：

裝配序列規劃(Assembly Sequences Planning，ASP)是裝配規劃中的一個技術難點，在產品設計開發和生產過程中占有很重要的地位。對于大規模產品的生產，一條優秀的裝配序列將會大大的縮短產品的生產周期，降低產品的生產費用，提高產品的質量性能。

用于減緩或者部分程度上避免組合復雜性問題的一種可行策略是采用符號或者隱式描述技術。有序二叉決策圖(Ordered Binary Decision Diagrams，OBDD)及其擴展形式可以實現狀態空間或者變量組合的隱式表示和搜索，是迄今為止最為有效的符號技術之一。近年來，OBDD及其擴展形式(比如ADD和ZBDD)在裝配序列規劃方面已經有了一些應用。實驗結果表明，利用OBDD或其擴展形式作為裝配序列的表示比使用AND/OR圖表示占用更小的存儲空間。

約束滿足問題(Constraint Satisfaction Problem，CSP)作為人工智能和計算機科學領域中的大量復雜問題的一個通用的求解范例，已得到廣泛的應用。CSP的求解技術為解決裝配序列規劃問題提供了新的思路和手段。然而，現有的CSP求解技術主要在不考慮裝配代價的模型上進行研究，當CSP中對約束的限制過多時，往往會使得問題無解。

技術實現要素：

本發明所要解決的是現有約束滿足問題求解技術不考慮裝配體的裝配代價的問題，提供一種面向裝配規劃的符號加權約束求解方法，其能夠求解出裝配規劃的最優裝配序列。

為解決上述問題，本發明是通過以下技術方案實現的：

一種面向裝配規劃的符號加權約束求解方法，包括步驟如下：

步驟1.獲得裝配體知識，即裝配聯接圖、移動向量矩陣和所需的裝配代價指標；

步驟2.根據裝配體知識，將一個裝配序列規劃問題描述成一個加權約束滿足問題；

步驟3.根據裝配體的裝配聯接圖，創建裝配聯接圖的OBDD表示；

步驟4.根據裝配體的移動向量矩陣，創建移動向量矩陣的OBDD表示；

步驟5.根據所需的裝配代價指標，創建裝配代價指標矩陣的ADD表示；

步驟6.將裝配聯接圖的OBDD表示、移動向量矩陣的OBDD表示和裝配代價指標矩陣的ADD表示代入到步驟2的加權約束滿足問題中，并通過求解加權約束滿足問題去搜索出一條最優的可行的裝配。

上述步驟2的具體步驟如下：

步驟21.用加權約束滿足問題中的變量來表示具有連接關系的兩零件在建立裝配關系時在裝配序列中的順序號，即裝配聯接圖中的一條連接邊對應加權約束滿足問題中的一個變量，并生成變量集X＝{v₁，v₂，v₃，...，v_m}；

步驟22.根據裝配體的零件個數n，設定加權約束滿足問題中各變量的域D為[1，n-1]；

步驟23.對加權約束滿足問題進行約束定義；

步驟24.根據約束定義設置加權約束滿足問題的賦值結構。

上述步驟23中所定義的約束為：

約束1.加權約束滿足問題中的每一個變量只能取各自域中的值，且對于域中的任意一個值d_i∈[1，n-1]，在加權約束滿足問題中至少存在一個變量取值為d_i；

約束2.連接邊e_i1，e_i2，...e_ik在裝配聯接圖中構成了回路，則當有k-1條連接邊建立后，那么第k條連接邊也自然建立，且與前k-1條連接邊中的最后一條建立的連接邊同時建立，同時建立的兩條連接邊對應的變量取值相同；

約束3.當前建立的連接邊所關聯的零件或子裝配與已裝配的子裝配之間必須滿足幾何可行性約束，且計算約束代價。

上述步驟6的具體步驟如下：

步驟61.創建一個OPEN表用于存放聯接零件的每一條聯接邊，創建一個CLOSED表用于存放將要擴展的聯接邊，創建一個EXPEND表用于存放生成的子裝配體SA_new；

步驟62.對裝配代價指標矩陣的ADD表示進行ADD運算，依次計算出裝配聯接圖每條聯接邊聯接的兩零件裝配時所需的代價值，記做單步代價值C_i，i∈[1，n-1]；

步驟63.初始化OPEN表，將裝配聯接圖的每條聯接邊e_i存放入OPEN表中，記錄count＝0；

步驟64.選擇OPEN表中單步代價值最小的聯接邊e_j放入到CLOSED表中，并將其從OPEN表中刪除，擴展e_j下一步所有可能的聯接邊e_k，記錄為<e_i，e_j>，計算所有可能聯接邊的單步代價值C_k；即

步驟641.應用排序算法，對OPEN表中聯接邊的代價值大小排序，選擇出代價值最小的聯接邊e_i；

步驟642.將選出的e_i放入CLOSED表中，將e_i聯接的零件構成一個子裝配體SA_new，放入EXPEND表中，并將e_i從OPEN表中刪除；

步驟643.對e_i進行擴展，選擇另外一條聯接邊e_j，j∈[1，n-1]，j≠i，判斷EXPEND表中的子裝配體SA_new與聯接邊e_j關聯的零件的幾何可行性；

若幾何可行，則計算相應的代價值C_k，并更新EXPEND表；

若幾何不可行，則繼續擴展e_i可能的聯接邊；

步驟644：將擴展的聯接邊<e_i，e_j>插入到OPEN表中，重新對OPEN表中聯接邊的代價值大小排序；

步驟65.將已賦值的變量放入集合assigned中，對所有未賦值的變量逐一考查，判斷該變量所對應的連接邊是否與assigned中的變量所對應的連接邊構成回路，若是，則置該變量值為相應回路中已賦值變量的最大值，并將該變量加入到assigned中，直到assigned不再改變；

步驟66.若count＝n-1，則找到一個可行裝配序列，計算此可行裝配序列的總代價值C_m；

步驟67.對其余未擴展結束的聯接邊e_k依次進行擴展；每擴展一次，先計算當前總的代價值C_n，再比較C_m和C_n；

若C_m<C_n，則停止對此邊擴展，重新選取邊進行擴展判定；

若C_m>C_n，則繼續對此邊進行擴展，且每擴展一次進行一次擴展判定；

步驟68.若找到一個可行裝配序列，且它的代價值C_n<C_m，則替代上一個可行裝配序列，更新代價值C_m，C_m＝C_n，轉67；

步驟69.對所有聯接邊判定完之后，最終得到的可行裝配序列，即為最優裝配序列。

上述步驟643的具體步驟如下：

步驟6431.對e_i進行擴展，選擇一條聯接邊e_j，j∈[1，n-1]，j≠i，判斷選擇的聯接邊是否被擴展；若沒有，則進行擴展；若有，則重新選擇；

步驟6432.根據e_j關聯的兩個零件P₁和P₂的情況進行處理；

Ⅰ.若P₁和P₂分別屬于EXPEND中兩個對立的子裝配體SA_j和SA_k，則SA_j和SA_k構成一個新的子裝配體SA_new，并判斷EXPEND表中其余子裝配體與SA_new的幾何可行性；

若幾何可行，計算擴展e_j的代價值C_k，并從EXPEND表中刪除子裝配體SA_j和SA_k，插入新的子裝配體SA_new；

若幾何不可行，則重新選擇擴展邊，轉步驟6431；

Ⅱ.若p1和p2中只有一個在EXPEND中的子裝配體中，其中P1為SA_j中的零件，P2不在任何子裝配體中，則判斷SA_j與P2的幾何可行性；

若幾何不可行，轉6431；

若幾何可行，則生成一個新的子裝配體SA_new，并判斷EXPEND表中其余子裝配體與SA_new的幾何可行性；

若幾何可行，計算擴展e_j的代價值C_k，并從EXPEND表中刪除子裝配體SA_j并插入子裝配體SA_new；

若幾何不可行，則重新選擇擴展邊，轉6431；

Ⅲ.若P₁和P₂都不在EXPEND表的子裝配體中，則判斷EXPEND中的各子裝配體與{P1，P2}的幾何可行性；

若SA_j與{P1，P2}為幾何不可行，則轉步驟6431；

若都為幾何可行，計算擴展e_j的代價值C_k，則P₁和P₂構成一個新的子裝配體，插入EXPEND表中。

與現有技術相比，本發明用于在已知裝配知識的前提下生成最優裝配序列，其能夠在較高的時間和空間效率下，通過分析所有可能的裝配操作保證裝配序列的完備性，通過判斷局部裝配幾何可行性保證裝配序列的可靠性，通過運用求解加權約束問題的相關技術保證算法的高效性，最終完成對裝配體的最優裝配序列的生成。

附圖說明

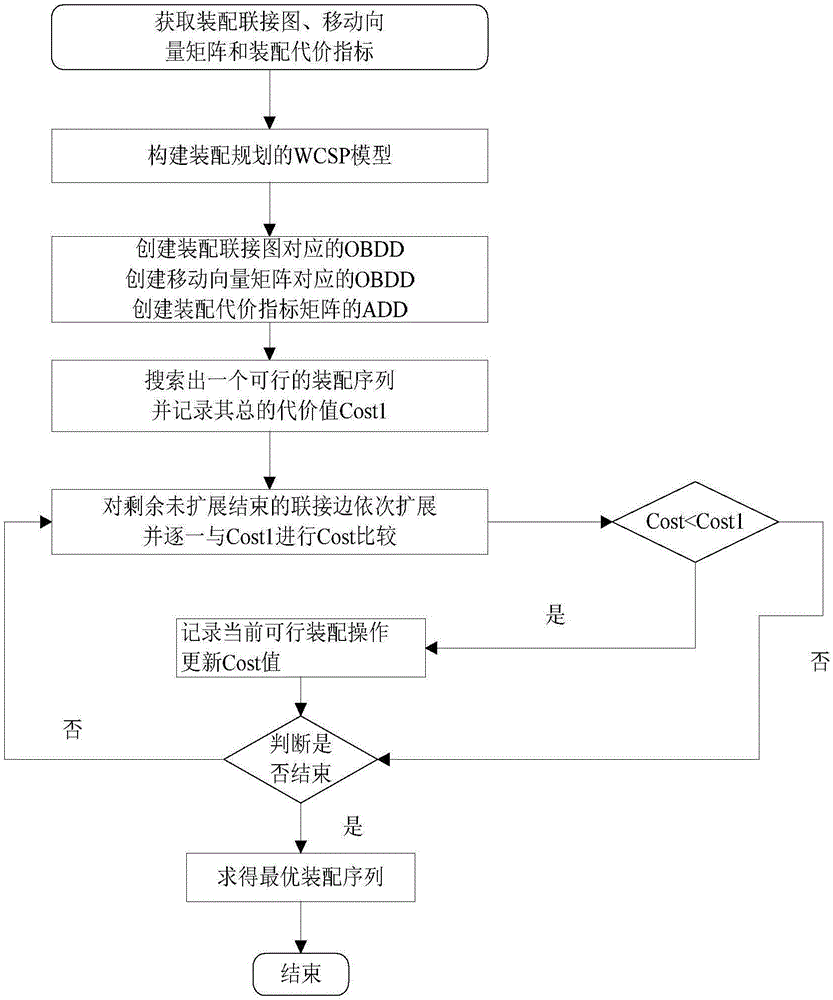
圖1一種面向裝配規劃的符號加權約束求解方法的流程圖。

圖2是本發明的一個實施例的模型圖。

圖3是圖2所示實施例的聯接圖。

圖4是圖2所示實施例的移動向量矩陣。

圖5是圖2所示實施例的裝配代價指標矩陣。

圖6是圖2所示實施例的聯接圖的OBDD表示圖。

圖7是圖2所示實施例的移動向量矩陣的OBDD表示圖。

圖8是圖2所示實施例的裝配代價指標矩陣的ADD表示圖。

圖9是圖2所示實施例的最優裝配序列的ADD表示圖。

具體實施方式

為了使本發明的技術方案及優點更加清楚明白，以下結合附圖及實施例，對本發明的一種面向裝配規劃的符號加權約束求解方法進行進一步的詳細說明。應當理解，此處所描述的具體實施例僅僅用以解釋本發明，并不用于限定本發明。

針對CSP中對約束的限制過多時，往往會使得問題無解的情況，本發明引入加權約束滿足問題(Weighted CSP，WCSP)這一典型的軟約束結構，其基本思想是在CSP的基礎上對每個約束值對賦于一個約束權值，該約束權值用來表示該約束在相應賦值下所產生的約束代價，因此WCSP的求解目標就是求解變量集的完全賦值使其涉及約束的約束代價之和最小。與經典約束滿足問題相比，加權約束滿足問題更具有普遍性且更有廣泛的應用前景。

為此，本發明設計了一種面向裝配規劃的符號加權約束求解方法，首先獲取裝配體的裝配聯接圖、移動向量矩陣和裝配代價指標；然后根據裝配體信息刻劃WCSP模型；接著根據裝配體的裝配聯接圖、移動向量矩陣和裝配代價指標創建聯接圖和移動向量矩陣的OBDD表示以及裝配代價指標的ADD表示；最后搜索出一個可行的裝配序列并記錄其總的代價Cost，再對剩余未擴展完成的聯接邊逐一擴展，并將擴展的代價Cost1與Cost進行比較；搜索完所有的聯接邊之后，最終得到的最小代價值的裝配序列就是最優裝配序列。其能夠在較高的時間和空間效率下，通過分析所有可能的裝配操作保證裝配序列的完備性，通過判斷局部裝配幾何可行性保證裝配序列的可靠性，通過運用求解加權約束問題的相關技術保證算法的高效性，最終完成對裝配體的最優裝配序列的生成。

具體來說，一種面向裝配規劃的符號加權約束求解方法。包括六個步驟，如圖1所示，具體包括六大步驟，即：

步驟1.獲得裝配體知識，給出裝配聯接圖，移動向量矩陣和裝配代價指標矩陣。圖2為一個裝配體模型圖。

步驟2.根據裝配體知識，將一個裝配序列規劃問題描述成一個加權約束滿足問題。包括步驟：

步驟S21.用WCSP中的變量來表示具有連接關系的兩零件在建立裝配關系時在裝配序列中的順序號，即裝配聯接圖中的一條連接邊對應WCSP中的一個變量，設變量集X＝{v₁，v₂，v₃，v₄，v₅}；

步驟S22.裝配體有4個零件，則設WCSP中各變量的域D為[1，3]；

步驟S23.對WCSP進行約束定義；

步驟S231.定義約束1.WCSP中的每一個變量只能取各自域中的值，且對于域中的任意一個值d_i∈[1，3]，在WCSP中至少存在一個變量取值為d_i；

步驟S232.定義約束2.連接邊e_i1，e_i2，...e_ik在裝配聯接圖中構成了回路，則當有k-1條連接邊建立后，那么第k條連接邊也自然建立，且與前k-1條連接邊中的最后一條建立的連接邊同時建立，同時建立的兩條連接邊對應的變量取值相同；

步驟S233.定義約束3.當前建立的連接邊所關聯的零件或子裝配與已裝配的子裝配之間必須滿足幾何可行性約束，且計算滿足約束的代價值。

步驟S24.設置該WCSP問題的賦值結構為S(k)＝([0,1,...,max],+,≥)。[0,1,...,max]為自定義的一個集合，若求解的問題滿足上述定義約束3時，那么單步求解過程中，Cost將被賦值為0,并且將會進一步考慮求解代價值Cost變化；若求解的問題不滿足上述定義約束3時，那么單步求解過程中，Cost將被賦值為max，表示該解不滿足約束定義，將會被刪除。“+”為二元封閉運算，對于a,b[0,1,...,max]，有a+b＝min{max,a+b}。“≥”為自然數集合[0,1,...,max]上的一種全序運算。

步驟3.根據裝配聯接圖，創建聯接圖的OBDD。如圖3是圖2所示裝配體的聯接圖，圖6是圖2所示裝配體的聯接圖的OBDD表示圖。

步驟S31.裝配聯接圖G＝<P，C>。其中G表示裝配體，P為表示裝配體重的各零件的頂點集，對裝配聯接圖的頂點用2位長的二進制串x₀x₁表示，兩個頂點之間的有向邊用x₀x₁y₀y₁表示；

步驟S32.根據建立的所有有向邊，可以得到該裝配聯接圖的布爾特征函數，進而得到裝配聯接圖的OBDD表示，記為OBDD₁。

步驟4.根據裝配體的移動向量矩陣，創建移動向量矩陣的OBDD。如圖4是圖2所示裝配體的移動向量矩陣，圖7是圖2所示裝配體的移動向量矩陣的OBDD表示圖。

步驟S41.對坐標軸的各個方向進行編碼，三維坐標共有+X，+Y，+Z，-X，-Y和-Z六個方向，所以用3位長的二進制串z₀z₁z₂進行編碼；

步驟S42.對于具有4個零件的裝配體，用2位長的二進制串x₀x₁表示裝配體中的零件。對于任意零件對(a，b)，用2位長的二進制串x₀x₁表示零件對的第一個零件，用2位長的二進制串y₀y₁表示零件對的第二個零件，則零件對的二進制串的編碼為x₀x₁y₀y₁；

步驟S43.移動向量矩陣中的第i行(設對應的零件對為(a，b))第j列為1的元素可表示為(x₀x₁)(y₀y₁)·z₀z₁z₂，移動向量矩陣中所有取值為1的元素的特征函數的邏輯“或”運算，得到移動向量矩陣的布爾特征函數；

步驟S44.根據移動向量矩陣的布爾特征函數，運用OBDD的運算和化簡規則，得到移動向量矩陣的OBDD表示，記為OBDD_T。

步驟5.根據裝配體的裝配代價指標矩陣，創建裝配代價指標矩陣的ADD。如圖5是圖2所示裝配體的裝配代價指標矩陣，圖8是圖2所示裝配體的裝配代價指標矩陣的ADD表示圖。

步驟S51.根據裝配代價指標裝配單元的質量U1、聯接關系U2、裝配穩定性U3和裝配序列的重定向次數U4，確定裝配單元的質量代價值Cost₁，聯接類型的代價值Cost₂，裝配體穩定性的代價值Cost₃，重定向次數代價值Cost₄；

步驟S52.根據裝配體零件的裝配方向和裝配零件時所需的代價值，得到一個關于裝配代價指標的矩陣，再運用ADD的運算，得到裝配代價指標矩陣的ADD表示，如圖8所示，記為ADD_C。

步驟6.運用符號OBDD、ADD和求解加權約束滿足問題的相關技術搜索出一條最優的可行的裝配。包括步驟：

步驟S61.創建一個OPEN表用于存放聯接零件的每一條聯接邊，創建一個CLOSED表用于存放將要擴展的聯接邊；創建一個EXPEND表用于存放生成的子裝配體SA_new；

步驟S62.根據裝配代價指標矩陣的ADDc表示，依據ADD相關運算，依次計算出裝配聯接圖每條聯接邊聯接的兩零件裝配時所需的代價值C₁＝7，C₂＝4，C₃＝7，C₄＝7，C₅＝5；

步驟S63.初始化OPEN表，將裝配聯接圖的每條聯接邊e_i存放入OPEN表中，記錄count＝0；

步驟S64.選擇OPEN表中單步代價值最小的聯接邊e_j放入到CLOSED表中，并將其從OPEN表中刪除，擴展e_j下一步所有可能的聯接邊e_k，記錄為<e_i，e_j>，計算所有可能聯接邊的單步代價值C_k；

步驟S641.應用排序算法，對OPEN表中聯接邊的代價值大小排序，選擇出代價值最小的聯接邊e_i(i＝2，C₂＝4)；

步驟S642.將選出的e₂放入CLOSED表中，將e₂聯接的零件構成一個子裝配體SA_new，放入EXPEND表中，并將e₂從OPEN表中刪除；

步驟S643.對e₂進行擴展，選擇另外一條聯接邊e₁，判斷EXPEND表中的子裝配體SA與聯接邊e₁關聯的零件的幾何可行性，幾何可行，則計算相應的代價值C₂₁＝7，并更新EXPEND表；

步驟S644.將擴展的聯接邊<e₁，e₂>插入到OPEN表中，重新對OPEN表中聯接邊的代價值大小排序，跳轉步驟S64。

步驟S65.令assigned＝{已賦值的變量}，對所有未賦值的變量逐一考查，判斷該變量所對應的連接邊是否與assigned中的變量所對應的連接邊構成回路，若是，則置該變量值為相應回路中已賦值變量的最大值，并將該變量加入到assigned中，直到assigned不再改變；

步驟S66.若count＝n-1，則找到一個可行裝配序列，計算此可行裝配序列的總代價值C_m＝18；

步驟S67.對其余未擴展結束的聯接邊e_k依次進行擴展，每擴展一次，先計算當前總的代價值C_n，并比較C_m，C_n，若C_m<C_n，停止對此邊擴展，重新選取邊進行擴展判定；若C_m>C_n，則繼續對此邊進行擴展，且每擴展一次進行一次擴展判定；

步驟S68.若找到一個可行裝配序列，且它的代價值C_n<C_m，則替代上一個可行裝配序列，更新代價值C_m，C_m＝C_n，轉S67；

步驟S69：對所有聯接邊判定完之后，最終得到的可行裝配序列，即為最優裝配序列，算法結束。圖9是圖2所示裝配體的最優裝配序列的ADD表示圖。

為了能夠解決CSP中無法表示裝配體代價指標的問題，本發明應用求解加權約束滿足問題的技術，能夠有效的求解最優裝配序列；此外，本發明利用符號算法的相關技術，降低了裝配序列生成過程中對空間的需求，進而提高裝配序列規劃的效率，擴大求解的規模，并且能夠更好地解決組合爆炸的問題，具有較高的計算效率。

通過結合附圖對本發明具體實施例的描述，本發明的其他方面及特征對本領域的技術人員而言是顯而易見的。

以上對本發明的具體實施例進行了描述和說明，這些實施例應被認為只是示例性的，并不用于對本發明進行限制，本發明應根據所附的權利要求進行解釋。