一種基于有限元結果的連續體表面輕量化方法與流程

本發明涉及一種產品的結構優化方法，更具體地說，涉及一種基于有限元結果的連續體表面輕量化方法，簡化了表面類結構的輕量化生成過程，非常適合增材制造。

背景技術：

增量制造技術的應用始于20世紀80年代，涵蓋產品開發、數據可視化、快速成型和特殊產品制造領域。在90年代增量制造技術在生產領域(分批生產、大量生產和分布式制造)的應用有了進一步發展。21世紀早期增量生產在工業生產的金屬加工領域也第一次達到了前所未有的規模。21世紀初，增量制造相關器械銷量大幅增加，價格大幅下降。咨詢公司Wohlers Associates稱，2012年3D打印機和3D打印服務在全球的價值為22億美元，比2011年增加29％。增量制造技術同時也派生出許多應用服務，涵蓋建筑、工程建造(AEC)、工業設計、汽車、航空、軍事、工程學、口腔和醫藥工業、生物科技(人體器官移植)、時尚、鞋類、珠寶、眼鏡、教務、地理信息系統、飲食等領域。

隨著定制化的3D打印需求不斷增長，需要更有創造性的高性能的輕量化結構材料。各行各業很早便采用拓撲優化技術來構建結構高效的輕量型創新設計。該技術尤其適合與3D打印結合使用，因為拓撲優化能夠制作出自由形態的有機結構，而這樣的結構用傳統制造方法通常很難甚至是無法實現。因而，由于受到特定生產流程的限制，優化設計概念的效率還可能會失效。3D打印提供了前所未有的形態制作自由度，它與拓撲優化技術相結合，在保持結構完整性及性能屬性的同時還使設計表現出更高創造性。

拓撲優化技術運用于明確力學條件的物理模型，可以創造出更為高效的結構模型，但由于生形過程中，參數較多，對邊界條件的選擇相對復雜，拓撲計算過程相對較長，設計師操作技能要求比較高；對于一些力學邊界相對不明確，工況條件復雜的情況往往無法快速進行輕量化生形，不僅提高了建模的成本而且增加了設計時間。

網格化技術現已大量運用于醫療用3D打印材料，多孔性作為對生物醫學植入物的功能性要求，也尤為重要，類似于平板式的結構件仍然缺少成熟的快速生形策略，因此為了實現該類結構輕量化的快速設計制造并保證優良的力學性能，在拓撲優化研究的基礎上，提出一種基于有限元結果的表面輕量化方法，保證結構具有較高結構強度和剛度的前提下，材料消耗大幅度降低，同時擁有美觀的結構化表面。

由于傳統的拓撲優化優化結果較為單一，顯示出典型的力學流線和特征，大部分情況下可以滿足工業及工程要求，但對于類似于醫療護具等受力較小，剛度要求較高，兼有美觀要求的產品，傳統拓撲優化技術難以得到較好的優化成果。

技術實現要素：

1.發明要解決的技術問題

本發明的目的在于提供一種基于有限元結果的連續體表面輕量化方法，采用本發明的技術方案，利用有限元仿真結果，驅動結構網格密度的分布，將曲面類基礎數據分割重構，該方法著重于有限元結果的直觀反饋，通過控制隨機點陣密度與有限元結果相聯系，避免了拓撲優化過程中大規模的迭代試算，加快了結構的生形，簡化了表面類結構的輕量化生成過程，非常適合增材制造。

2.技術方案

為達到上述目的，本發明提供的技術方案為：

本發明的一種基于有限元結果的連續體表面輕量化方法，包含以下步驟：

(1)有限元網格劃分及分域劃分：對連續體表面進行有限元網格劃分，施加邊界條件進行力學有限元計算；根據連續體表面形狀對設計區域進行區塊劃分，建立區塊與有限元網格之間的對應關系；

(2)隨機點布置：根據有限元計算結果的分布，在不同的區塊內設置不同密度的隨機點；

(3)隨機點結構化：根據隨機點的分布，采用結構化算法進行表面結構化，得到平面網格；

(4)實體化：將平面網格進行偏移加厚，形成可打印的實體網格，同時細分已有網格并進行實體光順；

(5)強度驗證：將實體化的連續體重新進行有限元網格劃分，并進行有限元強度分析，若強度無法滿足，則重新從步驟(4)開始，對實體化的連續體進行加厚加粗，最終獲得滿足設計要求的模型。

優選地，在步驟(1)中，區塊可以為均勻大小的區塊，也可以為大小不同的區塊，區塊的大小界定原則為：按區塊內網格計算結果指標方差恒定為依據。

進一步優選地，各區塊的大小界定具體方法為：將連續體表面進行有限元網格劃分，并進行多邊形區塊劃分，區塊內計算單元最大應力為σ_max，應力平均值為E(P)，方差D(P)，各區塊內方差D(P)值應滿足D(P)≤[D(P)]+Δ，Δ為允許偏差值，若某區塊不滿足上式要求，減小該區塊大小后重新布置。

優選地，在步驟(2)中，按以下原則布置隨機點：

(2-1)根據有限元計算結果值干擾均勻隨機點，形成聚向性隨機點陣；

(2-2)隨機均勻點，按照設計區塊內有限元計算結果大小均勻布置對應個數的隨機點。

優選地，在步驟(3)中，采用Delaunay三角網或Voronoi多邊形原則進行表面結構化。

優選地，在步驟(4)中，利用Catmull-Clark算法細分已有網格并進行實體光順。

3.有益效果

采用本發明提供的技術方案，與已有的公知技術相比，具有如下顯著效果：

(1)本發明的一種基于有限元結果的連續體表面輕量化方法，其利用有限元仿真結果，驅動結構網格密度的分布，將曲面類基礎數據分割重構，該方法著重于有限元結果的直觀反饋，通過控制隨機點陣密度與有限元結果相聯系，避免了拓撲優化過程中大規模的迭代試算，加快了結構的生形，簡化了表面類結構的輕量化生成過程，非常適合增材制造；

(2)本發明的一種基于有限元結果的連續體表面輕量化方法，其設計過程簡便易控，輕量化結構結果可根據用戶的喜好進行孔洞疏密定制；

(3)本發明的一種基于有限元結果的連續體表面輕量化方法，其結構在應力較小區塊仍然保留了一部結構件，因此結構對不可預見受力工況具有更高的冗余度；

(4)本發明的一種基于有限元結果的連續體表面輕量化方法，其設計結果能夠兼具堅固性和仿生美觀性。

附圖說明

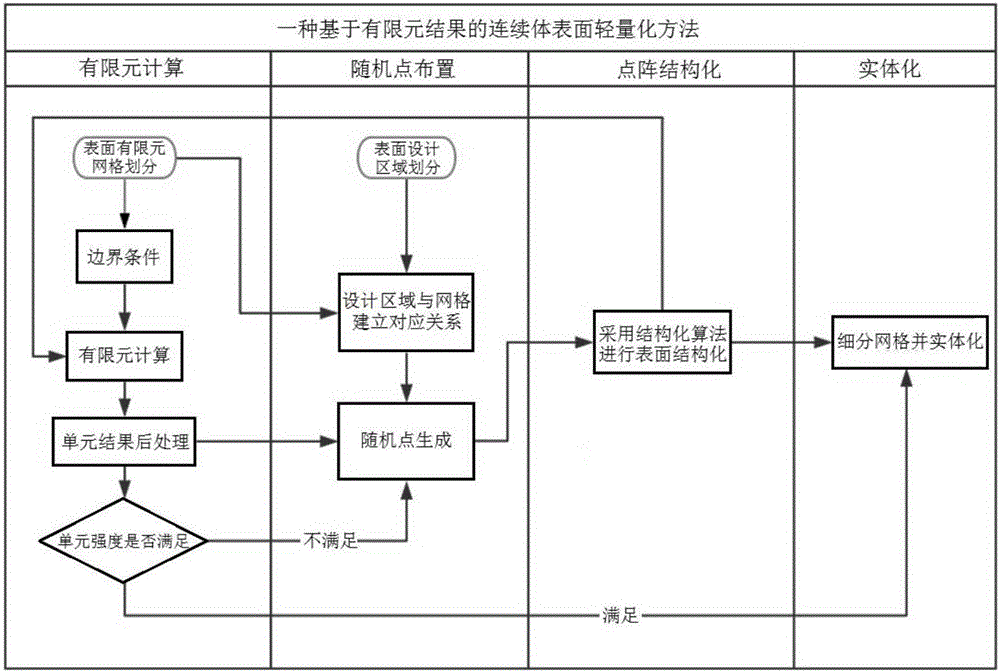
圖1為本發明的一種基于有限元結果的連續體表面輕量化方法的設計流程圖；

圖2為本發明中一種實施例的有限元區塊劃分示意圖；

圖3為本發明中一種實施例的隨機點布置示意圖；

圖4為本發明中一種實施例的隨機點結構化平面網格示意圖；

圖5為本發明中一種實施例的連續體表面輕量化模型示意圖。

具體實施方式

為進一步了解本發明的內容，結合附圖和實施例對本發明作詳細描述。

實施例

結合圖1所示，本實施例的一種基于有限元結果的連續體表面輕量化方法，包含以下步驟：

(1)有限元網格劃分及分域劃分：對連續體表面進行有限元網格劃分，對網格設置材料性質及表面厚度信息，施加邊界條件(荷載邊界條件及約束邊界條件)進行力學有限元計算，獲得單元應變能結果(參見如圖2所示)；根據連續體表面形狀對設計區域進行區塊劃分，建立區塊與有限元網格之間的對應關系；在本實施例中，區塊可以為均勻大小的區塊，也可以為大小不同的區塊，區塊的大小界定原則為：按區塊內網格計算結果指標方差恒定為依據，例如，將連續體表面進行有限元網格劃分，并進行多邊形區塊劃分，區塊內計算單元最大應力為σ_max，應力平均值為E(P)，方差D(P)，各區塊內方差D(P)值應滿足D(P)≤[D(P)]+Δ，Δ為允許偏差值，若某區塊不滿足上式要求，減小該區塊大小后重新布置。

(2)隨機點布置：根據有限元計算結果的分布，在不同的區塊內設置不同密度的隨機點(參見圖3所示)；隨機點的布置可按以下原則：

(2-1)根據有限元計算結果值干擾均勻隨機點，形成聚向性隨機點陣；

(2-2)隨機均勻點，按照設計區塊內有限元計算結果大小均勻布置對應個數的隨機點。

在本實施例中，簡單劃分為四邊形區塊(如圖3所示)，根據網格應變能密度計算區塊均值，各個設計區塊均進行相同的計算，獲得區塊內平均應變能密度根據設定的單區塊基準隨機點數N，進行各區塊隨機點數計算，在i區域布置N_i數量的隨機點。

(3)隨機點結構化：根據隨機點的分布，采用結構化算法進行表面結構化，得到平面網格(參見圖4所示)；具體地，可采用Delaunay三角網或Voronoi多邊形原則進行表面結構化，例如圖4中采用Voronoi多邊形進行表面結構化。

(4)實體化：將平面網格進行偏移加厚，形成可打印的實體網格，同時細分已有網格并進行實體光順，最終獲得實體封閉的網格體(如圖5所示)；具體地，可利用Catmull-Clark算法細分已有網格并進行實體光順。

(5)強度驗證：將實體化的連續體重新進行有限元網格劃分，并導入有限元軟件進行有限元強度分析，若強度無法滿足，則重新從步驟(4)開始，對實體化的連續體進行加厚加粗，最終獲得滿足設計要求的模型，可交付進行3D打印生產。

本發明的一種基于有限元結果的連續體表面輕量化方法，對需求表面進行網格劃分，施加需求邊界條件進行力學計算；根據表面形狀進行設計區域的區塊劃分，建立區塊與有限元計算單元對應關系；根據區塊內的有限元計算結果，統計區塊內單元結果分布，建立大小不同晶格組成的孔狀表面；建立了有限元優化反饋策略，以變密度隨機孔洞規則生成輕量化結構。該方法著重于有限元結果的直觀反饋，通過控制隨機點陣密度與有限元結果相聯系，避免了拓撲優化過程中大規模的迭代試算，加快了結構的生形，簡化了表面類結構的輕量化生成過程，非常適合增材制造；過程簡便易控，輕量化結構結果可根據用戶的喜好進行孔洞疏密定制；同時設計結果能夠兼具堅固性和仿生美觀性。

以上示意性地對本發明及其實施方式進行了描述，該描述沒有限制性，附圖中所示的也只是本發明的實施方式之一，實際的結構并不局限于此。所以，如果本領域的普通技術人員受其啟示，在不脫離本發明創造宗旨的情況下，不經創造性地設計出與該技術方案相似的結構方式及實施例，均應屬于本發明的保護范圍。