一種基于離散廣義Nash匯流模型的河道洪水預報方法與流程
本發明屬于水文預報技術領域,更具體地,涉及一種基于離散廣義Nash匯流模型的河道洪水預報方法。
背景技術:
水文學中現有的河道洪水演算以圣維南方程組為基礎,采用概化分析的方法,將連續方程概化為水量平衡方程,將動力方程概化為槽蓄曲線方程;根據槽蓄曲線的表達形式不同,主要有馬斯京根法、特征河長法和滯后流量演算法。
實際工作中,實際的待演算河段很難滿足這些方法簡化的槽蓄曲線方程;現有技術采取分段連續演算的方法,如馬斯京根匯流曲線、加里寧單位線和Nash瞬時單位線;該類方法實質是分析單位入流形成的出流過程,沒有考慮河槽初始蓄水量的變化情況;而以Nash瞬時單位線理論為基礎的廣義Nash匯流模型,將河槽初始蓄水量的退水過程包含進來,一定程度上提高了預報精度;但廣義Nash匯流公式形式上比較復雜,且包含了積分項,限制了其在工程上的應用。
技術實現要素:
針對現有技術的以上缺陷或改進需求,本發明提供了一種基于離散廣義Nash匯流模型的河道洪水預報方法,其目的在于通過引入滯蓄曲線來簡化廣義Nash匯流模型,并建立離散的廣義Nash匯流模型,以簡化計算,提高預報精度。
為實現上述目的,按照本發明的一個方面,提供了一種基于離散廣義Nash匯流模型的河道洪水預報方法,包括如下步驟:
(1)根據待預報河段的入流量和出流量歷史同步觀測數據選取歷史場次洪水;
(2)建立待預報河段的離散廣義Nash匯流模型;并基于歷史場次洪水信息采用SCE-UA算法對所述離散廣義Nash匯流模型的參數n、K進行優化率定;
其中,n是指Nash線性水庫的個數,K為反映Nash線性水庫調蓄能力的參數;(3)根據當前時刻之前(n-1)△t時段內的出流量與[t,t+△t]時段內的入流量,利用所述離散廣義Nash匯流模型預報(t+△t)時刻的出流量;其中,△t是指計算時段長;
(3)根據當前時刻之前(n-1)△t時段內的出流量與[t,t+△t]時段內的入流量,利用所述離散廣義Nash匯流模型預報(t+△t)時刻的出流量;其中,△t是指計算時段長。
優選地,上述基于離散廣義Nash匯流模型的河道洪水預報方法,其步驟(2)中建立待預報河段的離散廣義Nash匯流模型的方法包括如下子步驟:
(2.1)建立初始條件不為零時的廣義Nash匯流模型:
其中:I(t)、O(t)分別為河段的入流和出流過程,O(j)(0)為O(t)在初始時刻的j階導數,u(·)為Nash瞬時單位線,n是指Nash線性水庫的個數,K為反映Nash線性水庫調蓄能力的參數;
(2.2)采用滯蓄曲線Rn(t)對上述廣義Nash匯流模型進行簡化;
定義滯蓄曲線
其中,為Nash線性水庫個數為n的S-曲線;
將廣義Nash匯流模型進行如下簡化:
則Rn(t)表示Nash線性水庫個數為n時,持續1個單位的入流在河槽中的滯蓄流量,由此,將單位入流一分為二,其中一部分形成出口斷面流量Sn(t),另一部分留在河槽中形成滯蓄流量Rn(t);Rn-j(t)是指t時刻Nash線性水庫個數為(n-j)時的滯蓄流量;
(2.3)對上述簡化的廣義Nash匯流模型進行離散化處理,建立離散廣義Nash匯流模型;
離散廣義Nash匯流模型為:
其中,I(t)是指河段在t時刻的入流量,O(t)是指河段在t時刻的出流量,O(t+△t)是指河段在(t+△t)時刻的出流量,O(t-i△t)是指河段在(t-i△t)時刻的出流量,△I(t+△t)是指[t,t+△t]時段內的入流增量,△I(t+△t)=I(t+△t)-I(t);Rn-j(△t)是指△t時刻線性水庫個數為(n-j)時的滯蓄曲線;Rn(△t)是指△t時刻線性水庫個數為n時的滯蓄曲線,Ri(△t)是指△t時刻,線性水庫個數為i時的滯蓄曲線;j為自然數;滯蓄曲線表示持續1個單位的入流在河槽中的滯蓄流量。
優選地,上述基于離散廣義Nash匯流模型的河道洪水預報方法,其步驟(2.3)包括如下子步驟:
(2.3.1)根據廣義Nash匯流模型的物理含義,以及簡化的Nash匯流模型,建立(t+△t)時刻出流量的預報模型,
即(t+△t)時刻的流量由當前河槽蓄水量的退水與[t,t+△t]時段內上游入流產生的出流組成;
(2.3.2)對上述(t+△t)時刻出流量的預報模型的導數項和積分項進行離散化處理,建立離散廣義Nash匯流模型,
其中:I(t)、O(t)分別為河段在t時刻的入流量和出流量;O(t+△t)是指(t+△t)時刻的出流量;
上述離散廣義Nash匯流模型中,[t,t+△t]時段內上游入流形成的出流量包含兩部分,一部分是當前時刻流量I(t)經過△t形成的出流量,另一部分是該時段內入流增量扣掉滯蓄流量而形成的出流量;即(t+△t)時刻的出流量O(t+△t)是當前時刻之前(n-1)△t時段內的出流量與[t,t+△t]時段內的入流量的線性組合;各項的權重系數通過滯蓄曲線Rn(t)計算得到。
優選的,上述基于離散廣義Nash匯流模型的河道洪水預報方法,其步驟(2.3.2)包括如下子步驟:
(2.3.2.1)對(t+△t)時刻的出流量的預報模型的導數項做離散化處理,具體地,由前向差分近似計算O(t)的各階導數,
其中,為組合數計算公式;
(2.3.2.2)對(t+△t)時刻出流量預報模型的積分項作離散化處理;
(a)假設[t,t+△t]時段內入流I(s)呈線性變化,根據入流I(s)在[t,t+△t]時段內的線性變化情況,將積分項變換為
其中,ΔI(t+Δt)=I(t+Δt)-I(t),是指[t,t+Δt]時段內的入流增量;
由于入流I(s)在[t,t+△t]時段內呈線性變化,對于s∈[t,t+Δt],
(b)令τ=t+Δt-s,根據Sn(t)與u(t)存在的積分關系,利用分部積分公式以及Rn(t)與Sn(t)的關系,將積分項變換為
其中,
優選的,上述基于離散廣義Nash匯流模型的河道洪水預報方法,n取1,2或3。
優選地,上述基于離散廣義Nash匯流模型的河道洪水預報方法,當n=1時,Ot+1=R1Ot+[MK(1-R1)-R1]It+[1-MK(1-R1)]It+1;其中,Ot+1=O(t+Δt),Ot=O(t),It+1=I(t+Δt),It=I(t),R1=R1(Δt),MK=K/Δt。
優選地,上述基于離散廣義Nash匯流模型的河道洪水預報方法,當n=2時,Ot+1=(R1+R2)Ot-R1Ot-1+[MK(2-R1-R2)-R2]It+[1-MK(2-R1-R2)]It+1;其中,Ot+1=O(t+Δt),Ot=O(t),Ot-1=O(t-Δt),It+1=I(t+Δt),It=I(t),R1=R1(Δt),R2=R2(Δt),MK=K/Δt。
優選地,上述基于離散廣義Nash匯流模型的河道洪水預報方法,當n=3時,Ot+1=(0.5R1+R2+R3)Ot-(R1+R2)Ot-1+0.5R1Ot-2
+[MK(3-R1-R2-R3)-R3]It+[1-MK(3-R1-R2-R3)]It+1;
其中,Ot+1=O(t+Δt),Ot=O(t),Ot-1=O(t-Δt),Ot-2=O(t-2Δt),It+1=I(t+Δt),It=I(t),R1=R1(Δt),R2=R2(Δt),R3=R3(Δt),MK=K/Δt。
優選地,上述基于離散廣義Nash匯流模型的河道洪水預報方法,參數n和K根據以下方法確定:
運用枚舉法分別取n=1、2、3,以均方根誤差最小為目標函數,采用可快速搜索到參數全局最優解的SCE-UA算法對參數K進行優化率定,以均方根誤差最小時對應的n和K值作為參數率定結果;
其中,SCE-UA算法是指復合形交叉進化算法,是一種有效的解決非線性約束最優化問題的方法,可以快速地搜索到水文模型參數全局最優解,其基本思路是將基于確定性的復合形搜索技術和自然界中生物競爭進化原理相結合,用來求解最小化問題。
總體而言,通過本發明所構思的以上技術方案與現有技術相比,能夠取得下列有益效果:
(1)本發明提供的基于離散廣義Nash匯流模型的河道洪水預報方法,相比于現有常用的馬斯京根方法,本方法由于充分利用了實測數據的歷史有效信息,可以提高洪峰和洪水過程的預報精度;
(2)本發明提供的基于離散廣義Nash匯流模型的河道洪水預報方法,其所采用的離散廣義Nash匯流模型,相比于現有廣義Nash匯流模型,在形式上表現為若干入流量和出流量的線性組合,更加直觀,便于在實際中推廣應用;
(3)本發明提供的基于離散廣義Nash匯流模型的河道洪水預報方法,相比于其他統計類方法,將線性組合的權重系數表達為滯蓄曲線的函數,參數只有n和K,沒有額外增加參數。
附圖說明
圖1是實施例提供的離散廣義Nash匯流模型的河道洪水預報方法的流程圖;
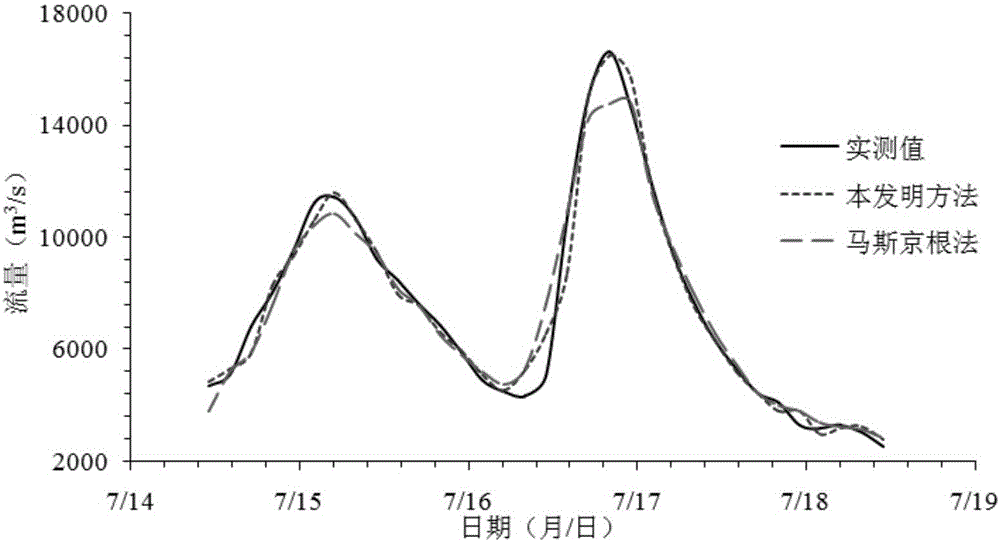
圖2是實施例里的河道洪水預報結果的過程線對比示意圖。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖及實施例,對本發明進行進一步詳細說明。應當理解,此處所描述的具體實施例僅僅用以解釋本發明,并不用于限定本發明。此外,下面所描述的本發明各個實施方式中所涉及到的技術特征只要彼此之間未構成沖突就可以相互組合。
以下通過實施例,具體說明本發明的技術方案。
具體實施例以清江水布埡-隔河巖河段為例進行闡述;水布埡水庫是清江干流中下游河段三級開發的龍頭梯級,隔河巖水庫位于其下游92km處,兩壩址斷面區間流域面積3570km2;兩座水庫除了承擔清江流域的防洪任務外,還為長江洪水錯峰預留了10億m3防洪庫容,以配合三峽水庫減輕長江荊江河段的洪水威脅;水布埡-隔河巖河段高精度的河道洪水預報對清江乃至長江防洪具有重要意義;在本發明中,河段是指上、下控制斷面之間的一段河道。
采用本發明實施例提供的基于離散廣義Nash匯流模型的河道洪水預報方法來進行預報的流程,如圖1所示,具體包括如下步驟:
(1)根據兩水庫壩址斷面處的歷史還原資料,選取該河段1997年7月的一次洪水過程(計算時段△t=3h)進行計算,該場洪水主要由清江中上游暴雨所致,水布埡-隔河巖河段區間來水所占比重較小,為了保持水量平衡,將區間來水按比例均勻分攤到水布埡壩址斷面來水。
(2)建立該河段的離散廣義Nash匯流模型,并以均方根誤差最小為目標函數,采用SCE-UA算法分別離散廣義Nash匯流模型的參數進行優化率定,本發明實施例中,參數n=3,K=1.53h;其中,n是指Nash線性水庫的個數,K為反映Nash線性水庫調蓄能力的參數;
(3)根據當前時刻之前2△t時段內的出流量與[t,t+△t]時段內的入流量,利用該河段的離散廣義Nash匯流模型預報(t+△t)時刻的出流量:
Ot+1=(0.5R1+R2+R3)Ot-(R1+R2)Ot-1+0.5R1Ot-2
+[MK(3-R1-R2-R3)-R3]It+[1-MK(3-R1-R2-R3)]It+1;
其中,Ot+1=O(t+Δt),Ot=O(t),Ot-1=O(t-Δt),Ot-2=O(t-2Δt),It+1=I(t+Δt),It=I(t),R1=R1(Δt),R2=R2(Δt),R3=R3(Δt),MK=K/Δt。
為了驗證本發明所提供的河道洪水預報方法的模擬效果,將本發明所提供的河道洪水預報方法在實施例中的預報結果,與采用馬斯京根法進行預報的效果進行對比;
對兩種方法的精度評價結果如表1所列;
表1洪峰預報精度評價結果
在表1所列舉的數據中,該場洪水共有2個洪峰;馬斯京根法的洪峰相對誤差分別為-5.30%和-10.75%,而采用本實施例提供的方法較馬斯京根法均有較大程度的提高,分別達到1.52%和-0.75%,表現出較強的實時預報能力。
采用馬斯京根法與采用本發明提供的方法對洪水過程的模擬結果對比如圖2所示,通過圖2可以看出,本發明所提供的方法的預報結果與實測過程線更為接近,確定性系數分別達到0.9782,而馬斯京根法的確定性系數只有0.9638;究其原因,本發明所提供的方法除了包含當前時刻出流量Ot之外,還包含了前兩個時刻Ot-1和Ot-2的一些信息,這些信息暗含了洪水過程的變化趨勢,使得本發明所提供的河道洪水預報方法的預報能力表現得更加優異。
本領域的技術人員容易理解,以上所述僅為本發明的較佳實施例而已,并不用以限制本發明,凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等,均應包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!