電磁器件分析中電磁?熱?應力三場耦合的去耦合計算方法與流程

本發明涉及了一種金屬微波器件分析計算方法，尤其是涉及了一種電磁器件分析中電磁-熱-應力三場耦合的去耦合計算方法。

背景技術：

所謂多物理場耦合，指在一個系統中，多個物理場交織在一起，互相影響，互相作用而彼此影響的物理現象，這種現象在客觀世界和工程實際中廣泛存在，只要多個物理場存在且各物理場之間發生了能量交換，必然隨之會產生多物理場耦合系統。各種物理場現象都可以用偏微分方程來描述，如熱、電、力。多物理場的本質是偏微分方程組。

金屬微波器件是非常典型的、具有強烈耦合度的多物理場環境，包括電磁場、溫度場、力場的相互耦合。由于很多因素同時起作用，必須給出一種可以同時處理這些因素作用的多物理場聯合分析方法。

描述金屬微波器件涉及電磁、熱、力多種物理現象的組合，而這些現象都基于特定的物理規律，這些物理規律可借助于偏微分方程得到精確描述和分析。故解決多物理場耦合的基礎是建立它們的數學模型，這需要充分了解各物理場的基本理論，列出其數學模型(偏微分方程組)，多物理場分析意味著求解多維度的偏微分方程組。系統性地討論它們之間的場耦合關系，得到偏微分方程體系，建立電-熱-應力約束條件下的典型空間金屬微波器件模型。

技術實現要素：

為了簡化電磁-熱-應力三場耦合計算的復雜度，本發明的目的在于提供了一種電磁器件分析中電磁-熱-應力三場耦合的去耦合計算方法。

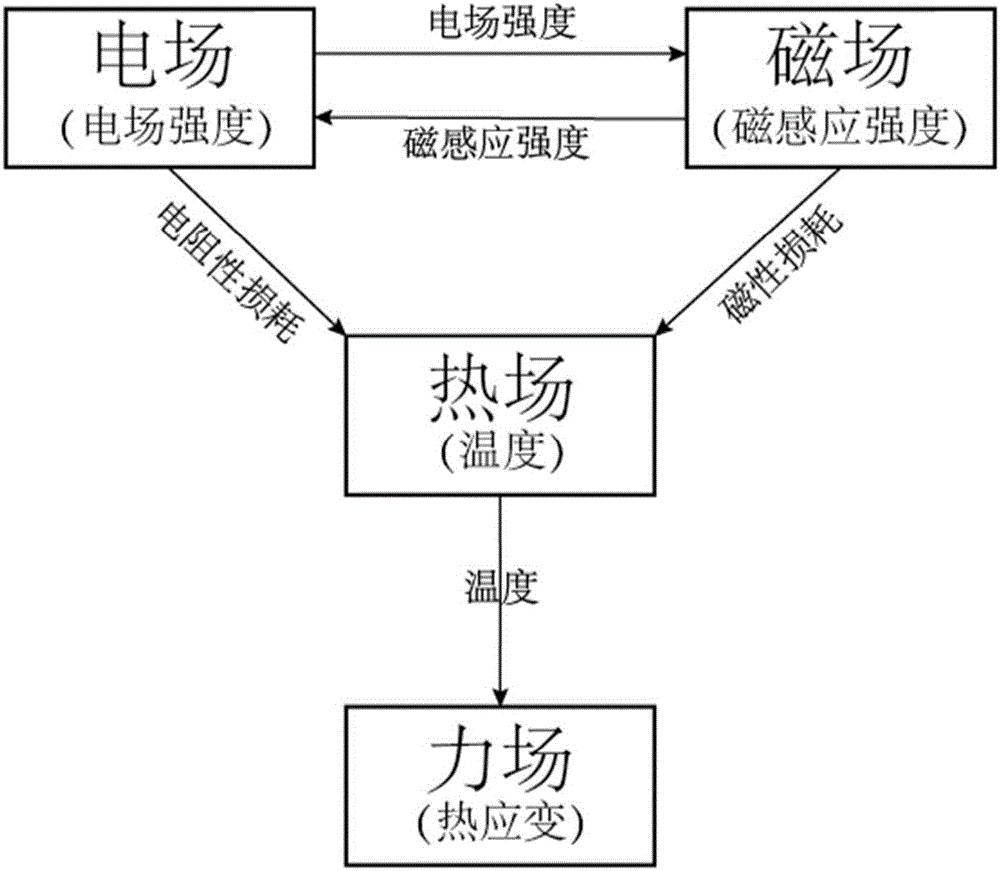
為了達到上述目的，本發明采用的技術方案是如圖1所示：根據電磁波傳播原理與阻抗邊界條件建立電磁波在金屬微波器件內壁的微波電磁損耗模型，通過微波電磁損耗模型將電磁場和力場之間去耦合，使得電磁場通過溫度場間接與力場耦合，進而對力場分布計算。

電磁-熱-力場之間存在著耦合作用，從原理上來說，由于電磁損耗，微波器件中大功率微波的傳播會在微波器件內部產生熱損耗Q(包括電阻性損耗Q_rh與磁性損耗Q_ml)。電阻性損耗可用介質的損耗角正切tanδ或介電常數的虛部ε來表示，與材料的電阻率有關，電阻率越大，阻性損耗越小。磁性損耗主要存在于磁性材料中，與復磁導率的虛部μ成正比。電磁損耗熱效應產生的熱成為溫度場的場源，求解熱傳遞方程可確定溫度場的分布。而溫度場對結構的作用表現為溫度差導致物體的膨脹或縮小，從而產生熱應變ε_inel。作為力場的場源，通過求解線彈性力學方程組可得到應變、位移與應力的分布。現有技術中，電磁場、溫度場和力場三個物理場通過彼此提供物理場場源的方式進行耦合。而本發明使得電磁場和力場之間去耦合，電磁場的電場和磁場與溫度場耦合，溫度場與力場耦合，電場和磁場分別與力場之間不耦合。

所述的平面波入射到金屬微波器件，在金屬微波器件的內部形成電磁場分布并產生熱量，先計算獲得金屬內壁產生的熱損耗分布，熱損耗包括電阻性損耗和磁性損耗，將熱損耗分布作為熱源以賦值到熱應力場的方式進行求解得到溫度場分布，根據溫度場分布計算獲得熱應變分布，獲得去耦合計算結果。

本發明將三個物理場分為兩個步驟電磁-熱、熱-應力進行分步計算，具體是在所述平面波入射到金屬微波器件采用以下方式計算獲得去耦合計算結果：

第一，先通過電場形式下具有附加邊界條件的波動方程獲得金屬微波器件內的電場分布，接著利用麥克斯韋方程組以及金屬微波器件與其外部環境內在的本構關系計算出電位移、磁感應強度、磁場強度和自由電流密度物理量，從而獲得電磁場分布情況；

第二，采用以下公式計算獲得電阻性損耗Q_rh與磁性損耗Q_ml：

其中，Re表示實部，j表示虛數單位，ω表示角頻率，和分別為磁感應強度矢量和磁場強度矢量，為電場強度矢量，為自由電流密度矢量；電阻性損耗可用介質的損耗角正切tanδ或介電常數的虛部ε來表示，與材料的電阻率有關，電阻率越大，阻性損耗越小。磁性損耗主要存在于磁性材料中，與復磁導率的虛部μ成正比。

將電阻性損耗Q_rh與磁性損耗Q_ml相加作為熱源的大小，代入以下熱傳導方程求解獲得問題，進而得到溫度場分布：

其中，ρ為密度，C_ρ為恒壓下的熱容，為傳導熱通量，k為熱導率，Q為熱損耗；

第三，溫度的變化引起熱應變，采用以下公式表示的線彈性力學方程計算得到熱應變ε_inel，進而得到熱應變分布：

ε_inel＝α(T-T_ref)

其中，α為熱膨脹系數，T_ref表示金屬微波器件的原始溫度。

所述的微波電磁損耗模型適用于金屬微波器件，所述金屬微波器件包括波導法蘭、同軸連接器等。

本發明的溫度場還會影響微波電磁損耗模型的材料系數。一些材料參數，諸如材料密度ρ、熱容Cp、泊松比μ等對溫度是不敏感的，在溫度變化時可將它們看成常數，通常取常溫時的值。其它的物理參數包括電導率σ、熱導率k、楊氏模量E以及熱膨脹系數α是溫度的函數。

本發明的有益效果是：

本發明能夠分析電磁波在金屬微波器件中傳播時，在腔體表面產生損耗，進而形成熱效應，以致器件在熱應力作用下形變的情況，簡便而準確地計算出溫度的變化以及隨之產生的應力和形變。

附圖說明

圖1為本發明實施例方法的原理示意圖。

圖2是本發明實施例提供的微波電磁損耗模型的示意圖。

圖3是本發明實施例電磁波在器件內部傳播的電場強度分布圖。

圖4是本發明實施例電磁波在器件表面的熱損耗分布圖。

圖5是本發明實施例電磁波在器件內部傳播引起的應力分布圖。

具體實施方式

下面結合本發明實施例中的附圖，詳細描述本發明的實施過程。

本發明的實施例如下：

如圖2所示為微波在器件表面的損耗模型，實施例的平面波沿金屬微波器件長度方向入射到金屬微波器件的內腔中，損耗區域為微波器件內表面。主要分成三個過程：

第一個過程，平面波入射微波器件在其內部形成電磁場分布。假設由器件端口向其內部入射平面波，根據電磁波自由空間傳播得到在微波器件內部的電磁場分布，即麥克斯韋方程組：

電流連續性定理

磁通連續性定理

高斯定理

法拉第定理

廣義安培定理

其中，表示拉普拉斯算子，t表示時間，和分別為電場強度矢量和電位移矢量，和分別為磁感應強度矢量和磁場強度矢量，ρ_v和分別為自由電荷密度和自由電流密度矢量；

另外采用以下由介質特性決定的三個方程，即本構關系，聯立計算得到電位移、磁感應強度和自由電流密度，并同時相應計算獲得磁場強度：

其中，為傳導電流密度，為真空中或氣體中電流密度，ε為介質介電常數，μ為介質磁導率，σ為導體電導率，ρ_v為真空或氣體中荷電粒子的密度，為真空或氣體中荷電粒子的速度。

第二個過程，計算熱場。由于不是完純導體，微波器件內表面也存在一定的電磁場分布，主要存在于趨膚深度的厚度內，電流集中在導體表面，稱為表面電流，可由麥克斯韋方程以及阻抗邊界條件求得，阻抗邊界條件采用以下公式表示：

將其代入電阻性損耗公式即可求得電磁波傳播在微波器件內部產生的熱損耗。

在固體中，實施例采用的熱傳遞方程表示為如下公式：

其中，ρ為密度(kg/m³)，T表示溫度，C_ρ為恒壓下的熱容(J/(kg·K))，為傳導熱通量(W/m²)，k為熱導率(W/(m·K))，Q為熱損耗(W/m³)。

熱傳遞方程包括兩種基本的邊界條件：指定的溫度和指定的熱通量。

第三個過程，用已經計算出的熱損耗為源，求解應力場。

金屬微波器件滿足線彈性材料的條件，實施例的線彈性材料模型用如下所示的方程組來描述，可計算得到熱應變ε_inel：

s-s₀＝C:(ε-ε₀-ε_inel)

ε_inel＝α(T-T_ref)

其中，s表示應力，表示位置，α為熱膨脹系數，T_ref為應變參考溫度，s₀為初始應力，ε為應變張量，ε₀為初始應變，C為彈性張量，:為張量積。上述三個公式分別為應變-位移關系式、Duhamel-Hooke定律以及應力張量與應變張量及溫度的關系。

在金屬微波器件的線彈性材料中，由于材料的對稱性，上述應力張量ε寫成以下的矩陣形式：

其中，ε_x、ε_y和ε_z屬于正應變，ε_xy、ε_yz和ε_xz屬于剪切應變，分別表示張量ε的九個分量。

同理，應力張量s和熱膨脹張量α也寫成類似的矩陣形式，將張量用九個分量表示：

本發明具體實例是以長300mm，寬123.22mm，高68.61mm，波導壁厚度7mm的直波導為例，在其一端輸入25W，2.4GHz的平面波，電場分布在x、z方向上無變化，在y方向上是余弦函數(附圖3)，同樣的，熱損耗在x、z方向上不變，y方向為cos²分布(附圖4)，具體熱損耗函數為：

Q＝[0.347cos(πy/109.22)]^2+0.11

以熱損耗Q為源，在熱應力場中可以求得溫度和應力的變化，波導整體上升了約0.00007K，應力分布有兩種情況(附圖5)，波導內部分布均勻，在110MPa左右，端口處應力主要分布在四個角，最大處約為450MPa。

本發明技術領域涉及的計算涉及大量偏微分方程，較為復雜，多為軟件仿真使用。由于電磁與應力場的耦合影響極小，卻又占據計算大量內存，在工程上完全可以忽略，因此通過本發明方法將原來長達數個小時的計算簡化到半個小時以內，大大提高了效率，精簡了過程，也可減小多步計算的誤差。

以上所述，僅為本發明的具體實施方式，但本發明的保護范圍并不局限于此，任何熟悉本技術領域的技術人員在本發明披露的技術范圍內，可輕易想到的變化或者替換，都應涵蓋在本發明的保護范圍之內。因此，本發明的保護范圍應該以權力要求書的保護范圍為準。