一種基于PMPSD的工業機器人絕對精度校準方法與流程

本發明涉及機器人標定技術領域，特別是涉及一種基于PMPSD(Pose Modify Position Sensitive Detector)的工業機器人絕對精度校準方法。

背景技術：

隨著工業機器人應用領域的擴大和高端制造產業的需求，對工業機器人的性能提出了更高的要求。定位精度是反映機器人綜合性能的一個重要指標，可以分為重復定位精度和絕對定位精度。目前工業機器人的重復定位精度比較高，而其絕對定位精度較低，難以滿足高精度行業(如汽車制造業、電子電氣行業)的生產需求。

工業機器人的定位誤差主要分為幾何誤差和非幾何誤差，其中幾何誤差成為影響工業機器人定位誤差的主要因素。因此，需要利用標定技術對其進行運動學標定，辨識出機器人的幾何參數誤差，并對幾何參數名義值進行修正，從而對機器人的絕對定位精度進行校準。

目前，標定方法可以分為：基于神經網絡補償法、基于插補思想補償法、微分誤差補償法、關節空間補償法。按照建模方式補償又可分為有機理建模和實驗建模兩大類。微分誤差補償法和關節空間補償法是按照機器人的運動學規律補償的一種方式，屬于有機理建模。而神經網絡補償法和插補思想補償法是研究機器人對象，并估算其輸入與輸出的建模方法，屬于實驗建模。

上述研究多為基于高精度測量設備的條件下，對工業機器人末端位姿進行測量，如：激光跟蹤儀、三坐標測量儀、機器人關節臂、拉線式機器人測量和性能分析系統等。而這些設備昂貴，使用時需要耗費大量的時間進行測量系統與機器人基坐標系之間的坐標變換，對操作人員的水平依賴高，主要適合于實驗室場景下研究。

針對設備昂貴、操作復雜等問題，在機器人末端施加約束而形成運動學閉合鏈的方法被提出來。該方法避開了昂貴的設備，并且不需要耗費時間建立測量設備與機器人基坐標之間的轉換關系，同樣避免了坐標轉換誤差。提出了采用一種基于PSD(Position Sensitive Detector)的標定方法，在工業機器人末端安裝激光器，并投射激光束于PSD中心，以構成空間點約束形成閉合運動鏈的方法，通過構建約束目標函數，利用最小化方法辨識出工業機器人的幾何參數誤差。但是該方法存在的問題是，對于精度低的工業機器人很難通過反饋控制，將激光束準確地投射到PSD中心，因此不能準確地采用點約束方法構建正確的約束目標函數，進而不能準確地辨識出工業機器人的幾何參數誤差。

技術實現要素：

本發明目的是針對工業機器人絕對定位精度低，提出一種基于PMPSD的工業機器人絕對精度校準方法。

為了實現上述目的，本發明通過如下技術方案實現：

第一步：建立機器人誤差運動學模型；

第二步：建立空間多點虛擬約束，使用PSD裝置進行數據采樣；

第三步：利用空間矢量關系修正機器人末端激光器的位姿，并利用修正后的位姿對機器人關節轉角進行修正，以取代從機器人示教器或從控制器得到的關節轉角；

第四步：構建模型約束目標函數；

第五步：利用最小化方法對約束目標函數進行優化，得到工業機器人的參數誤差；

第六步：將參數誤差對幾何參數名義值進行修正，實現機器人的絕對精度校準。

根據以上的技術方案，可以實現以下的有益效果：

(1)本發明的基于PMPSD的工業機器人絕對精度校準方法適用于任何串聯關節型機器人及任何平面關節型機器人，方法通用型強；

(2)本發明不需要構建測量儀器與機器人基坐標之間的坐標轉換關系，節省了標定時間，并且避免了坐標轉換帶來的誤差；

(3)本發明所述的參數誤差模型考慮了工業機器人本體的所有幾何參數，將辨識后的參數誤差補償到工業機器人幾何參數名義值中，更接近于實際模型，能夠有效地對工業機器人精度實現校準；

(4)由于采用對激光器位姿修正的方法，不需要將激光束準確投射到PSD中心，避免了采用PSD反饋控制的策略。

附圖說明

圖1本發明所采用PSD裝置進行數據采樣的示意圖；

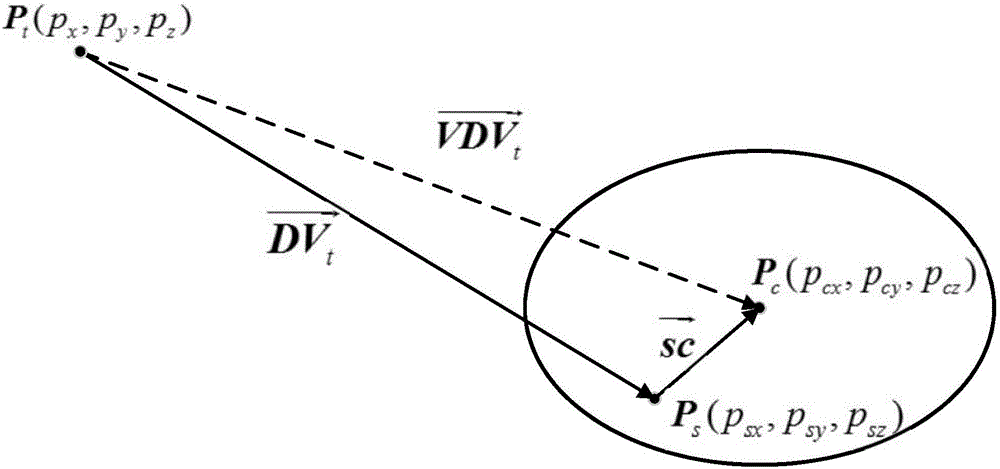
圖2本發明進行激光器末端位姿修正的示意圖；

圖3本發明的具體操作流程。

具體實施方式

為使本發明的目的、技術方案和優點等更加清楚明白，以下結合實施例，并參照附圖，對本發明進一步詳細說明。

一種基于PMPSD的工業機器人絕對精度校準方法，操作流程圖如圖3所示，所述方法包括以下步驟：

第一步：建立機器人誤差運動學模型，包括以下步驟：

步驟(1)，使用D-H規則構建機器人誤差運動學模型。

在D-H規則中，相鄰兩桿之間的運動學關系為：

式中，為連桿i與連桿i-1的運動學關系，其中a_i為連桿長度，Δa_i為連桿長度誤差，d_i為連桿偏距，Δd_i為連桿偏距誤差，α_i為關節扭角，Δα_i為連桿扭角誤差，θ_i為關節轉角，Δθ_i為關節轉角誤差。其中，幾何參數誤差Δs＝[Δa₁ Δd₁ Δα₁ Δθ₁ … Δa_n Δd_n Δα_n Δθ_n]^T，Δs為m×1的矩陣，m為待辨識的參數個數，n為機器人關節數。

步驟(2)，利用工具坐標系標定方法對安裝在機器人末端的激光器進行標定，得到激光器相對于機器人末端關節的坐標關系因此得到機器人的基坐標到激光器之間的總變換為：

其中，n為機器人關節數，如對于一個六自由度的機器人而言，對應著6個齊次變換矩陣。

第二步：建立空間多點虛擬約束，使用PSD裝置進行數據采樣。

使用PSD裝置進行數據采樣，包括以下步驟：

步驟(1)，由于參數誤差的存在，激光束很難準確投射到PSD中心點，本方法只需要將激光束投射到PSD表面即可。將PSD裝置放置在激光束可投射的空間中，機器人以任意姿態將激光束投射到PSD表面，此時記錄激光束投射在PSD上的斑點位置P_s，i，j，并從機器人示教器或直接從控制器中讀取關節轉角值θ_i，j，其中i＝1，2…k，j＝1，2…m，k為同一PSD裝置位置的數據采樣次數，m為PSD裝置的位置個數。

步驟(2)，改變機器人的位姿，重新將激光束投射到PSD表面，依照步驟(1)重復k次，因此可以獲得k組激光束投射在PSD表面的斑點位置P_s，i，j以及k組不同姿態下的關節轉角值θ_i，j，其中i＝1，2…k，j＝1，2…m，k為同一PSD裝置位置的數據采樣次數，m為PSD裝置的位置個數。

步驟(3)，重新放置PSD裝置的位置，重復步驟(1)和(2)。標定過程中，PSD裝置放置的位置個數為m。

第三步：利用空間矢量關系修正機器人末端激光器的位姿，并利用修正后的位姿對機器人關節轉角進行修正，以取代從機器人示教器或從控制器得到的關節轉角。包括以下步驟：

步驟(1)，利用示教器控制方式，將激光束投射到PSD中心，記錄此時的關節轉角θ₁，然后改變機器人位姿，重新將激光束投射到PSD中心，記錄此時的關節轉角θ₂，這時便可得到兩組激光束方程，可求得PSD中心點相對于機器人基坐標系的坐標為P_f(p_fx，p_fy，p_fz)。由于PSD為位置傳感器，因此，當激光束再投射到PSD表面時，此時的斑點位置為P_s(p_sx，p_sy，p_sz)。

步驟(2)，設三維空間中任意一條激光束的直線方程表示為L＝(p_x，p_y，p_z，α，β，γ)，其中P_t(p_x，p_y，p_z)為激光器相對于機器人基坐標系的坐標，為在基坐標系下的激光束方向矢量。由于激光器以不同的位姿將激光束投射到PSD的表面，因此可以得到多組機器人關節轉角，也就可以獲得多組激光束在機器人基坐標系下的直線方程。PSD表面中心點坐標為P_c(p_cx，p_cy，p_cz)，激光束投射在PSD上的斑點位置為P_s(p_sx，p_sy，p_sz)，可得投射斑點到PSD中心點的方向矢量為

步驟(3)，已知激光束方向矢量及投射斑點至PSD中心點的方向矢量如附圖2所示，因此可以得到虛擬激光束方向矢量為

步驟(4)，利用已知激光器坐標P_t(p_x，p_y，p_z)及得到的虛擬激光束方向矢量再運用機器人運動學逆解求得多組關節轉角值，并選取其中完全平方差之和最小的一組關節轉角θ′，將關節轉角θ′取代之前從機器人示教器或控制器取得的關節轉角值θ。

第四步：構建模型約束目標函數。

步驟(1)，求任意兩條激光束直線的交點或者公垂線中點。

令其中兩條激光束直線的方程分別表示：

根據激光束的方程，利用式(5)可求取兩條激光束的交點。然而在實際情況下，兩條激光束的交點并不一定存在，此時需要利用式(7)求取兩條激光束的公垂線中點近似為交點。

1)當兩條激光束直線存在交點時，通過求解其交點坐標為：

P＝(kα₁+px₁，kβ₁+py₁，kγ₁+p_z1) (5)

其中：

2)當兩條激光束直線不存在交點時，則公垂線的中點為：

其中：

步驟(2)，建立空間多點虛擬約束模型。

在建立空間多點虛擬約束模型前，首先需要求取PSD裝置在位置m處時的交點或者公垂線中點的平均值作為該PSD位置下的交點平均值，i＝1，2…m。求取過程只要令機器人的參數誤差為0，在同一PSD位置處k組數據，得到個交點，然后取平均即可。

在空間多點虛擬約束模型中，首先以PSD裝置同一位置處，任意兩條激光束的交點或者公垂線中點到該交點平均值的距離作為約束目標函數，構建空間單點虛擬約束模型，最后將空間單點虛擬約束模型統一構建為空間多點約束模型，所建立的約束目標函數如式(16)所示。

其中，k為同一PSD裝置位置處的數據采樣次數，m表示PSD裝置放置的不同位置的個數。(ⁱx_j，ⁱy_j，ⁱz_j)為在位置i處時的第i個交點或者公垂線中點，為PSD裝置在位置m處時的交點或者公垂線中點的平均值。其中，i＝1，2…m，j＝1，2…K。當m＝1時，模型為構建單點虛擬約束模型。

第五步：利用最小化方法對約束目標函數進行優化，得到工業機器人的參數誤差。

使用最小化方法LM(Levenberg-Marquardt)算法不斷進行迭代使得δ^*最小化，此時工業機器人的參數誤差Δs將會被辨識出來，Δs＝[Δa₁ Δd₁ Δα₁ Δθ₁ … Δa_n Δd_nΔα_n Δθ_n]^T，Δs為m×1的矩陣，m為待辨識的參數個數，n為機器人關節數。步驟如下。

步驟(1)，初始化參數誤差Δs，LM算法的初始化相關參數，迭代次數k；

Δs₀＝0，μ＝0.1，v＝2，k＝1 (17)

步驟(2)，計算第k次迭代時的雅可比矩陣J(Δs_k)；

雅克比矩陣J(Δs_k)由Ω對Δs分量求解偏微分得到，其中Ω＝[Ω₁，Ω₂，…Ω_k×m]，

步驟(3)，利用LM算法求解參數誤差矩陣h_lm；

h_lm＝-(J(Δs_k)^TJ(Δs_k)+μ×I_m×m)^-1J(Δs_k)^TΩ (18)

其中h_lm表示為第k次迭代時參數誤差的改變值，為m×1矩陣，Δs_k為第k次迭代時的參數誤差，為m×1矩陣，μ為阻尼因子，m為待辨識的參數個數。

步驟(4)，計算第k次迭代時實際下降量^AD_k與預估下降量^PD_k的比值ρ；

^AD_k＝F(Δs_k)-F(Δs_k+h_lm) (19)

步驟(5)，更新迭代參數；

若ρ＞0：

Δs_k＝Δs_k+h_lm (22)

v＝2 (24)

否則：

μ＝μ×v (25)

v＝2×v (26)

重復步驟(2)至(5)。當||J(Δs_k)^TΩ||＜ε時，循環結束，得到最終的機器人參數誤差Δs＝Δs_k，否則k＝k+1。

第六步：將辨識出的參數誤差對幾何參數名義值進行修正，實現機器人的絕對精度校準。辨識出的參數誤差為Δs，s_g＝s_n+Δs，s_n為機器人幾何參數名義值，s_g為機器人幾何參數真實值。