基于柔性胎架的船舶曲面分段定位方法與流程

本發明涉及的是一種船舶三維裝配領域的技術，具體是一種基于柔性胎架的船舶曲面分段定位方法。

背景技術：

造船通常采用分段式建造的方法，船舶曲面分段是船舶殼體的主要組成部分，其重量大，體積龐大，輪廓彎曲結構復雜，裝配定位困難。柔性胎架可以對曲面分段進行定位，要求在工藝設計過程中對數控胎架系統進行設計。但柔性胎架的調節精度有限，對曲面分段的姿態沒有進行優化，也無法保證曲板構件穩定性達到最高。

技術實現要素：

本發明針對現有技術沒有對曲面分段的定位姿態進行優化，或沒有對多胎架組合使用的情況進行計算等局限，導致無法保證曲板構件穩定性達到最高以及使用的模型為理想設計，與實際產品存在差異，因此在進行胎架支柱高度計算時容易定位誤差等等缺陷，提出一種基于柔性胎架的船舶曲面分段定位方法。

本發明是通過以下技術方案實現的：

本發明根據船舶殼體的網格模型中曲面分段的各個姿態的重心高度，得到重心高度最小時的姿態作為定位姿態，從而計算得到柔性胎架的優化使用數量，并進一步根據柔性胎架的支撐桿與曲面分段碰撞模型確定各個支撐桿的上升行程，實現模型的優化以提高定位精度。

所述的網格模型，為曲面分段的STL格式三角網格模型。

所述的重心高度是指：曲面分段質心的z方向分量與曲面分段最低點的z方向分量之差。

所述的定位姿態，通過以下方式得到：

1)在三角網格模型中，計算每個三角面片三個頂點的坐標得到坐標矩陣T＝{P₁,P₂,P₃}，并計算該三角面片的法向量

2)建立世界坐標系oxyz，得到曲面分段的位姿矩陣M_q；

3)構造曲面分段旋轉后的旋轉位姿矩陣M_qij＝M_ix×M_jy×M_q，其中：M_ix為曲面分段繞x軸旋轉i度的旋轉矩陣，M_jy為曲面分段繞y軸旋轉j度的旋轉矩陣，i和j都為[-90,90]中的整數；

4)計算各個旋轉位姿矩陣M_qij下的曲面分段的質心z方向分量m_zqij以及曲面分段最低點z方向分量P_{z min ij}，得到旋轉位姿矩陣M_qij對應的重心高度H_ij＝m_zqij-P_{z min ij}；

5)重心高度最小值所對應的旋轉位姿矩陣作為定位姿態M_{q min}。

所述的優化使用數量，通過以下方式得到：

①曲面分段的質心z方向分量其中：l為曲面分段中的各個三角面片編號，m_lTz為三角面片與其xoy平面投影組成的五面體的質心z方向分量，σ_lT為三角面片的法向因子且

②在定位姿態下，遍歷曲面分段中所有三角面片頂點，得到x、y方向最大和最小坐標值x_min、x_max、y_min、y_max；

③計算柔性胎架數量Num＝Num_x×Num_y，其中：W_T為柔性胎架的寬度。

所述的上升行程，通過以下方式得到：首先生成各個支撐桿與曲面分段的碰撞模型，并以固定步長將支撐桿的最大上升距離離散化，再判斷支撐桿當前位置與曲面分段是否發生碰撞，當發生碰撞時則此時上升距離為支撐桿上升行程，當不發生碰撞時則判斷支撐桿的上升行程是否為最大行程，如是則支撐桿無需移動，否則支撐桿上升一個步長并重復判斷是否發生碰撞，最終得到確定的上升行程。

技術效果

與現有技術相比，本發明根據重心最低原則計算并得到曲面分段定位時的最穩定姿態；根據曲面分段的形狀與定位姿態自動計算柔性胎架的數量；將實際胎架支撐柱的三維模型用于碰撞檢測計算中，具有較高的定位精度。

附圖說明

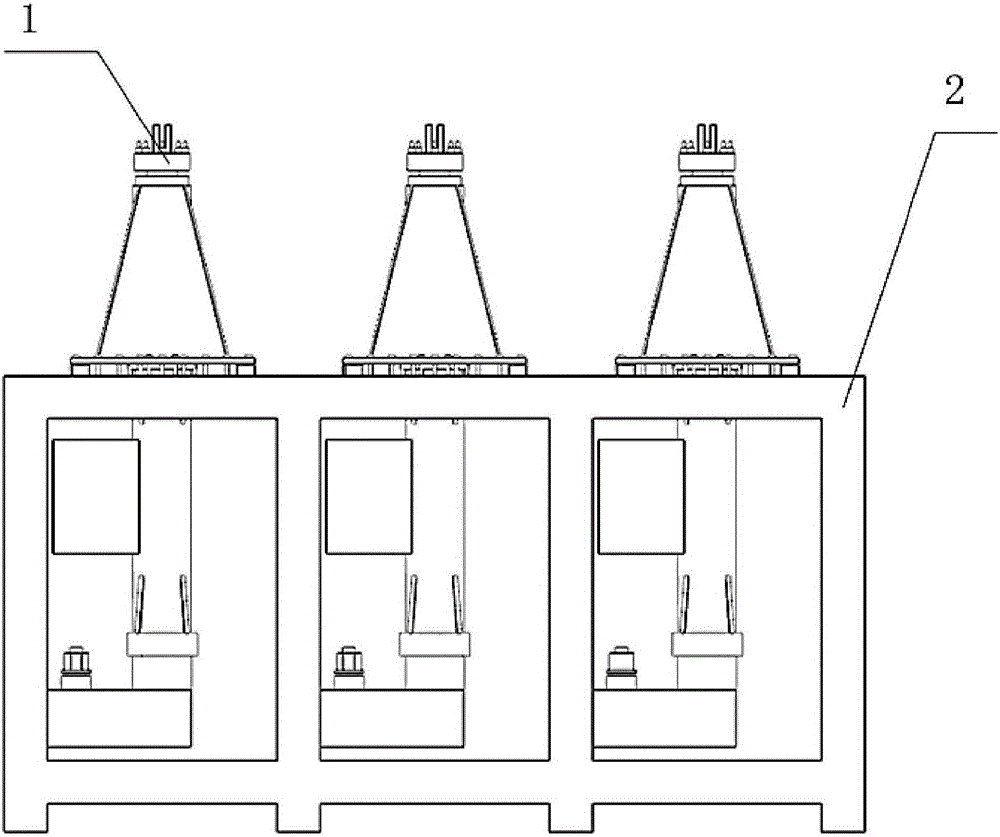
圖1為柔性胎架結構示意圖；

圖2為本發明流程示意圖；

圖3為重心高度計算流程示意圖；

圖4為五面體位置示意圖；

圖5為上升行程計算流程示意圖；

圖中：1支撐桿、2底座。

具體實施方式

下面對本發明的實施例作詳細說明，本實施例在以本發明技術方案為前提下進行實施，給出了詳細的實施方式和具體的操作過程，但本發明的保護范圍不限于下述的實施例。

實施例1

如圖1所示，本實施例所用的每個柔性胎架具有9個支撐桿1，支撐桿1設置于底座2，底座2為方形，邊長為3000mm。

如圖2所示，本實施例中的船舶曲面分段定位方法包括以下步驟：

1)建立曲面分段的三角網格模型。使用常用的軟件打開曲面分段的模型文件，然后導出ASCII碼格式的STL模型即為三角網格模型，精度設置為0.1mm。

2)如圖3所示，在世界坐標系oxyz中，計算曲面分段各個姿態的重心高度H，以重心高度最小的姿態作為定位姿態。

2.1)在三角網格模型中，計算每個三角面片三個頂點P₁、P₂、P₃的坐標得到坐標矩陣T＝{P₁,P₂,P₃}，并計算三角面片的法向量P₁＝[x₁,y₁,z₁]^T，P₂＝[x₂,y₂,z₂]^T，P₃＝[x₃,y₃,z₃]^T。

2.2)建立世界坐標系oxyz，得到曲面分段的位姿矩陣M_q。在曲面分段的定位空間中建立一個世界坐標系，坐標原點為o，x、y、z軸方向分別為正東、正北以及垂直地面向上方向。計算曲面分段在裝配工作時的初始的位姿矩陣M_q，M_q為一4×4矩陣以表示曲面分段在世界坐標系下的姿態。

2.3)構造曲面分段旋轉后的旋轉位姿矩陣M_qij＝M_ix×M_jy×M_q，其中：M_ix為繞x軸旋轉i度的旋轉矩陣，M_jy為繞y軸旋轉j度的旋轉矩陣，i和j都為-90到90整數，i和j組合得到32761組M_qij。

如圖4所示，所述的三角面片的各個頂點也同時轉化為在世界坐標系下的坐標即P_w＝P×M_qij，將三角面片的三個頂點向xoy平面作垂線，得到一個五面體P_1wP_2wP_3wP_1w′P_2w′P_3w′。

2.4)計算各個旋轉位姿矩陣M_qij下的曲面分段的質心z方向分量m_zqij以及曲面分段最低點z方向分量P_{z min ij}，得到旋轉位姿矩陣M_qij對應的重心高度H_ij＝m_zqij-P_{z min ij}。計算每一個三角面片構成的五面體P_1wP_2wP_3wP_1w′P_2w′P_3w′的質心的z方向分量。

所述的曲面分段的質心z方向分量其中：l為曲面分段中的各個三角面片編號，m_zlT為三角面片與其xoy平面投影組成的五面體P_1wP_2wP_3wP_1w′P_2w′P_3w′的質心z方向分量，σ_lT為三角面片的法向因子且而后得到旋轉位姿矩陣M_qij對應的重心高度H_ij＝m_zqij-P_{z min ij}。此時，得到32761個重心高度H_ij。

2.5)重心高度最小值所對應的旋轉位姿矩陣作為定位姿態M_{q min}。在32761個重心高度H中選取最小值，其對應的旋轉位姿矩陣即為定位姿態M_{q min}。

3)根據曲面分段的三角網格模型和定位姿態計算柔性胎架的使用數量。

3.1)在定位姿態下，遍歷曲面分段中所有三角面片頂點，得到x、y方向最大和最小坐標值x_min、x_max、y_min、y_max；

3.2)計算柔性胎架數量Num＝Num_x×Num_y，其中：W_T為柔性胎架的寬度。代入具體數值，因此Num_x＝13，此時Num_y＝19。所以，需要247個柔性胎架。

4)如圖5所示，建立柔性胎架的支撐桿與曲面分段碰撞模型以進而確定各個支撐桿的上升行程。

4.1)生成各個支撐桿與曲面分段的碰撞模型，使用CDMake文件生成碰撞模型，其中碰撞精度為0.1mm。

4.2)以固定步長將支撐桿的最大上升距離離散化。支撐桿的最大上升距離S_max為500mm，固定步長取0.1mm，支撐桿在各個上升距離的位姿表示為M_Z。

4.3)支撐桿當前位置與曲面分段碰撞則此時上升距離為支撐桿上升行程，否則進行下一步驟；

4.4)支撐桿的上升行程為最大行程則支撐桿無需移動，否則支撐桿上升一個步長并回到步驟4.3)，即從新計算新的上升距離下的M_Z并計算是否碰撞。

對所有支撐桿通過步驟4)獲得其上升行程，并生成數控文件，即可用于柔性胎架的控制。

與現有技術相比，本發明根據重心最低原則計算并得到曲面分段定位時的最穩定姿態；根據曲面分段的形狀與定位姿態自動計算柔性胎架的數量；將實際胎架支撐柱的三維模型用于碰撞檢測計算中，具有較高的定位精度。