一種考慮碳稅的電力系統經濟調度方法與流程
本發明涉及電力系統調度與管理領域,具體涉及一種考慮碳稅的電力系統經濟調度方法。
背景技術:
碳稅是對二氧化碳排放所征的稅,作為一種減少二氧化碳排放的有效措施,碳稅在全世界范圍內得到廣泛應用。電力系統是最大的二氧化碳排放源之一,降低碳排放是未來電力系統運行中需要考慮的重要因素。傳統的經濟調度以系統發電成本最小為目標,沒有考慮系統排放造成的外部成本。將碳稅考慮進電力系統經濟調度模型,可以將排放的二氧化碳造成的外部成本內化為系統運行的經濟指標,與發電成本進行統一優化,能夠實現經濟與環境的統一最優,降低用戶最終的用電成本。
技術實現要素:
本發明的目的在于針對現有技術的不足,提供一種考慮碳稅的電力系統經濟調度方法。
本發明的目的是通過以下技術方案來實現的:一種考慮碳稅的電力系統經濟調度方法,該方法包括以下步驟:
(1)建立用戶碳稅成本模型,具體為:
(1.1)確定負荷的碳排放強度ELj;
(1.2)確定用戶的碳稅成本:將負荷的碳排放強度ELj與負荷量PLj乘積作為該負荷引起的碳排放量,將所有負荷碳排放量與碳稅Tj的乘積之和作為用戶總的碳稅成本fC。即:Nl為系統內負荷的個數。
(2)建立經濟調度模型,具體為:
(2.1)確定目標函數:以系統總的發電成本和用戶總的碳稅之和為目標函數,即Minf=fG+fC,其中fG為所有發電機的發電成本之和。
(2.2)確定約束條件:功率平衡約束、支路功率約束、節點電壓幅值約束、發電機出力約束。
(3)求解經濟調度模型:利用原對偶內點法對經濟調度模型進行求解,確定每臺發電機的有功和無功出力計劃。
進一步地,所述步驟(1)建立用戶碳稅成本模型中,確定負荷的碳排放強度ELj是指:
a.確定每臺發電機組的碳排放強度EGi;
b.利用潮流追蹤技術,確定確定每個用電負荷的電力來源,將發電機-負荷分配系數矩陣表示為A,Aij表示第i臺發電機對第j個負荷的分配系數。所有發電機對第j個負荷的分配系數之和為1,即其中Ng為發電機個數;
c.確定負荷的碳排放強度:將負荷的碳排放強度設為所有向該負荷供電的發電機碳排放強度的加權平均值,即:
進一步地,所述步驟(1)建立用戶碳稅成本模型中,確定負荷的碳排放強度ELj,ELj是取決于發電機輸出的變量。
進一步地,所述步驟(2)建立經濟調度模型,該模型具體是指:
①目標函數:
Minf=fG+fC
②約束條件:
A.功率平衡約束:
其中,PGi,QGi,PDi,QDi分別為節點i上發電機輸出的有功功率、無功功率和節點i上負荷的有功功率、無功功率。θi和|Vi|分別為節點i電壓的相角和幅值,Gij和Bij分別為支路i-j的等效電導和電納,Nb為系統節點數。
B.發電機出力約束:
其中,PGi,分別為節點i上發電機輸出有功功率的下限和上限,QGi,分別為節點i上發電機輸出無功功率的下限和上限。
C.支路功率約束:
|Sij|≤|Sij|max
其中,|Sij|為支路i-j的的視在功率,|Sij|max為支路i-j的視在功率的上限。
D.節點電壓幅值約束:
|Vi|min≤|Vi|≤|Vi|max
其中,|Vi|min,|Vi|0ax分別為節點i電壓幅值的下限和上限。
進一步地,步驟(3)利用原對偶內點法求解經濟調度模型,需要求目標函數對變量的一階導和二階導。同時,在步驟(1)利用潮流追蹤技術確定的發電機-負荷分配系數矩陣A中會出現逆矩陣Z-1。在求解過程中,將對Z-1的求導問題轉換為對原矩陣Z的求導問題:
其中,xp為經濟調度模型中的變量。
本發明的優點和積極效果是:
1、本發明將潮流追蹤中出現的逆矩陣求導問題轉化為對原矩陣的求導問題,因此可以將潮流追蹤確定的用戶碳稅加入經濟調度的目標函數中,實現了對發電成本和碳稅成本的聯合優化。
2、本發明方法中,經濟調度模型中考慮了用戶負荷對電價的彈性,用戶負荷既可以是固定負荷也可以是取決于電價水平的靈活負荷。因此,當碳排放強度高的發電機(如低效率的火電機組)發電較多時,系統成本較高,用戶可以降低其負荷需求量。反之,當清潔電源發電較多時,系統成本相對較低,用戶可以提高其負荷需求量。通過這種方式,鼓勵了電力用戶參與節能減排,實現了降低用戶碳排放強度以及用戶電能費用的目的。
附圖說明
圖1為本發明方法流程圖;
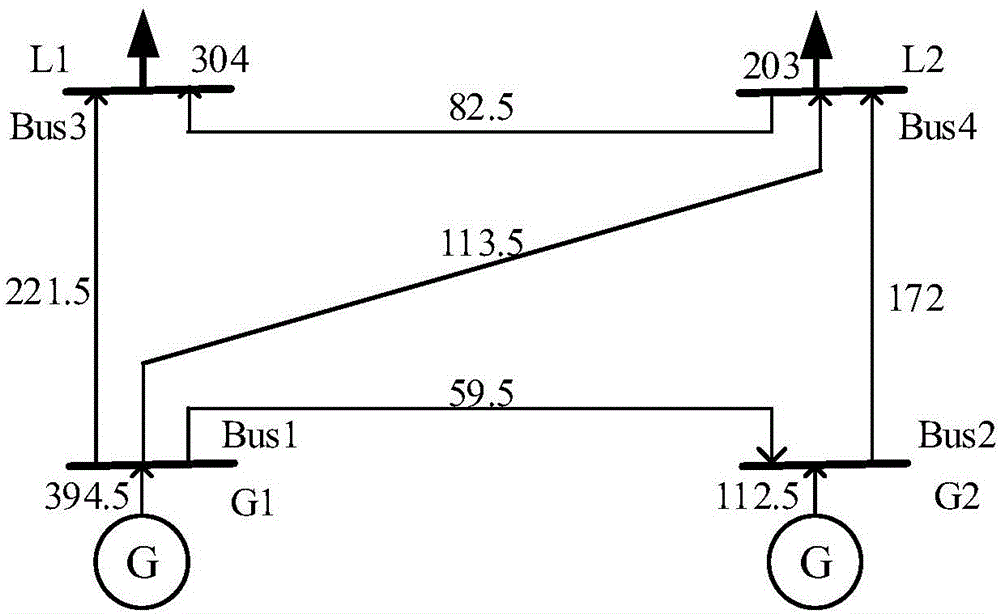
圖2為對四節點電力系統中的四節點進行潮流追蹤的結果示意圖。
具體實施方法
下面結合附圖和具體實施例對本發明作進一步詳細說明。
如圖1所示,本發明提供的一種考慮碳稅的電力系統經濟調度方法,該方法包括以下步驟:
(1)建立用戶碳稅成本模型,具體為:
(1.1)確定負荷的碳排放強度ELj:
a.確定每臺發電機組的碳排放強度EGi;
b.利用潮流追蹤技術,確定確定每個用電負荷的電力來源,將發電機-負荷分配系數矩陣表示為A,Aij表示第i臺發電機對第j個負荷的分配系數。所有發電機對第j個負荷的分配系數之和為1,即其中Ng為發電機個數;
c.確定負荷的碳排放強度:將負荷的碳排放強度設為所有向該負荷供電的發電機碳排放強度的加權平均值,即:
以四節點電力系統為例,對四節點進行潮流追蹤的結果如圖2所示。
發電機-負荷的功率流向可以用發電機-負荷貢獻因子矩陣A表示為:
根據圖2的結果,得到:
因此:
EL1=0.6882×EG1+0.2890×EG2
EL2=0.3118×EG1+0.7110×EG2
(1.2)確定用戶的碳稅成本:將負荷的碳排放強度ELj與負荷量PLj乘積作為該負荷引起的碳排放量,將所有負荷碳排放量與碳稅Tj的乘積之和作為用戶總的碳稅成本fC。即:Nl為系統內負荷的個數。
(2)建立經濟調度模型,具體為:
(2.1)確定目標函數:以系統總的發電成本和用戶總的碳稅之和為目標函數,即Min f=fG+fC,其中fG為所有發電機的發電成本之和。
(2.2)確定約束條件:功率平衡約束、支路功率約束、節點電壓幅值約束、發電機出力約束。
A.功率平衡約束:
其中,PGi,QGi,PDi,QDi分別為節點i上發電機輸出的有功功率、無功功率和節點i上負荷的有功功率、無功功率。θi和|Vi|分別為節點i電壓的相角和幅值,Gij和Bij分別為支路i-j的等效電導和電納,Nb為系統節點數。
B.發電機出力約束:
其中,PGi,分別為節點i上發電機輸出有功功率的下限和上限,QGi,分別為節點i上發電機輸出無功功率的下限和上限。
C.支路功率約束:
|Sij|≤|Sij|max
其中,|Sij|為支路i-j的的視在功率,|Sij|max為支路i-j的視在功率的上限。
D.節點電壓幅值約束:
|Vi|min≤|Vi|≤|Vi|max
其中,|Vi|min,|Vi|max分別為節點i電壓幅值的下限和上限。
(3)求解經濟調度模型:利用原對偶內點法對經濟調度模型進行求解,確定每臺發電機的有功和無功出力計劃。利用原對偶內點法求解經濟調度模型,需要求目標函數對變量的一階導和二階導。同時,在步驟(1)利用潮流追蹤技術確定的發電機-負荷分配系數矩陣A中會出現逆矩陣Z-1。在求解過程中,將對Z-1的求導問題轉換為對原矩陣Z的求導問題:
其中,xp為經濟調度模型中的變量。
具體如下:
上述經濟調度模型,可以表述為一通用最優模型:
min f(x)
s.t.g(x)=0
h(x)≤0
拉格朗日函數為:
其中,Z為松弛變量向量,Zm為Z中的元素,ni為不等式約束的數量,λ,μ分別為對應等式約束和不等式約束的拉格朗日乘子,γ為障礙因子。
根據KKT條件,當達到最優時,有拉格朗日函數對各變量的一階導為零,即:
用牛拉法求解KKT條件表達式,得到最優解。
- 還沒有人留言評論。精彩留言會獲得點贊!