轉位機構捕獲連接裝置連接過程動力學建模方法與流程
本發明涉及一種動力學建模方法,具體講是一種轉位機構捕獲連接裝置連接過程動力學建模方法,屬于空間站在軌服務技術領域。
背景技術:
空間站轉位機構捕獲連接裝置能夠用于大型航天器與空間站對接后在軌運行所需的組裝、對接和分離等操作活動,是載人航天的重要組成部分之一。轉位機構由旋轉臂和旋轉基座組成。旋轉臂安裝于待轉艙體上,轉位基座安裝于空間站節點艙上,兩者能實現對接、鎖緊、解鎖與復位。轉臂捕獲頭與轉位基座連接過程的動力學與運動學特性復雜,當導向瓣發生接觸后,存在空間上的運動約束。常規的基于牛頓力學的建模方法不能直接應用于含有滑動約束的運動過程建模,制約了轉位機構捕獲連接裝置的研究發展。
技術實現要素:
本發明所要解決的技術問題在于克服現有技術缺陷,提供一種能夠準確描述轉位機構捕獲連接裝置在連接過程中各組成部分之間相互作用下的動力學關系的建模方法。
為了解決上述技術問題,本發明提供的轉位機構捕獲連接裝置連接過程動力學建模方法,包括以下步驟:
步驟1:確定轉位機構捕獲連接裝置的結構和參數,所述轉位機構捕獲連接裝置包括捕獲頭、捕獲桿和轉位基座,所述捕獲頭與捕獲桿相連接,所述捕獲頭與轉位基座可相對移動;所述捕獲頭端面的導向裝置與轉位基座均為圓環形結構,沿外周向均勻間隔設有3個向外展開的梯形導向瓣,捕獲頭與轉位基座之間各導向瓣的位置一一對應;
步驟2:確定連接過程中捕獲頭與轉位基座之間相互接觸滑移的運動約束;
步驟3:確定捕獲頭與轉位基座之間的接觸點在轉位機構捕獲連接裝置上的相對滑移速度;
步驟4:根據步驟2和3確定捕獲頭與轉位基座連接過程的約束動力學方程;
步驟5:解析約束動力學方程。
本發明中,所述步驟2為:設捕獲頭與轉位基座接觸時,第i個接觸點的絕對速度分別為:
其中,表示捕獲頭的第i個接觸點的絕對速度,表示轉位基座的第i個接觸點的絕對速度,ω1表示捕獲頭導向瓣相對于捕獲頭連接面坐標系的旋轉角速度,ω2表示轉位基座導向瓣在轉位基座連接面坐標系內的旋轉角速度,ω3表示由捕獲頭連接面與轉位基座連接面所構成的局部坐標系相對于慣性系的旋轉角速度,捕獲頭連接面中心到第i個接觸點的位置矢量,轉位基座連接面中心到第i個接觸點的位置矢量;表示捕獲頭與轉位基座導向瓣在接觸點1,3的絕對速度,表示捕獲頭與轉位基座導向瓣在接觸點2,4的絕對速度。
本發明中,所述步驟3為:當捕獲頭邊緣g7,q7均為順時針方向時,
其中,分別表示與捕獲頭和轉位基座相關的變量,其中下標數字表示接觸的邊緣;
因此,第i個接觸滑移點速度約束方程為:
其中,表示捕獲頭連接面坐標系相對于捕獲頭連接面與轉位基座坐連接面構成的局部坐標的旋轉角速度,表示捕獲頭與轉位基座在第2個接觸點的絕對速度,表示轉位基座導向瓣在轉位基座連接面坐標系內的旋轉角速度;
捕獲頭的導向瓣與基座第i個接觸點的加速度約束為:
本發明中,所述步驟4為:
其中,m1表示轉臂的質量,m2表示轉位基座所在機構的質量,m3表示轉臂捕獲頭的質量,m4表示轉位基座的質量,AI1表示慣性系向捕獲頭連接面坐標系轉換的旋轉矩陣,A1I表示捕獲頭連接面坐標系向慣性系轉換的旋轉矩陣,m表示接觸點的個數,第i個接觸點的約束力,表示轉臂在慣性系下的等效張量矩陣、表示捕獲頭與轉位基座在接觸點1處的加速度、捕獲頭導向瓣與轉位基座導向瓣在接觸點1,3接觸處的加速度、AI3表示慣性系向局部坐標系變換的旋轉矩,為捕獲頭與轉位基座之間的作用力、A1I捕獲頭連接面坐標系向慣性系變換的旋轉矩陣、為捕獲頭與轉位基座之間的作用力矩、A3I表示局部坐標系向慣性系變換的旋轉矩陣,表示捕獲頭與轉位基座在接觸點2處的加速度,A24表示轉位基座連接面坐標系向慣性系變換的轉換矩陣、A42表示慣性系變換向基座連接面坐標系的轉換矩陣,A2I同A24,Fctrl為作用在轉位基座上的主動控制力,pi為轉位基座與捕獲頭在e3坐標系內描述的位置矢量,ai為轉位基座與捕獲頭之間接觸點在e4坐標系內秒速的矢量位置,I3轉位基座在e3坐標系內描述的等效慣性張量,I1為轉位基座在e1坐標系內描述的等效慣性張量。
5、根據權利要求1至4任一項所述的轉位機構捕獲連接裝置連接過程動力學建模方法,其特征在于所述步驟5為:
步驟51:將步驟4捕獲頭與轉位基座的約束動力學方程設為矩陣:
其中,M表示捕獲頭與轉位基座連接后所形成整體的質量、AT約束方程系數的轉置矩陣;
捕獲頭與轉位基座之間的接觸滑移的運動約束,
式中,為整個系統位形坐標一階倒數列陣,F表示轉位基座與捕獲頭之間的約束力,f=(f1,f2…fm)為捕獲頭與轉位基座的接觸約束力,A為約束方程系數矩陣;
步驟52:構造約束動力學方程的A矩陣的正交補矩陣:
G=ATA (14)
式中,AT為A的轉置矩陣,由式(9)可得G為n×n方陣,其秩為m;
由|λΕ-G|=0得到G的特征值,利用該特征值構造矩陣
式中,Ε表示矩陣G的特征值,C’和C分別表示由非零特征值所對應特征向量和零特征值所對應特征向量所構成的矩陣,矩陣L滿秩
δX=LδZ (16)
其中,δX和δZ之間存在一個單值一一對應關系,由此
因為C矩陣的每一列分別是由矩陣G的特征值的特征向量組成,因此
GC=0 (18)
代入(14)式
由此可以得到
AC=0 (20)
矩陣C即為矩陣A的正交補矩陣,因此方程(19)中的δZ”取任意值均成立,有
把(16)式可寫成
δX=CδZ” (22)
把(22)式代入(12)式可得
結合δZ”的任意性可得
約束動力學的正交補方程組為
本發明將轉位機構捕獲連接裝置的動力學模型簡化為由三個個體組成的多體系統,即捕獲頭、捕獲桿和轉位基座。在建立動力學模型時,考慮捕獲頭與轉位基座之間的接觸滑移約束的復雜性和不確定性,將捕獲頭與轉位基座分開考慮,將接觸點的約束力作為外力分別作用與捕獲頭和轉位基座連接面上。此外,不考慮導向瓣在校正過程中的彈性變形,并利用虛功原理(Jourdain-Bertrand原理),對轉位機構捕獲連接裝置的連接過程進行動力學建模。
本發明的有益效果在于:(1)、將轉位機構捕獲連接裝置連接過程復雜的運動模態,轉化成了空間任意運動的直線與直線之間以及直線與支架之間相互接觸滑動的運動形式,極大的降低了轉位機構捕獲連接裝置連接過程動力學分析的難度;(2)、通過分析上述兩種運動模態的運動約束,給出了其相互接觸點的相對滑移速度的解析表達式,解決了轉位機構捕獲連接裝置在連接過程動力學特性的解析描述。
附圖說明
圖1為轉位機構捕獲連接裝置結構示意圖;
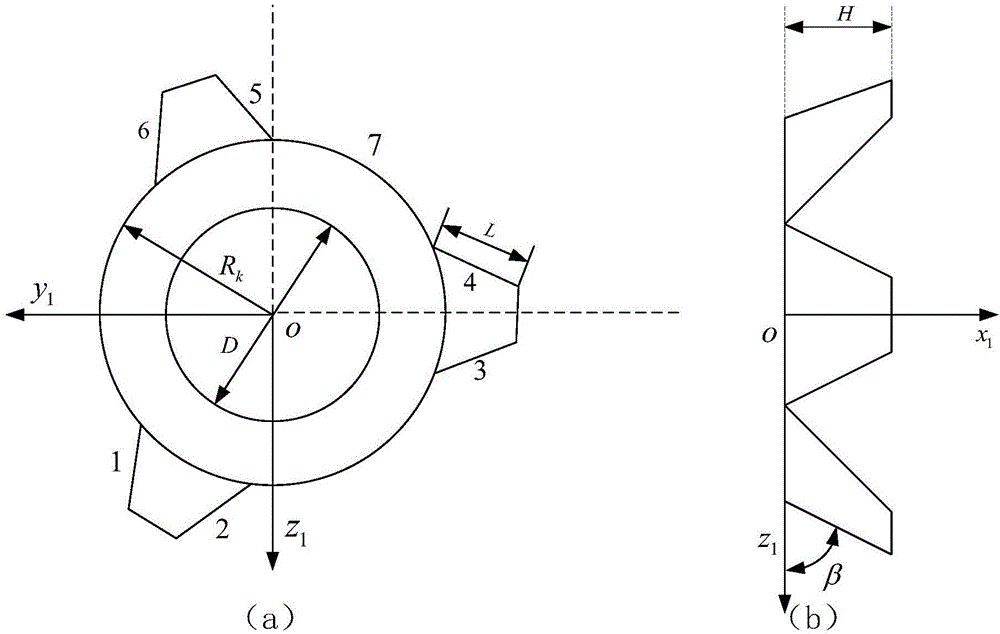
圖2為捕獲頭端面導向裝置結構示意圖;(a)為俯視圖、(b)為側視圖;
圖3為轉位機構基座結構示意圖;(a)為俯視圖、b)為側視圖。
具體實施方式
下面結合附圖對本發明作進一步詳細說明。
如圖1所述,本發明轉位機構捕獲連接裝置連接過程動力學建模方法中采用的轉位機構捕獲連接裝置捕獲頭12、捕獲桿11和轉位基座14。捕獲頭12與捕獲桿11相連接,捕獲頭12的前端面安裝導向裝置13,捕獲頭12與轉位基座14可相對移動,并進行接觸。導向裝置13和轉位基座14的外周安裝向外展開的導向瓣14。
如圖2所示,本發明捕獲頭的導向裝置為圓環形結構,捕獲頭的導向裝置沿外周向均勻間隔設有3個向外展開的導向瓣,導向瓣為梯形結構。捕獲頭導向裝置坐標系e1,圖中D為導向裝置內環直徑,Rk為導向裝置外環半徑,β為導向瓣相對于導向裝置端面的安裝角,H為導向瓣高度,L為導向瓣長度。捕獲頭導向裝置的導向瓣邊緣編號依次為1,2,3,…6,端面邊緣的編號7。圖中,x1、y1和z1表示捕獲頭連接面坐標系的方向。
如圖3所示,本發明轉位基座與捕獲頭的導向裝置的結構一致,其為坐標系e2(即表示轉位基座連接面坐標系)。轉位基座上的3個導向瓣與捕獲頭導向裝置上3個導向瓣的位置一一相對應。轉位基座上的導向瓣邊緣編號依次為1,2,3,…6,端面邊緣的編號7。圖中,x2,y2和z2表示轉位基座連接面坐標系。
本發明轉位機構捕獲連接裝置連接過程動力學建模方法的具體步驟如下:
步驟1:確定轉位機構捕獲連接裝置的結構和結構參數,具體結合及附圖1-3。
步驟2:確定連接過程中捕獲頭與轉位基座之間相互接觸滑移的運動約束:當轉位機構捕獲連接裝置的捕獲頭與轉位基座在捕獲連接過程中,捕獲頭與轉位基座鎖定并回收后,由于導向瓣的結構特點使得接觸點向減小捕獲頭和轉位基座之間相對位置和姿態偏差的方向滑動。因此,建立這種接觸約束條件下的動態約束是建立轉位機構捕獲連接裝置捕獲連接過程動力學模型的首要前提。
根據轉位機構捕獲連接裝置的結構特點,將捕獲頭與轉位基座導向瓣與導向瓣之間的接觸約束,簡化為空間兩條運動直線的相互接觸滑移。假設捕獲頭與轉位基座接觸時,第i個接觸點的絕對速度分別為:
其中,和分別表示捕獲頭與轉位基座的第i個接觸點的絕對速度,ω1表示捕獲頭導向瓣相對于捕獲頭連接面坐標系的旋轉角速度,ω2表示轉位基座導向瓣在轉位基座連接面坐標系內的旋轉角速度,ω3表示由捕獲頭連接面與轉位基座連接面所構成的局部坐標系相對于慣性系的旋轉角速度,捕獲頭連接面中心到第i個接觸點的位置矢量,轉位基座連接面中心到第i個接觸點的位置矢量;表示捕獲頭與轉位基座導向瓣在接觸點1,3的絕對速度,表示捕獲頭與轉位基座導向瓣在接觸點2,4的絕對速度。
步驟3:確定約束接觸點在轉位機構捕獲連接裝置上的相對滑移速度:
當捕獲頭邊緣g7,q7均為順時針方向時,
其中,分別表示與捕獲頭和基座相關的變量,其中下標數字表示接觸的邊緣。
因此,第i個接觸滑移點速度約束方程為:
其中,表示捕獲頭連接面坐標系相對于捕獲頭連接面與轉位基座坐連接面構成的局部坐標的旋轉角速度,表示捕獲頭與轉位基座在第2個接觸點的絕對速度;
導向瓣與轉位基座第i個接觸點的加速度約束為:
步驟4:確定轉位機構捕獲連接裝置連接過程動力學方程
其中,m1表示轉臂的質量,m2表示轉位基座所在機構的質量,m3表示轉臂捕獲頭的質量,m4表示轉位基座的質量,AI1表示慣性系向捕獲頭連接面坐標系轉換的旋轉矩陣,A1I表示捕獲頭連接面坐標系向慣性系轉換的旋轉矩陣,m(無下標時)表示接觸點的個數,第i個接觸點的約束力,表示轉臂在慣性系下的等效張量矩陣、表示捕獲頭與轉位基座在接觸點1處的加速度、捕獲頭導向瓣與轉位基座導向瓣在接觸點1,3接觸處的加速度、AI3表示慣性系向局部坐標系變換的旋轉矩,為捕獲頭與轉位基座之間的作用力、A1I捕獲頭連接面坐標系向慣性系變換的旋轉矩陣、第i個接觸點的約束力,為捕獲頭與轉位基座之間的作用力矩、A3I表示局部坐標系向慣性系變換的旋轉矩陣,表示捕獲頭與轉位基座在接觸點2處的加速度,A24表示轉位基座連接面坐標系向慣性系變換的轉換矩陣、A42表示慣性系變換向基座連接面坐標系的轉換矩陣,A2I同A24,Fctrl為作用在轉位基座上的主動控制力,pi為轉位基座與捕獲頭在e3坐標系(即捕獲頭連接面與轉位基座連接面所構成的坐標系)內描述的位置矢量;ai為轉位基座與捕獲頭之間接觸點在e4坐標系(即慣性坐標系)內秒速的矢量位置,I3轉位基座在e3坐標系(即捕獲頭連接面與轉位基座連接面所構成的坐標系)內描述的等效慣性張量,I1為轉位基座在e1坐標系(即捕獲頭連接面坐標系)內描述的等效慣性張量,如圖1所示。
步驟5:確定約束動力學方程的解析形式
將轉位機構的捕獲頭與轉位基座的動力學方程寫成矩陣形式
其中,M表示捕獲頭與轉位基座連接后所形成整體的質量、AT約束方程系數的轉置矩陣;
捕獲頭與轉位基座之間的接觸滑移運動約束,
上式中,為整個系統位形坐標一階倒數列陣,F表示轉位基座與捕獲頭之間的約束力,f=(f1,f2…fm)為捕獲頭與轉位基座的接觸約束力,A為約束方程系數矩陣。由于捕獲頭與轉位基座在捕獲連接過程中,捕獲頭與轉位基座之間相互運動的空間性和空間作業的過程復雜,直接對式(10)和(11)的約束方程組進行求解。本發明運用D’Alembert正交補原理來處理變維約束問題,目的是將原變維動力學方程組轉換為固定的n為位形空間微分方程組進行求解。根據虛功原理對X的虛位位移需滿足:
約束動力學方程需要滿足
AδX=0 (13)
考慮到系統受到動態運動約束,所以X并不獨立,為此需要通過約束方程的A矩陣的正交補矩陣進行求解,首先約束動力學方程A矩陣的正交補矩陣
G=ATA (14)
其中AT為A的轉置矩陣,有由式(9)可得G為n×n方陣,其秩為m。因此,由|λΕ-G|=0可以得到G的特征值,利用特征值構造矩陣
其中,Ε表示矩陣G的特征值,C’和C分別表示由非零特征值所對應特征向量和零特征值所對應特征向量所構成的矩陣。因此矩陣L必定滿秩
δX=LδZ (16)
其中,δZ,δX是構造的矩陣,僅有數學含義,無物理意義,δX和δZ之間存在一個單值一一對應關系,由此
因為C矩陣的每一列分別是由矩陣G的特征值的特征向量組成,因此
GC=0 (18)
代入(14)式
由此可以得到
AC=0 (20)
矩陣C即為矩陣A的正交補矩陣,因此方程(19)中的δZ”取任意值均成立,有
把(16)式可寫成
δX=CδZ” (22)
把上式代入(12)式可得
由于δZ”的任意性,可得
因此,約束動力學的正交補方程組
式(25)即為在n維位形空間描述的約束動力學基本方程,而約束力f已不出現在方程中了。
本發明具體應用途徑很多,以上所述僅是本發明的優選實施方式,應當指出,對于本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以作出若干改進,這些改進也應視為本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!