一種復合材料層合板的非概率時變可靠性求解方法與流程

本發明涉及復合材料層合板結構的可靠性指標求解的技術領域，特別涉及一種復合材料層合板的非概率時變可靠性求解方法，在概率信息不全的情況下，同時考慮時域中可靠性指標的變化過程，對層合板結構時變可靠度模型的合理表征，時變可靠度的精確求解方法的建立與制定。

背景技術：

復合材料以其優越的力學性能，成為國內外學者研究的熱點問題，針對復合材料典型結構，層合板被廣泛應用到航空、航天、船舶、醫療等各個方面，復合材料技術研究的深度與廣度已經成為國家科技發展的重要標桿，因此，針對層合板結構的力學特性分析與設計技術研究具有重要的理論意義與工程實用價值。

然而，工程層合板結構因其自身各向異性等特點，且處于復雜的服役環境中，存在多種不確定源的影響，加工工藝的不可控性、材料屬性的不均勻性、幾何結構的測量模糊性，外部荷載的隨機性等等都會加劇板結構破壞的不確定性，出現概率信息不全的問題，難以用傳統的概率可靠度求解理論進行求解；另一方面，傳統可靠度理論均是針對時間點給出的時點可靠度，而實際情況下，可靠度是一個隨時間變化的過程，并且t時刻之前的任何一個時刻均可能發生結構失效，傳統可靠度分析并沒有考慮前一時段與下一時刻的相關性，因此，時點可靠性并不能完整而精確的描述結構可靠度。由此可見，傳統結構時點可靠性分析及求解方法已經不再適用。綜合上述情況，針對層合板結構，非概率時變可靠度指標求解方法更具有工程應用價值。

技術實現要素：

本發明要解決的技術問題是：克服現有技術的不足，提供一種針對復合材料層合板結構，考慮非概率時變過程的可靠性求解方法。本發明充分考慮實際工程問題中普遍存在的不確定性因素，構建能夠合理表征層合板結構損傷的損傷演化方程，提出考慮區間變量的非概率時變可靠度指標求解方法，所得到的結果更加符合真實情況，工程適用性更強。

本發明采用的技術方案為：一種復合材料層合板的非概率時變可靠性求解方法，該方法實現步驟如下：

第一步：根據層合板結構的材料、載荷屬性：外部載荷σ，損傷因子D，疲勞壽命N，基于損傷力學引入損傷模型推演結構的損傷演化方程的顯式表達，即：

其中，σ為外部載荷，D為損傷因子，D₀為初始損傷因子，N為疲勞壽命，為損傷速率，A,B為由試驗測得的試驗參數，C為損傷指數。

第二步：利用區間向量x∈x_I＝(σ,D_cr)合理表征貧信息、少數據條件下的結構不確定性，于是有：

其中，結構外部載荷σ，結構安全損傷D_cr，可表示為區間變量，上標U代表參量的取值上界，上標L代表參量的取值下界，上標c代表中心值，上標r代表半徑。

第三步：將第二步中的區間變量σ代入到第一步結構損傷擴展速率方程中，引入非概率區間過程理論，建立含不確定變量的擴展速率方程，即：

其中，σ為區間變量，D₀為初始損傷因子，A,B為由試驗測得的試驗參數，C為損傷指數；

第四步：結合區間過程理論，計算第三步中損傷擴展速率方程的損傷半徑及中值，即：

其中，為結構損傷，上標c代表中心值，上標r代表半徑。

第五步：結合應力-強度干涉模型，根據第四步所求得的結構損傷，建立極限狀態函數，并將其離散化：

G(N_i)＝D_cr(N_i)-D(σ,A,B,C,D₀,N_i)

其中，i＝1,2,…,n，D_cr(N_i)為在第N_i次循環的結構安全損傷門檻值，D為在第N_i次循環的結構實際損傷；

第六步：將首次穿越理論、非概率理論與第五步所建立的極限狀態函數相結合，求解層合板結構首次穿越的可能度，即時變可靠度指標：

其中，N表示整個服役周期，D_cr表示結構安全損傷門檻值，Pos{·}表示事件發生的可能性度量，D(σ,A,B,C,D₀,N_i)表示經歷N_i次載荷循環后層合板結構的損傷擴展度，G(N_i)表示安全性校核的極限狀態函數；

本發明與現有技術相比的優點在于：本發明提供了在概率信息不全的情況下，考慮含區間變量作用下的復合材料層合板結構的時變可靠度指標求解新方法，彌補和完善了概率信息不全情況下，傳統概率理論及時點可靠性設計方法的局限性。所構建的時變可靠性分析模型為復合材料層合板結構的時變可靠度求解問題提供了一種新的解決途徑，一方面降低了對樣本信息的依賴性，另一方面將非概率時變可靠性求解理論與首次穿越理論相結合，構建合理的時變可靠度求解模型，提高了結構可靠度求解精度及合理性。

附圖說明

圖1是本發明針對層合板結構考慮時變效應的非概率可靠性求解方法流程圖；

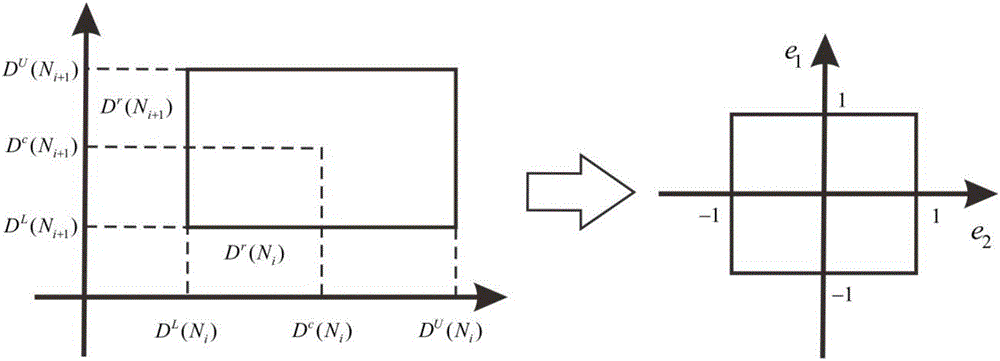
圖2是本發明的區間過程模型理論中標準化變換示意圖；

圖3是本發明定義的相關性函數所對應的幾何可行域示意圖；

圖4是本發明提出的首次穿越理論示意圖；

圖5是本發明提出的基于非概率理論求解穿越可能度指標示意圖；

圖6是本發明針對擬建的復合材料層合板結構幾何模型示意圖。

具體實施方式

下面結合附圖以及具體實施方式進一步說明本發明。

如圖1所示，本發明提出了一種針對復合材料層合板的非概率時變可靠性優化方法，包括以下步驟：

(1)利用區間向量x∈x^I＝(σ,D_cr,A,B,C)合理表征貧信息、少數據條件下的結構不確定性，于是有：

其中，結構強度R可表示為區間變量，上標U代表參量的取值上界，上標L代表參量的取值下界，上標c代表中心值，上標r代表半徑，不確定性參數向量x可以表示為：

x＝[x^L,x^U]＝[x^c-x^r,x^c+x^r]

＝x^c+x^r[-1,1]

＝x^c+x^r×e

其中，e∈Ξ²，Ξ²定義為所有元素包含在[-1,1]內的2維向量集合，符號“×”定義為兩個向量各對應元素相乘的算子，乘積仍為維數為2的向量。

(2)根據層合板結構(如圖6)的材料屬性：外部載荷σ，初始損傷D₀，引入區間變量結合結構損傷演化模型建立含不確定信息的損傷演化模型顯式表達式。即：

其中，σ為外部載荷區間變量，A,B為由試驗測得的試驗參數，C為損傷指數，通過試驗數據獲得，D₀為結構初始損傷。

(3)基于第二步所推演的損傷演化方程，對于任意給定載荷循環次數N_i，結構損傷將被量化為一個區間D(N_i)，有限個離散的區間變量D(N₁),D(N₂),...,D(N_n)的可行范圍被界定在一個超立方體域內。

基于區間數學理論，分別定義出任意給定載荷循環次數N_i條件下中心值和半徑如下：

結合損傷演化方程和區間泰勒級數展開法，可以求得：

其中，

對于任意給定的不同載荷循環次數N_i和N_i+1，如圖2所示，借助標準化處理手段，并轉換工作坐標系至(e₁,e₂)，即：

D(N_i)∈[D(N_i)^L,D(N_i)^U]＝D(N_i)^c+D(N_i)^r×e₁

D(N_i+1)∈[D(N_i+1)^L,D(N_i+1)^U]＝D(N_i+1)^c+D(N_i+1)^r×e₂

從幾何角度不難發現，存在無數多個不同形狀的偏轉矩形域包含于標準方形域內，而這些矩形域形狀的改變與其對應的區間變量相關性具有映射關系(如圖3所示)。于是，定義自相關性函數Cov_D(N_i,N_i+1)和相關系數函數ρ_D(N_i,N_i+1)如下：

其中，d表示如圖3所示矩形域邊長的一半，和分別是標準區間變量e₁和e₂的方差是一個無量綱量，其大小代表了D(N_i)和D(N_i+1)的線性相關度。

(4)將首次穿越理論與所建立的損傷演化模型相結合，如圖4，提出針對復合材料層合板結構的非概率時變可靠度計算指標：

其中，N表示整個服役周期，Pos{·}表示事件發生的可能性度量，D(σ,A,B,C,D₀,N_i)表示經歷N_i次載荷循環后板結構的損傷擴展量。G(N_i)表示層合板結構的極限狀態函數，G(N_i)＞0代表結構安全，反之意味著當前裂紋長度已超過許用值，結構會發生失穩破壞。上式中時變可靠度R_set(N)的計算需借助時間離散化方法，并遍歷每一個微小載荷歷程增量內結構發生裂紋失穩破壞的可能性指標，于是有：

其中，P_f(N)表示失效度，Pos(0)＝Pos(D_cr＜D₀)表示結構在初始缺陷作用下即發生失效的可能度，ΔN_i＝N_i+1-N_i表示微小載荷歷程增量。r(N_i)表示矩形板結構在循環加載N_i次到N_i+1次之間發生穿越失效的可能性指標，具體表達如下：

穿越失效可能度r(N_i)的可根據非概率可靠度求解方法求得，如圖5，通過干涉域面積與總體可行域面積的比值來表示，則層合板的失效時變可能度為：

則層合板機構的非概率時變可靠度為：

其中，為N_i-ΔN與N_i之間離散時間段內，出現干涉的區域面積，為時間段內可行域面積。

綜上所述，本發明提出了一種針對復合材料層合板結構，考慮時變效應作用下的非概率可靠性求解方法。首先，根據層合板結構材料以及載荷等情況的具體特征，結合損傷演化過程建立結構損傷演化方程；其次，將區間變量等不確定信息引入損傷演化方程給出不確定損傷演化方程的顯示表達；最后，基于首次穿越方法考慮損傷演化過程中的時變效應，結合非概率可靠度理論建立非概率時變可靠性求解方法。

以上僅是本發明的具體步驟，對本發明的保護范圍不構成任何限制；其可擴展應用于結構多失效模式的可靠性求解領域，凡采用等同變換或者等效替換而形成的技術方案，均落在本發明權利保護范圍之內。本發明未詳細闡述部分屬于本領域技術人員的公知技術。