一種精密引潮力的計算及其影響因素分析方法與流程

本發明涉及一種精密引潮力的計算及其影響因素分析方法，屬測繪技術領域。

背景技術：

精密引潮力的計算是地球物理、空間科學、天文/測地學研究的基本理論問題。張捍衛(2004)根據彈性力學的基本理論，從地球的微小彈性運動方程出發，給出了引潮力的嚴格數學定義，拋棄了前人對引潮力定義所給定的所有假設條件，回避了引潮力不同定義容易引起的歧義性。Hartmann&Wenzel(1995a,1995b)、Kudryavtsev(2004)基于引潮位理論公式和天體歷表，將月球、太陽、近地行星的引潮位分別展開至6階、3階、2階，計算得到引潮位及引潮力的時間序列。地球扁率對引潮力的計算存在影響，郗欽文(1999)和張捍衛(2010)分別指出，地球扁率對引潮力的影響不超過5×10^-11ms^-2(10^-11ms^-2＝1nGal)，這在高精度的潮汐分析、引潮力計算中是必須要考慮的。其實Bartels早在1957年就曾指出這一問題，隨后Wilhelm(1983)和Dahlen(1993)給出了相關的計算公式，Hartmann&Wenzel(1995a,1995b)在此基礎上，通過對公式中參數的數量級估計，表明當引潮力計算截斷閾值為0.001×10^-11ms^-2時，需要考慮地球扁率對月球和太陽引潮力的影響，對其它行星的影響則不需考慮。通常情況下，引潮力被認為是引潮位的徑向梯度值，而重力儀的測量數據是基于鉛垂線方向，因此需將徑向元素轉換為鉛垂線法向的元素，Wenzel(1974)指出此處可忽略垂線偏差的影響，只需將基于球面的徑向元素轉換為基于橢球面的法向元素即可。

在引潮力的計算過程中，天球參考系轉換、勒讓德函數計算是兩個核心工作，在以往的計算中(Hartmann&Wenzel,1995a,1995b；Roosbeek,1996；Kudryavtsev,2004)，對于前者采用經典的基于春分點的歲差章動轉換，對于后者采用手工推導出各階次的具體表達式；這種做法存在兩個不足：一是缺乏檢核條件，無法快速確定計算過程與結果的準確性；二是勒讓德函數表達式推導的難度隨著階次升高將會倍增，從而嚴重影響了引潮力數據計算準確性和可靠性，同時也導致計算過程相對復雜，不利于引潮力計算方法的推廣和掌握，同時，傳統的引潮力計算過程中，無法直接多的對引潮力計算結果產生干擾情況進行分析，從而進一步增加了傳統方法計算引潮力數據誤差率，因此針對這一問題，迫切需要開發一種全新的精密引潮力的計算方法，以滿足實際工作的需要。

技術實現要素：

本發明的目的是要提供一種精密引潮力的計算及其影響因素分析方法。

為達到上述目的，本發明是按照以下技術方案實施的：

一種精密引潮力的計算及其影響因素分析方法，其特征在于，所述的精密引潮力的計算及其影響因素分析方法包括如下步驟：

第一步，建立天體對地球上測站點的引潮位計算函數模型，根據待計算天體位置、觀測點所在地球位置參數為基礎，構建天體對地球上測站點的引潮位計算函數模型為：

其中，GM_J為萬有引力常數與天體J的質量之積；

R_J、r分別表示天體、測站點的地心距；

Z_J為天體與測站之間的地心天頂距，

P_n(x)為n階勒讓德函數；

第二步，天球參考系轉換，首先基于美國噴氣推進實驗室發布的DE歷表進行天體坐標計算工作，以地球為中心星、各天體為目標星計算得到天體坐標，該天體坐標是天體在GCRS坐標，然后并將天體在GCRS中的坐標轉換為ITRS中的坐標，在進行GCRS坐標轉換為ITRS中的坐標時，首先分別構建基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型，最后根據IERS規范中的GCRS坐標轉換為ITRS坐標的轉換參數及計算模型，分別引入到基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型中，并分別按照基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型進行數據運算，并將基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型計算的結果進行比對，且當基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型計算結果一致，則證明數據運算正確，從而進行下一步操作，當基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型計算結果不一致時，則證明數據運算不正確；

第三步，勒讓德函數及其導數運算，第一步構建的建天體對地球上測站點的引潮位計算函數模型中勒讓德函數P_n(x)，結合地心緯度參數，建立勒讓德函數P_n(sinθ)的遞推運算函數：

其中：θ為地心緯度，θ∈[-90°,90°](即對于天體θ＝δ、對于測站

n≥2；

同時基于勒讓德函數P_n(sinθ)，構建勒讓德函數P_n(sinθ)對sinθ的一階導數以及對θ的一階導數

的遞推公式為：

其中和在數據運算時均采用標準向前列遞推算法，其運算公式為：

其中n≥2且n>m；

m≥2；

n>m；

m≥0；

并由此得到：

則遞推初值為：

第四步，天體對地球上測站點的引潮力計算，首先基于測站點在ITRS中的地心經度、地心緯度得勒讓德函數P_n(x)的等價變形式，由球面三角學中邊的余弦公式得：

則存在以下關系式

其中為n階m次完全規格化締合勒讓德函數；

然后將勒讓德函數P_n(x)的變形式引入到天體對地球上測站點的引潮位計算函數模型中，并得到天體對地球上測站點的引潮位計算函數模型等價變形式：

其中a為地球參考橢球長半徑；

然后根據地球扁率對引潮位的影響計算函數：

其中J_2⊕為地球重力場二階帶球諧系數；

最后將地球上測站點的引潮位計算函數模型等價變形式得到的V^<1>值和然后根據地球扁率對引潮位的影響計算函數得到的V^<2>值求和，以得到天體對測站點總的引力值，其具體表達式為：

則引潮位的梯度值為：

其中：g_r,S、g_λ,S、分別表示測站點在球坐標系下的徑向引潮位徑向重力固體潮、徑向經度固體潮、徑向緯度固體潮；

第五步，天體對測站點總的引力值驗算，天體對測站點總的引力值驗算檢核計算公式：

此時記為測站點處的大地緯度B與球心緯度之差，則測站點在橢球坐標系下的引潮力g_r,E、法向經度固體潮g_L,E、法向緯度固體潮g_B,E驗算檢核計算公式為：

第六步，數據計算與分析，在進行精密引潮力的計算時，首先需要進行各天體展開階次及天體取舍，確定運算參數，然后在計算過程中分別對天體坐標轉換對計算結果影響、地球扁率對引潮位對計算結果影響、歲差章動模型更新及春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型運算對計算結果影響、徑向法向轉換對計算結果影響、參考框架偏差對計算結果影響、計算過程中地球時轉換對計算結果影響、極移對計算結果影響及歷表更新對計算結果影響進行驗證即可。

進一步的，所選擇的第二步中進行基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型進行數據計算時，均涉及到了ERA的計算，ERA的計算公式為：ERA(T_u)＝2π(0.7790572732640+1.00273781191135448T_u)；

其中T_u是從J2000.0起算的儒略日數，時間系統為UT1，這就涉及到TT與UT1之間的轉換，記二者的差值為ΔT＝TT-UT1，ΔT是基于最小二乘法擬合得到一組六次多項式，其具體表達式為：

進一步的，所述基于春分點的歲差章動轉換函數模型為：[ITRS]＝W(t)·R_eqx(t)·Q_eqx(t)·[GCRS]；

t為從J2000.0起算的TT儒略世紀數(以下相同)，[ITRS]、[GCRS]分別表示相應參考系中的三維直角坐標，Q_eqx(t)、R_eqx(t)、W(t)分別稱為框架偏差-歲差-章動矩陣、地球自轉矩陣、極移矩陣；

其中框架偏差-歲差-章動矩陣、地球自轉矩陣、極移矩陣表達式為：

B為參考框架偏差矩陣(簡稱框架偏差)，P為歲差矩陣，N為章動矩陣，它們的計算公式分別為：

ξ₀、η₀表示CIP在GCRS中J2000.0時刻的天極偏差，dα₀為瞬時平春分點的赤經偏差值；ψ_A、ω_A為基本赤道歲差參數，χ_A為黃道歲差導出量，ε_A為瞬時黃赤交角；Δψ為黃經章動，Δε為交角章動。

進一步的，所述基于CIO的無旋轉原點轉換函數模型為：[ITRS]＝W(t)·R_CIO(t)·Q_CIO(t)·[GCRS]；

Q_CIO(t)、R_CIO(t)也分別稱為框架偏差-歲差-章動矩陣、地球自轉矩陣；

Q_CIO(t)、R_CIO(t)的計算模型分別為：

R_CIO(t)＝R₃(ERA)；

其中：s為CIO定位角，表示CIO在CIP赤道上的位置，ERA為地球自轉角。

本發明一方面數據計算過程簡便。數據運算過程通用性強，便于對數據計算方法的掌握和交流，另一方面有效的克服了傳統引潮力計算過程中缺乏檢核條件，無法快速確定計算過程與結果的準確性和勒讓德函數表達式推導的難度隨著階次升高將會倍增的弊端，于此同時也便于對引潮力計算過程中易出現的干擾因素進行分析排除，從而極大的提高了引潮力計算工作的準確性和可靠性。

附圖說明

下面結合附圖和具體實施方式來詳細說明本發明

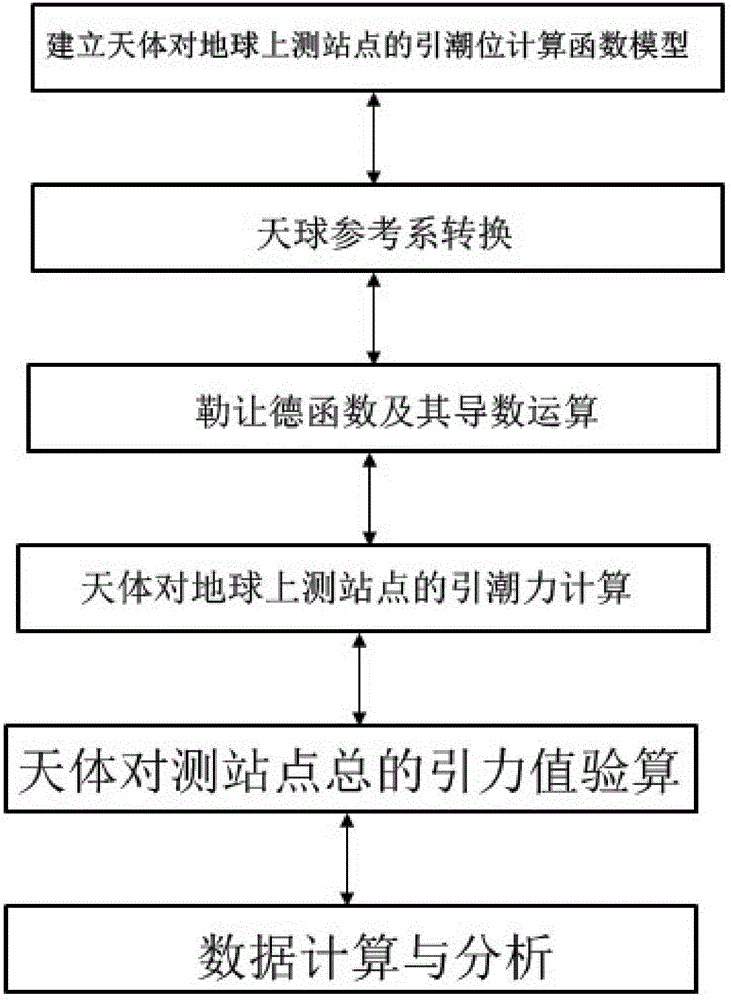
圖1：為本發明方法流程圖；

圖2：為天體、測站在地心天球中的位置示意圖。

具體實施方式

為使本發明實現的技術手段、創作特征、達成目的與功效易于明白了解，下面結合具體實施方式，進一步闡述本發明。

如圖1和2所示，一種精密引潮力的計算及其影響因素分析方法，其特征在于，所述的精密引潮力的計算及其影響因素分析方法包括如下步驟：

第一步，建立天體對地球上測站點的引潮位計算函數模型，根據待計算天體位置、觀測點所在地球位置參數為基礎，構建天體對地球上測站點的引潮位計算函數模型為：

其中，GM_J為萬有引力常數與天體J的質量之積；

R_J、r分別表示天體、測站點的地心距；

Z_J為天體與測站之間的地心天頂距，

P_n(x)為n階勒讓德函數；

第二步，天球參考系轉換，首先基于美國噴氣推進實驗室發布的DE歷表進行天體坐標計算工作，以地球為中心星、各天體為目標星計算得到天體坐標，該天體坐標是天體在GCRS坐標，然后并將天體在GCRS中的坐標轉換為ITRS中的坐標，在進行GCRS坐標轉換為ITRS中的坐標時，首先分別構建基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型，最后根據IERS規范中的GCRS坐標天體坐標轉換為ITRS坐標的轉換參數及計算模型，分別引入到基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型中，并分別按照基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型進行數據運算，并將基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型計算的結果進行比對，且當基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型計算結果一致，則證明數據運算正確，從而進行下一步操作，當基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型計算結果不一致時，則證明數據運算不正確；

第三步，勒讓德函數及其導數運算，第一步構建的建天體對地球上測站點的引潮位計算函數模型中勒讓德函數P_n(x)，結合地心緯度參數，建立勒讓德函數P_n(sinθ)的遞推運算函數：

其中：θ為地心緯度，θ∈[-90°,90°](即對于天體θ＝δ、對于測站

n≥2；

同時基于勒讓德函數P_n(sinθ)，構建勒讓德函數P_n(sinθ)對sinθ的一階導數以及對θ的一階導數

的遞推公式為：

其中和在數據運算時均采用標準向前列遞推算法，其運算公式為：

其中n≥2且n>m；

m≥2；

n>m；

m≥0；

并由此得到：

則遞推初值為：

第四步，天體對地球上測站點的引潮力計算，首先基于測站點在ITRS中的地心經度、地心緯度得勒讓德函數P_n(x)的等價變形式，由球面三角學中邊的余弦公式得：

則存在以下關系式

其中為n階m次完全規格化締合勒讓德函數；

然后將勒讓德函數P_n(x)的變形式引入到天體對地球上測站點的引潮位計算函數模型中，并得到天體對地球上測站點的引潮位計算函數模型等價變形式：

其中a為地球參考橢球長半徑；

然后根據地球扁率對引潮位的影響計算函數：

其中J_2⊕為地球重力場二階帶球諧系數；

最后將地球上測站點的引潮位計算函數模型等價變形式得到的V^<1>值和然后根據地球扁率對引潮位的影響計算函數得到的V^<2>值求和，以得到天體對測站點總的引力值，其具體表達式為：

則引潮位的梯度值為：

其中：g_r,S、g_λ,S、分別表示測站點在球坐標系下的徑向引潮位徑向重力固體潮、徑向經度固體潮、徑向緯度固體潮；

第五步，天體對測站點總的引力值驗算，天體對測站點總的引力值驗算檢核計算公式：

此時記為測站點處的大地緯度B與球心緯度之差，則測站點在橢球坐標系下的引潮力g_r,E、法向經度固體潮g_L,E、法向緯度固體潮g_B,E驗算檢核計算公式為：

第六步，數據計算與分析，在進行精密引潮力的計算時，首先需要進行各天體展開階次及天體取舍，確定運算參數，然后在計算過程中分別對天體坐標轉換對計算結果影響、地球扁率對引潮位對計算結果影響、歲差章動模型更新及春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型運算對計算結果影響、徑向法向轉換對計算結果影響、參考框架偏差對計算結果影響、計算過程中地球時轉換對計算結果影響、極移對計算結果影響及歷表更新對計算結果影響進行驗證即可。

本實施例中，所選擇的第二步中進行基于春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型進行數據計算時，均涉及到了ERA的計算，ERA的計算公式為：ERA(T_u)＝2π(0.7790572732640+1.00273781191135448T_u)；

其中T_u是從J2000.0起算的儒略日數，時間系統為UT1，這就涉及到TT與UT1之間的轉換，記二者的差值為ΔT＝TT-UT1，ΔT是基于最小二乘法擬合得到一組六次多項式，其具體表達式為：

本實施例中，所述基于春分點的歲差章動轉換函數模型為：[ITRS]＝W(t)·R_eqx(t)·Q_eqx(t)·[GCRS]；

t為從J2000.0起算的TT儒略世紀數(以下相同)，[ITRS]、[GCRS]分別表示相應參考系中的三維直角坐標，Q_eqx(t)、R_eqx(t)、W(t)分別稱為框架偏差-歲差-章動矩陣、地球自轉矩陣、極移矩陣；

其中框架偏差-歲差-章動矩陣、地球自轉矩陣、極移矩陣表達式為：

B為參考框架偏差矩陣(簡稱框架偏差)，P為歲差矩陣，N為章動矩陣，它們的計算公式分別為：

ξ₀、η₀表示CIP在GCRS中J2000.0時刻的天極偏差，dα₀為瞬時平春分點的赤經偏差值；ψ_A、ω_A為基本赤道歲差參數，χ_A為黃道歲差導出量，ε_A為瞬時黃赤交角；△ψ為黃經章動，△ε為交角章動。

本實施例中，所述基于CIO的無旋轉原點轉換函數模型為：[ITRS]＝W(t)·R_CIO(t)·Q_CIO(t)·[GCRS]；

Q_CIO(t)、R_CIO(t)也分別稱為框架偏差-歲差-章動矩陣、地球自轉矩陣；

Q_CIO(t)、R_CIO(t)的計算模型分別為：

R_CIO(t)＝R₃(ERA)；

其中：s為CIO定位角，表示CIO在CIP赤道上的位置，ERA為地球自轉角。

本實施例中，第六步中判斷天體坐標轉換對計算結果影響時，在進行精密引潮力的計算工作之前，首先需要確定參與計算的天體及其展開階數，基于現階段重力儀測量精度水平，并兼顧重力儀未來的發展，以|g_r,S,J|≥0.001×10^-11ms^-2(0.001nGal)為計算截斷閾值，由于：

取r_max＝a，對于x∈[-1,1]，|P_n(x)|≤1，對于天體J而言，其第n階參與計算的條件為：

基于DE431歷表，計算得到1000AD～3000AD共計2000年內時間間隔為1天的各天體地心距序列，統計得到最小地心距min(R_J)，并根據DE431歷表中給出的GM_J數值，即可得到各天體在各階次引潮力最大值

在計算過程中，理論上引潮力的計算至0.001×10^-11ms^-2即可，但為了分析各類影響因素對引潮力計算影響的具體量值，實際計算至0.000001×10^-11ms^-2即可。

本實施例中，第六步中判斷天體坐標轉換對計算結果影響時，為確保計算過程與結果的準確性，對天體坐標轉換，分別采用基于春分點的歲差章動轉換、基于CIO的無旋轉原點轉換兩種方法，轉換模型中的參數又分別基于IERS 2003、2010規范推薦的四組參數計算模型；對引潮力計算公式，分別采用基于勒讓德函數及其導數遞推算法、完全規格化締合勒讓德函數及其導數遞推算法兩種數學模型得到的第四步的天體對地球上測站點的引潮力計算式。

在下列各項影響因素計算過程中，均采用第四步的天體對地球上測站點的引潮力計算式分別獨立計算得到V、g_r,S、g_λ,S、序列，然后由(8)式轉換為V、g_r,E、g_L,E、g_B,E序列。計算結果表明：對各個序列而言，兩組公式結果間的差值ΔV、Δg_r,E、Δg_L,E、Δg_B,E序列均為零，這就從勒讓德函數遞推計算方面確保了計算過程與計算結果的準確性。

在天體坐標轉換方面，計算結果表明：兩個規范中轉換參數模型間的差異、兩種坐標轉換方法間的差異對引潮力計算的影響非常微小，可完全忽略不計，這就從天體坐標轉換方面確保了計算過程與計算結果的準確性。

本實施例中，第六步中判斷地球扁率對引潮位對計算結果影響時，引潮位V^<1>是將地球作為均質球體得到的，而真實的地球則是一個兩級略扁的旋轉橢球體，因此地球扁率就對引潮位的計算帶來影響，因此需要計算得到由地球扁率而引起的各天體對測站引潮位與引潮力影響的具體數值，并由此得到由地球扁率引起的月球對測站引潮位與引潮力的影響分別在0.00013m²s^-2、1.890×10^-11ms^-2、1.994×10^-11ms^-2、1.909×10^-11ms^-2以內；由地球扁率引起的太陽對測站引潮位與引潮力的影響分別在0.00000011m²s^-2、0.002×10^-11ms^-2、0.002×10^-11ms^-2、0.002×10^-11ms^-2以內；對其它天體的影響均為零，因此，在精密引潮力的計算過程中，只需考慮地球扁率對月球、太陽的影響即可。

本實施例中，第六步中判斷歲差章動模型更新及春分點的歲差章動轉換函數模型和基于CIO的無旋轉原點轉換函數模型運算對計算結果時，針對兩種坐標轉換方法，IERS 2003、2010規范分別推薦了兩套4組不同的轉換參數，為明確歲差章動模型更新、不同坐標轉換方法間的差異對引潮力計算的影響，分別基于不同的歲差章動模型和坐標轉換方法，計算得到相應序列，并分別設為基于2010A、2010B、2003A、2003B四種坐標轉換模型，計算得到V、g_r,E、g_L,E、g_B,E四組序列值，差值序列即反映了歲差章動模型更新、不同坐標轉換方法間差異對引潮位與引潮力計算的影響，并得到歲差章動模型更新2010A-2003A、2010B-2003B對引潮位與引潮力的影響分別在2×10^-8m²s^-2、0.00061×10^-11ms^-2、0.00047×10^-11ms^-2、0.00040×10^-11ms^-2以內；不同坐標轉換方法2010A-2010B、2003A-2003B的影響量值分別在2×10^-10m²s^-2、0.000005×10^-11ms^-2、0.000004×10^-11ms^-2、0.000003×10^-11ms^-2以內；

這說明歲差章動模型更新、兩種坐標轉換方法間的差異對引潮位與引潮力計算的影響甚微，實際計算時可完全忽略不計。在引潮位與引潮力的計算中，可采用任意歲差章動模型及坐標轉換方法。

本實施例中，第六步中判斷徑向法向轉換對計算結果影響時，計算得到的g_r,S、g_λ,S、是徑向梯度結果，需根據將其轉換為法向結果。若忽略徑向到法向的轉換，就對引潮位與引潮力的計算帶來影響。

若忽略徑向到法向的轉換，對V和g_L,E的數值沒有影響，對g_r,E、g_B,E影響的最大值分別達到476×10^-11ms^-2、500×10^-11ms^-2，該影響量值遠遠超出允許的精度范圍，即計算結果錯誤。因此，在引潮力計算中，一定不能忽略將徑向結果轉換為法向結果，否則結果錯誤。

本實施例中，第六步中判斷數據運算參考數據源框架對計算結果影響時，參考框架偏差是由于在標準歷元J2000.0時刻歲差章動模型給出的天極、分點與GCRS的天極、經度零點不重合造成的。IERS 2003、2010規范中考慮了參考框架偏差對天體坐標轉換的影響，但在IERS 1996規范中并沒有考慮該影響。

以2010A模型為例，計算了在基于春分點的歲差章動轉換過程中，當忽略參考框架偏差時，對引潮位與引潮力的影響量值分別在1×10^-6m²s^-2、0.032×10^-11ms^-2、0.032×10^-11ms^-2、0.021×10^-11ms^-2以內。

本實施例中，第六步中判斷計算過程中地球時轉換對計算結果影響時，在計算ERA時，如果誤將時間尺度用作TT，即忽略了地球時與世界時的差值ΔT，就會對引潮位與引潮力計算結果帶來影響。

如果忽略地球時與世界時間的轉換，對引潮位及引潮力的影響量值分別達到0.03m²s^-2、916×10^-11ms^-2、1144×10^-11ms^-2、696×10^-11ms^-2，該影響量值遠遠超出允許的精度范圍，即計算結果錯誤。

因此，在引潮力計算中，一定不能忽略地球時與世界時轉換的影響，否則結果錯誤。

本實施例中，第六步中判斷極移對計算結果影響時，由于極移量x_p、y_p的具體數值目前無法準確預測，只能根據EOP 08C04模型中已發布的相關數據進行計算。中國天文年歷在進行天體坐標轉換時，并沒有考慮極移的影響，實際上是將天體坐標轉換至TIRS。由于在兩種坐標轉換方法中，極移影響與歲差章動模型無關，因此極移對坐標轉換的影響量對兩種坐標轉換方法、兩個規范而言均是相同的。本文計算了當忽略極移時，對引潮位與引潮力的影響量值分別在2×10^-5m²s^-2、0.586×10^-11ms^-2、0.543×10^-11ms^-2、0.341×10^-11ms^-2以內。

本實施例中，第六步中判斷歷表更新對計算結果影響時，隨著天體測量理論與技術的進步，尤其是精度更高的天體測量數據的積累，JPL不斷的對DE歷表進行更新，發布了一系列版本的歷表，其中比較著名的有DE200、DE403、DE405、DE406、DE413、DE421、DE423等，目前最新的是2014年發布的DE432歷表。在IERS 2003、2010規范中，分別將DE405、DE421歷表作為ICRS的動力學實現。

在后續的引潮位頻譜法展開研究中，采用DE431歷表，其覆蓋時間范圍為30000年(13200BC～17191AD)。為明確歷表更新對引潮力的影響，分別基于DE405、DE421、DE431歷表，計算了相應的序列，并統計出各序列間的差異。

歷表更新對引潮位與引潮力的影響量值分別在4×10^-7m²s^-2、0.012×10^-11ms^-2、0.013×10^-11ms^-2、0.013×10^-11ms^-2以內。

歷表更新對引潮力的影響有兩方面原因：一是由于歷表自身精度的提高；二是不同歷表采用的天文常數系統不同，在DE405、421、431三個歷表中，各天體GM值以及定義距離的AU(Astronomical Unit，天文單位)都是不同的。

本發明一方面數據計算過程簡便。數據運算過程通用性強，便于對數據計算方法的掌握和交流，另一方面有效的克服了傳統引潮力計算過程中缺乏檢核條件，無法快速確定計算過程與結果的準確性和勒讓德函數表達式推導的難度隨著階次升高將會倍增的弊端，于此同時也便于對引潮力計算過程中易出現的干擾因素進行分析排除，從而極大的提高了引潮力計算工作的準確性和可靠性。

本行業的技術人員應該了解，本發明不受上述實施例的限制，上述實施例和說明書中描述的只是說明本發明的原理，在不脫離本發明精神和范圍的前提下，本發明還會有各種變化和改進，這些變化和改進都落入要求保護的本發明范圍內。本發明要求保護范圍由所附的權利要求書及其等效物界定。