增強橋梁健康監測結構響應和溫度數據相關性收斂的方法與流程

本發明屬于橋梁健康監測數據相關性分析研究領域，涉及一種溫度作用下橋梁結構響應相關性分析方法。

背景技術：

橋梁健康監測系統數據相關性分析是橋梁結構分析研究的重要內容，環境荷載是橋梁結構主要荷載之一。溫度荷載特性分析是橋梁結構設計、施工、運營的重要工作。溫度作用下的結構響應與其相關性分析，能夠得到響應在溫度荷載作用下的內在規律，對橋梁結構的評估和預警有著重要的意義。環境荷載具有很強的規律性，在天氣良好的情況下，一般呈現‘類正弦’型變化趨勢，諸多結構幾何線性變化監測數據(如撓度、位移、傾角等)在溫度作用下有著較為明顯的相關關系。

近年來隨著橋梁健康監測技術的發展，健康監測系統被廣泛應用與橋梁結構，因而可以直接獲取橋梁在實測荷載作用下的結構響應數據從而有效避免傳統的理論推導、有限元模擬和風洞試驗存在初始參數賦值偏差、初始邊界條件設定偏差以及次要影響因素的不恰當忽略的問題。然而目前，國內外對結構響應和溫度相關性影響因素以及如何消減干擾獲得更加收斂相關性關系的研究工作不足。溫度作用下結構構件響應的真實相關性規律仍然未知，迫切需要一種能夠消除或者減小對監測數據間相關性分許干擾的有效方法。

技術實現要素：

發明目的：本發明提供一種可以有效消除監測數據時滯效應和減小數據間頻率差異對相關性的影響，最終得到等效溫度和結構響應間良好相關關系，更加快捷有效的增強橋梁健康監測結構響應和溫度數據相關性收斂的方法。

技術方案：本發明的增強橋梁健康監測結構響應和溫度數據相關性收斂的方法，包括以下步驟：

第一步：獲取健康監測系統溫度數據及其在時間上對應的結構響應數據，包括結構響應數據時間序列f_sr，溫度數據時間序列x_{ij i＝1,2,...,m,j＝1,2,...n}，其中，i表示傳感器編號，j表示數據長度，m為時程數據的條數，n為每條時程數據的個數；

第二步：使用best-smooth數據波動性消減算法分別對健康監測系統溫度數據f_temp和對應的結構響應數據f_sr進行光滑處理，得到光滑處理后的溫度數據f_{temp，smooth}和結構響應數據f_sr，smooth；

第三步：利用傅里葉級數消除時滯效應并減小頻率差異對監測數據間相關性關系的影響，具體流程為：

(1)首先使用傅里葉級數對第二步中得到的數據f_sr，smooth，f_{temp，smooth}進行頻率分解，得到數據信號頻率成分參量，具體流程為：

1)根據下式計算初始參量u₁和臨時參量u₂：

i＝2p,2p-1,2n-2,...2,1

其中，f_i代表數據在λ_i處的值，λ_i為數據位置，k是正弦信號階數；

2)根據下式計算傅里葉因子的余弦系數a_k和正弦系數b_k：

其中，f₁為數值信號中第一個數據的值；

3)根據下式得到各階頻率對應的相位φ_k：

其中，a₀,a₁,a₂,...,a_k分別是f(λ)傅里葉因子的余弦系數，b₁,b₂,…,b_k分別是f(λ)的傅里葉因子的正弦系數，f(λ)為光滑數據信號傅里葉級數逼近表達式，信號各階振幅為φ_k＝arctan(a_k/b_k)，k＝1,2,3,...；

(2)求解光滑處理后的結構響應數據f_sr，smooth和光滑處理后的溫度數據f_{temp，smooth}間各個相同頻率下的相位差△φ_i，具體流程為：

1)根據傅里葉級數逼近表達式分別計算結構響應數據f_sr，smooth的相位φ_sr，k，溫度數據f_{temp，smooth}的相位φ_temp，k：

結構響應數據f_sr，smooth的傅里葉級數逼近表達式為：

溫度數據f_{temp，smooth}的傅里葉級數逼近表達式為：

2)根據下式計算相位差△φ_i：

△φ_i＝φ_temp,i-φ_sr,i,i＝1,2,3,...,k

其中，φ_temp,i為i階溫度數據相位，φ_sr,i為i階結構響應數據相位；

(3)確定傅里葉級數展開的最小階數k_min，并計算消除時滯效應后的結構響應數據f_{sr，deltime-leg}，具體流程為：

1)計算結構數據的傅里葉展開值f_fourier和數據光滑處理值f_smooth之間的均方根由RMSE<0.001確定結構響應數據的傅里葉級數展開最小階數k_min；

2)將結構響應數據傅里葉級數中的各個頻率成分的相位轉化為溫度信號相位，即平移△φ_i相位，然后通過下式對平移△φ_i相位后的結構響應數據進行處理，得到消除時滯后的結構響應數據f_{sr，deltime-leg}：

其中，a_sr,0為結構響應數據的傅里葉因子的余弦系數，c_sr,k是消除時滯效應后結構響應數據傅里葉展開式中k階正弦信號的振幅；

第四步：計算等效溫度數據T并計算消除時滯效應后的結構響應數據和溫度數據間的相關性系數γ，具體流程為：

(1)采用多元線性回歸法獲得消除時滯后結構響應數據f_{sr，deltime-leg}和m條原溫度時程監測數據{x₁,x₂,x₃,...,x_m}間最佳線性擬合參數b₀,b₁,b₂,...,b_m，并根據下式計算消除時滯后結構響應數據f_{sr，deltime-leg}的最佳擬合值f′_{sr，deltime-leg}：

f′_{sr，deltime-leg}＝b₀+b₁x₁+b₂x₂+…+b_mx_m；

(2)由下式計算得到等效溫度數據T：

其中，x_m,j為第m條溫度數據中第j個數據，b_m為多元線性回歸參數；

(3)由下式計算消除時滯效應后的結構響應數據和溫度數據間的相關性系數γ：

其中，為消除時滯效應后的結構響應數據的均值，為等效溫度數據均值。

進一步的，本發明方法中，第二步的具體流程為：

1)在健康監測時程數據f，即結構響應數據f_sr和溫度數據f_temp上加上長度為J(λ)的窗口；

2)將所述窗口在時程數據上按照長度J(λ)由前向后移動，同時采用高斯擬合函數S(λ)對窗口內J(λ)個數據進行三階以上的高斯擬合，然后通過下式確定最佳的長度函數J_best(λ)和每個區段最佳高斯擬合函數S_best(λ)：

{J_best(λ)，S_best(λ)}＝min{e²(S,J)＝E(λ,f)[f-S(λ/J(λ))]²}

其中，e²(S,J)為誤差期望，J(λ)為窗口長度，S(λ)為窗口內數據高斯擬合函數，λ為時程數據的位置，由{J_best(λ)，S_best(λ)}得到數據光滑值f_smooth，即結構響應數據的光滑值f_sr，smooth和溫度數據的光滑值f_{temp，smooth}。

進一步的，本發明方法中，第二步的步驟1)中，長度J(λ)的初始值設定為待光滑數據長度的十分之一。

有益效果：本發明與現有技術相比，具有以下優點：

1、該方法首次提出消除結構時滯效應的方法，并合理解釋數據間相關性呈現橢圓型分布的原因，同時首次應用多種數值信號處理方法消除或者較小時滯效應和頻率差對數據間相關性的影響，從而得到健康監測系統數據間更加收斂的相關性性質。

2、目前溫度作用下的結構響應數據間相關性分析缺乏可靠的理論依據和有效的分析方法，致使很多結構響應數據與溫度間找不出有規律可循的相關性關系。本發明基于傅里葉級數原理、多元線性回歸理論，利用best-smooth、MLR等算法，獲得了結構線性響應數據與溫度數據間更加收斂的相關性關系，因此具有很強的工程和科研應用前景。

3、本發明的主要功能已經程序化實現，操作簡便，具有很強的實用性。根據實際監測數據，該方法可以有效消除監測數據時滯效應和減小數據間頻率差異對相關性的影響，最終得到等效溫度和結構響應間良好的相關關系。因此，可以廣泛應用與健康監測系統數據間的相關性分析。

附圖說明

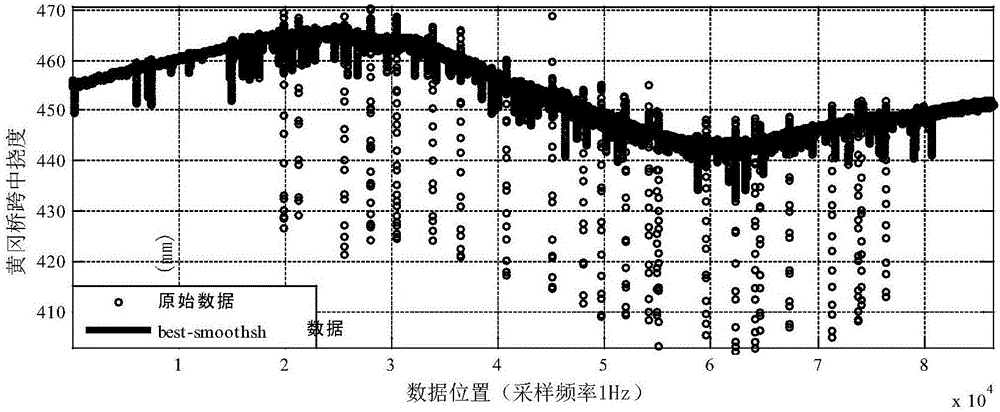
圖1為本發明實施例橋梁跨中撓度光滑處理圖；

圖2為本發明實施例監測數據光滑處理前后相關性對比圖；

圖3為本發明實施例監測數據消除時滯前后相關性對比圖；

圖4為本發明實施例撓度和等效溫度數據線性回歸圖。

具體實施方式

下面將參照附圖，對本發明的技術方案進行詳細的說明。

本發明的增強橋梁健康監測系統結構響應與溫度相關性收斂的方法，包括以下步驟：

第一步：獲取健康監測系統溫度數據及其在時間上對應的結構響應數據；

結構響應數據時間序列采用f_sr表示，溫度數據時間序列采用x_{ij i＝1,2,...,m,j＝1,2,...n}表示。其中，i表示傳感器編號，j表示數據長度。

第二步：使用best-smooth數據波動性消減算法對監測數據光滑處理，得到f_sr，smooth，f_{temp，smooth}。

第三步：利用傅里葉級數消除時滯效應并減小頻率差異對監測數據間相關性關系的影響，具體流程為：

(1)首先使用傅里葉級數對第二步中得到的數據f_sr，smooth，f_{temp，smooth}進行頻率分解，得到數據信號頻率成分參量，具體流程為：

1)根據下式計算初始參量u₁和臨時參量u₂：

i＝2p,2p-1,2n-2,...2,1

其中，f_i代表數據在λ_i處的值，λ_i為數據位置，k是正弦信號階數；

2)根據下式計算傅里葉因子的余弦系數a_k和正弦系數b_k：

其中，f₁為數值信號中第一個數據的值；

3)根據下式得到各階頻率對應的相位φ_k：

其中，a₀,a₁,a₂,...,a_k分別是f(λ)傅里葉因子的余弦系數，b₁,b₂,…,b_k分別是f(λ)的傅里葉因子的正弦系數，f(λ)為光滑數據信號傅里葉級數逼近表達式，信號各階振幅為φ_k＝arctan(a_k/b_k)，k＝1,2,3,...；

(2)求解光滑處理后的結構響應數據f_sr，smooth和光滑處理后的溫度數據f_{temp，smooth}間各個相同頻率下的相位差△φ_i，具體流程為：

1)根據傅里葉級數逼近表達式分別計算結構響應數據f_sr，smooth的相位φ_sr，k，溫度數據f_{temp，smooth}的相位φ_temp，k：

結構響應數據f_sr，smooth的傅里葉級數逼近表達式為：

溫度數據f_{temp，smooth}的傅里葉級數逼近表達式為：

2)根據下式計算相位差△φ_i：

△φ_i＝φ_temp,i-φ_sr,i,i＝1,2,3,...,k

其中，φ_temp,i為i階溫度數據相位，φ_sr,i為i階結構響應數據相位；

(3)確定傅里葉級數展開的最小階數k_min，以及計算消除時滯效應后的結構響應數據f_{sr，deltime-leg}：

1)計算結構數據的傅里葉展開值f_fourier和數據光滑處理值f_smooth之間的均方根由RMSE<0.001確定結構響應數據的傅里葉級數展開最小階數k_min；

2)將結構響應數據傅里葉級數中的各個頻率成分的相位轉化為溫度信號相位，即平移△φ_i相位，然后通過下式對平移△φ_i相位后的結構響應數據進行處理，得到消除時滯后的結構響應數據f_{sr，deltime-leg}：

其中，a_sr,0為結構響應數據的傅里葉因子的余弦系數，c_sr,k是消除時滯效應后結構響應數據傅里葉展開式中k階正弦信號的振幅；

第四步：計算等效溫度數據T并計算消除時滯效應后的結構響應數據和溫度數據間的相關性系數γ。

(1)建立消除時滯效應結構響應數據f_{sr，deltime-leg}和原溫度監測數據的多元線性回歸模型：

消除時滯結構響應數據f_{sr，deltime-leg}對溫度變量{x₁,x₂,x₃,...,x_m}的m元線性回歸方程為：

其中的b₀,b₁,b₂,...,b_m為系數的最小二乘估計值，為多元線性方程回歸估計值。可以按照以下方程組求解。

其中：

i,k＝1,2,...,m；i≠k

(2)根據多元線性回歸參數b₀,b₁,b₂,...,b_m計算等效溫度并建立消除時滯后的結構響應數據f_{sr，deltime-leg}和等效溫度數據T的一元線性回歸方程并計算消除時滯效應后的結構響應數據和溫度數據間的相關性系數γ：

f′_sr＝a₀+a₁T(x_j),j＝1,2,3,...n

其中，x_m,j為第m條溫度數據中第j個數據，b_m為多元線性回歸參數，f′_sr為f_{sr，deltime-leg}和等效溫度T(x_j)之間的線性擬合值，a₀，a₁為線性擬合參數，為消除時滯效應后的結構響應數據的均值，為等效溫度數據均值。|γ|越大，表示相關性越顯著。

(1)黃岡公鐵兩用長江大橋全長4010.81m，其中，公鐵合建段全長2566.135m(含斜拉橋主橋1215m)，跨度布置為：11×32.7m+1.7m+(81+243+567+243+81)m+1.7m+(40+56+40)m+26×32.7m。黃岡公鐵兩用長江大橋主橋為雙塔雙索面鋼桁梁斜拉橋，橋塔基礎均采用了31根3m大直徑鉆孔灌注樁，高樁承臺基礎；橋塔采用H性混凝土結構，塔高193.5m(含臺座)；主橋鋼桁梁采用雙主桁N性桁架，為上寬下窄倒梯形新型截面形式，全橋鋼桁梁4.6萬噸；斜拉索為空間雙索面，采用平行鋼絲索，全橋共計152根，其中最大規格為PESC7-475，索長約296m，自重約47噸。

(1)基于步驟一對主梁跨中部位的撓度響應監測數據及對應的溫度數據采集，儀器采樣頻率均為1Hz。選取2015年8月16日至8月18日的跨中撓度和溫度監測數據分析；

(2)基于步驟二對步驟一中獲得的溫度和撓度數據光滑處理，如圖1，2所示。

(3)基于步驟三消除監測數據時滯效應，如圖3所示。健康監測撓度和溫度光滑數據傅里葉級數各階相位差見表1。

表1撓度和溫度監測數據傅里葉級數前15階頻率參數及其相位差

(4)基于步驟四計算等效溫度數據T并計算消除時滯效應后的結構響應數據和溫度數據間的相關性系數γ。

采用大橋跨中4個溫度傳感器和撓度傳感器監測數據，通過步驟二，三得到消除時滯后的撓度時間序列，按照步驟四得到最優回歸模型。

表2溫度和撓度監測數據多元線性回歸模型參數

計算等效溫度:

對等效溫度和消除時滯的結構撓度數據建立一元線性回歸關系，如圖4所示。并計算消除時滯效應后的結構響應數據和溫度數據間的相關性系數γ_deltime-leg＝0.876顯著大于原始結構響應數據和溫度數據間的相關性系數γ_deltime-leg＝0.412，驗證此方法快捷有效。

上述實施例僅是本發明的優選實施方式，應當指出：對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和等同替換，這些對本發明權利要求進行改進和等同替換后的技術方案，均落入本發明的保護范圍。