一種基于數據挖掘技術的氣動特性數據處理方法與流程

本發明涉及一種基于數據挖掘技術的氣動特性數據處理方法，適用于面對稱高速再入飛行器，屬于飛行器氣動設計領域。

背景技術：

在航天工程研制、運行的全過程中，都會產生大量數據。航天數據不僅具有一般大數據的特點，而且要求高可靠、高精度和更高的處理速度。目前氣動設計中的氣動特性分析大多還是依賴傳統的曲線分析，彈道、姿控等專業對氣動數據的使用也大多采用數據表和線性插值的方式，一方面需要根據數據格式專門編制程序處理數據，另一方面插值方法也會帶來基本數據和高階導數的誤差，對氣動特性分析的效率和使用準確度都造成了影響，需要用更高準確度且更易使用的氣動數據處理方法加以改進。

技術實現要素：

本發明解決的技術問題是：克服現有技術的不足，提供了一種基于數據挖掘技術的氣動特性數據處理方法，有效提高了氣動特性分析的效率和使用準確度。

本發明的技術解決方案是：一種基于數據挖掘技術的氣動特性數據處理方法，包括以下步驟：

(1)選取飛行器的樣本點數據，將其按狀態參數變量和氣動特性參數變量進行分類，其中狀態參數變量包括馬赫數Ma、攻角α、側滑角β、舵偏角δ_j、高度H、雷諾數Re、努森數Kn，氣動特性參數變量包括氣動力六分量，即氣動力分量(Cx,Cy,Cz)和氣動力矩分量(U,V,W)，每個狀態參數變量和一個氣動特性參數變量構成一個變量對；

(2)計算每個變量對的相關系數，記狀態參數變量為自變量，氣動特性參數變量為因變量，按相關系數從大到小的順序對自變量排序，選取前2/3的自變量；

(3)計算自變量對每個因變量影響的權重系數，按權重系數從大到小的順序對自變量排序，選取前2/3的自變量；

(4)取步驟(2)和步驟(3)選取自變量的并集作為建模自變量；

(5)通過離群點分析法剔除氣動力六分量明顯不合理的數據點，根據剩余數據點通過多元高次交互回歸建立氣動力數據模型；

(6)從樣本點數據集合中選取80％為訓練集，剩余的20％為測試集，根據訓練集中的數據，利用氣動力數據模型計算預測值，并與測試集比對，利用如下公式計算平均相對誤差MAPE：

其中pred_i為第i個樣本的預測值，true_i為第i個樣本在實際測試集中的值，N為樣本總數；

(7)如果MAPE小于等于5％，則氣動力數據模型達到要求，根據氣動力數據模型以及樣本點數據獲得飛行器設計空間的所有氣動特性數據，如果MAPE大于5％，則氣動力數據模型不符合要求，返回步驟(2)，在步驟(2)中補充選取拋棄自變量中前2/3的自變量，在步驟(3)中補充選取拋棄自變量中前2/3的自變量，直到MAPE小于等于5％。

所述步驟(2)中計算每個變量對相關系數的方法如下：

(2.1)為每對變量對中所有樣本點涉及的自變量編秩，為所有樣本點涉及的因變量編秩；

(2.2)利用公式計算每個變量對的相關系數ρ，其中d_k代表第k組變量對因變量和自變量的排行差，d_k＝因變量的秩次-自變量的秩次。

所述步驟(3)中計算自變量對每個因變量影響的權重系數的方法如下：

(3.1)設樣本點數據中第j個因變量的數值為n×1的向量y，自變量數值對應n×M的矩陣x，M為自變量個數；

(3.2)對矩陣x利用公式x＝pΔq'進行分解，其中矩陣p由xx'的特征向量組成，q由x'x的特征向量組成，Δ為對角線矩陣，對角線為矩陣x的特征值；

(3.3)利用公式W＝qp'y計算自變量對第j個因變量的影響權重W。

在步驟(6)中分五次選取不同的數據作為測試集，分別計算MAPE，如果五次的MAPE均小于等于5％，則氣動力數據模型合適，否則認為氣動力數據模型不合適。

當氣動力數據模型不合適時，通過步驟(2)和步驟(3)補充選取自變量后，在步驟(5)中采用更高次的回歸方法進行建模。

本發明與現有技術相比的優點在于：

(1)采用了數據挖掘中的相關分析法分析狀態參數變量和氣動特性參數變量之間的關聯關系，能夠基于大量數據以單幅圖顯示變量間的影響關系，相對傳統的曲線圖，可以快速直觀的展示出飛行器氣動特性隨各狀態參量的變化規律和氣動特性本身的三通道耦合規律，提高了氣動特性分析的效率。

(2)通過高次交互回歸方法，結合狀態參數影響權重分析方法，高效準確的給出氣動模型，利用該氣動力數據模型獲得的氣動數據精確度更高，避免了傳統的氣動數據庫線性插值以及高階導數缺失帶來的準確度下降問題，有效提高了氣動數據的使用準確度。

(3)通過氣動模型將氣動數據轉化為簡單的公式形式，各專業對氣動數據的使用無需再通過讀入龐大的數據表實現，明顯提升了氣動數據的分析和使用效率。

(4)通過計算狀態參數對氣動特性的相關系數和權重系數，可以明確各狀態參數在建模中的重要度，方便使用者根據模型精度要求進行建模參數選取；并且，通過五重交叉驗證和模型迭代修正，確保了氣動力數據模型的高精準度，獲得準確度可控的適用于工程設計的氣動模型。

附圖說明

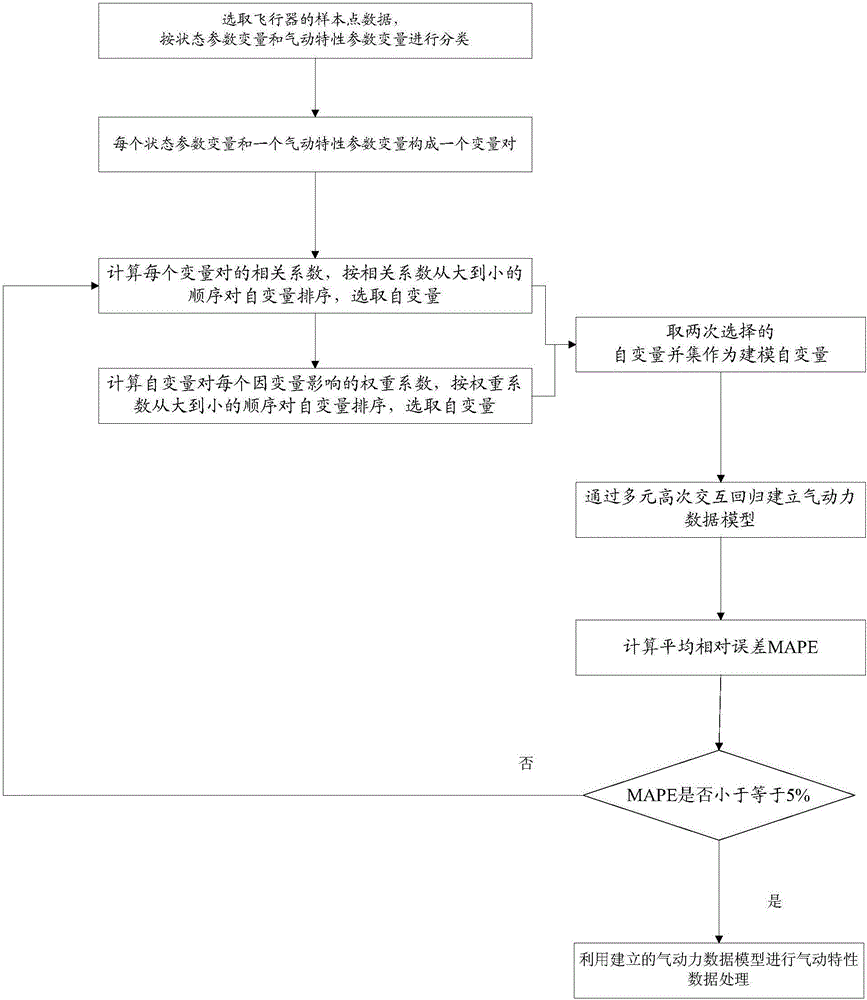
圖1為本發明方法流程圖；

圖2為本發明實施例飛行器示意圖；

圖3為氣動特性參數變量與狀態參數變量之間的相關性示意圖；

圖4為各個自變量對氣動力Cx的影響權重示意圖；

圖5為本發明方法與傳統差值方法得到的預測值與實際值的平均相對誤差對比圖。

具體實施方式

下面結合附圖和實施例對本發明做進一步說明。

一般飛行器研制過程中會產生大量的氣動數據，對氣動特性變化規律和影響因素的快速掌握對飛行器設計有著重要意義，鑒于傳統氣動數據處理方法對氣動特性分析的效率和使用準確度的影響，本發明考慮引入數據挖掘技術進行氣動特性變化規律方面的研究，并在掌握規律的基礎上進行氣動建模，提升氣動數據使用的精準度和效率。

在氣動特性參數與飛行狀態參數的相關性分析中，基于樣本點數據整理了氣動專業數據，按照自變量和因變量分為兩類，自變量主要指狀態參數，因變量主要指氣動特性參數。狀態參數有馬赫數、攻角、側滑角、舵偏角、高度、Re、Kn、氣動布局參數等；氣動特性參數主要指氣動力六分量、氣動不確定度等。根據提供的氣動數據，開展狀態參數和氣動特性參數之間規律的研究。

如圖1所示，本發明的具體步驟如下：

(1)選取飛行器的樣本點數據，將其按狀態參數變量和氣動特性參數變量進行分類，其中狀態參數變量包括馬赫數Ma、攻角α、側滑角β、舵偏角δ_j、高度H、雷諾數Re、努森數Kn；氣動特性參數變量包括氣動力六分量，即氣動力分量(Cx,Cy,Cz)和氣動力矩分量(U,V,W)，每個狀態參數變量和一個氣動特性參數變量構成一個變量對。

(2)計算每個變量對的相關系數，按相關系數從大到小的順序對自變量排序，選取前2/3的自變量，記狀態參數變量為自變量，氣動特性參數變量為因變量。

計算每個變量對相關系數的方法如下：

(2.1)為每對變量對中所有樣本點涉及的自變量編秩，為所有樣本點涉及的因變量編秩，數值相同的自變量秩次相同，數值相同的因變量秩次相同；例如，某變量對(x₁，y)中，x₁對應的樣本點為(1，1，3，5，7，11)，則其對應的秩次為(1，1，2，3，4，5)；y對應的樣本點為(0.1，0.3，0.3，0.2，0.4，0.6)，則其對應的秩次為(1，3，3，2，4，5)。

(2.2)利用公式

計算每個變量對的相關系數ρ，其中d_k代表第k組變量對樣本點因變量和自變量的排行差，d_k＝因變量的秩次-自變量的秩次，N為樣本總數。ρ的范圍在-1到1之間，當ρ為1，說明該變量對中兩個變量正相關。當ρ為-1，說明該變量對中兩個變量呈負相關。當ρ為0，說明該變量對中兩個變量不相關。利用-1到1之間的系數值，量化地表示出變量之間的相關關系，便于分析和比較。

(3)采用影響權重分析獲得各個變量間的相關程度，計算自變量對每個因變量影響的權重系數，按權重系數從大到小的順序對自變量排序，選取前2/3的自變量。

計算自變量對每個因變量影響的權重系數的方法如下：

(3.1)設樣本點數據中第j個因變量的數值為n×1的向量y，自變量數值對應n×M的矩陣x，M為自變量個數；

(3.2)對矩陣x利用公式

x＝pΔq' (2)

進行分解，其中矩陣p由xx'的特征向量組成，q由x'x的特征向量組成，Δ為對角線矩陣，對角線為矩陣x的特征值；

(3.3)利用公式

W＝qp'y (3)

計算自變量對第j個因變量的影響權重W。

(4)取步驟(2)和步驟(3)選取自變量的并集作為建模自變量。

(5)通過離群點分析法剔除氣動力六分量明顯不合理的數據點，根據剩余數據點通過多元高次交互回歸建立氣動力數據模型。

多元二次交互回歸建立氣動力數據模型的實現方式如下：

其中，[x₁ x₂ x₃ x₄]為選取的自變量，對應于馬赫數Ma、攻角α、舵偏角L、舵偏角R，y為因變量Cx，w₀、w_s、分別為方程零次項系數、一次項系數、二次項系數、交互項系數，M為自變量個數，等式右側第三項交互項中s≠j。可以通過最大似然法，基于樣本點數據，求解最優化問題(其中X是自變量x_s的一次項、二次項和交互項組成的向量、W是方程系數組成的矩陣)得到模型的方程系數，從而模擬自變量和因變量之間關系的數學表達形式。

(6)從樣本點數據集合中選取80％為訓練集，剩余的20％為測試集，根據訓練集中的數據，利用氣動力數據模型計算預測值，并與測試集比對，利用如下公式計算平均相對誤差MAPE：

其中pred_i為第i個樣本的預測值，true_i為第i個樣本在實際測試集中的值，N為樣本總數。

(7)如果MAPE小于等于5％，則氣動力數據模型合適，氣動特性處理結束，如果MAPE大于5％，則氣動力數據模型不合適，返回步驟(2)，在步驟(2)中補充選取拋棄自變量中前2/3的自變量，在步驟(3)中補充選取拋棄自變量中前2/3的自變量，直到MAPE小于等于5％。

為了進一步保證氣動模型的精準度，可以在步驟(6)中分五次選取不同的數據作為測試集，分別計算MAPE，如果五次的MAPE均小于等于5％，則氣動力數據模型合適，否則認為氣動力數據模型不合適。

當氣動力數據模型不合適時，通過步驟(2)和步驟(3)補充選取自變量后，在步驟(5)中采用更高次的回歸方法進行建模，可以以1為步進量逐漸增加次數。

實施例：

以某面對稱高速再入飛行器為例，該飛行器如圖2所示：

表1列出了該飛行器氣動數據中的馬赫數、攻角、側滑角和舵偏角度，共計15360個狀態點(馬赫數8個*攻角40個*側滑角3個*舵偏角16個＝15360個樣本點)。

表1氣動數據狀態表

本實施例中考慮的自變量X(狀態參量)包括馬赫數Ma、攻角a、側滑角b、舵偏角L、R、r，考慮的因變量y包括氣動力三分量Cx、Cy、Cz和氣動力矩三分量U、V、W。自變量和因變量之間組成變量對。

通過公式(1)進行氣動特性相關系數計算，使用熱力圖對相關系數矩陣進行可視化，結果如圖3所示。圖中展示的是相關系數矩陣(對稱矩陣)的元素值的大小，左下角為餅圖展示，對應的右上角為數值展示。左下角，餅圖的陰影面積越大，表明相關系數越大，每一個餅圖表示其所在列的變量對其所在行的變量的相關性；右上角，正系數代表正相關，負系數代表負相關，括號中的范圍為相關系數95％的置信區間。

通過公式(2)(3)計算自變量對因變量的權重系數。以自變量對氣動力Cx的權重系數計算為例，從圖4可見，對于給定的氣動數據，變量r和b對氣動力Cx的相對重要性較小，因此考慮在建模的過程中忽略其對因變量的影響，以提高建模的效率。

按相關系數從大到小的順序對自變量排序，選取前2/3的自變量作為集合1，按權重系數從大到小的順序對自變量排序，選取前2/3的自變量作為集合2，取集合1和集合2的并集作為建模自變量，剔除不合理數據點后通過多元高次交互回歸算法，建立多元、高次、且考慮了交互項的回歸模型，定量分析因變量和自變量之間的關系，把自變量的高次冪與因變量之間的關系考慮到模型中，并對自變量內部之間的關聯關系對因變量造成的影響進行建模。

為了保證預測結果的可信度，進行5重交叉驗證，每次取數據集的80％為訓練集，剩余20％的部分為測試集，五次測試集均不相同。并使用公式(4)計算平均相對誤差MAPE，如果五次的MAPE均小于等于5％，則氣動力數據模型合適，否則認為氣動力數據模型不合適。當氣動力數據模型不合適，補充選取拋棄的自變量，直到MAPE小于等于5％。

下面分別采用了幾種回歸模型進行建模，并進行誤差分析。首先給出最簡單的一階回歸模型，不考慮交互項，參數估計結果如下：

根據該參數構建氣動力數據模型，進行預測，最終得到MAPE值為10.37％。

考慮了交互項的一階回歸預測：有些自變量之間是具有很強的相關性的，因此在進行回歸分析時考慮它們的相關性可以提高預測的精度。參數估計結果如下所示：

根據該參數構建氣動力數據模型，進行預測，MAPE值降低到了8.42％。

考慮了交互項的高階回歸預測：進一步增加模型的復雜度，考慮自變量的冪次，構造高階回歸預測模型，參數估計結果如下所示：

MAPE值降低到了4.67％。

上述過程說明考慮了交互項的高階回歸模型預測精度更高，因此，當氣動力數據模型不合適時，應該采用更高次的回歸方法進行建模，以降低平均相對誤差。

應用本發明方法建立的氣動力數據模型得到的預測值與實際值的平均相對誤差以及應用傳統氣動數據處理方法得到的預測值與實際值的平均相對誤差對比圖如圖5所示，圖中HORAC對應于本發明方法，線性回歸、高階線性以及支持向量基對應于傳統氣動數據處理方法，可以看出，本發明顯著提高了氣動數據使用的準確度。

本發明基于空氣動力學原理和數據挖掘算法給出了飛行器的氣動特性數據處理算法。該方法通過分析氣動特性變化的主要影響因素和飛行器整體氣動特性變化規律，給出了高精度的氣動力數據模型，根據給出的氣動力數據模型以及樣本點數據能夠獲得飛行器設計空間的所有氣動特性數據，且與實際值誤差較小，從而顯著提高氣動特性分析的效率和使用準確度。

本發明說明書中未作詳細描述的內容屬本領域技術人員的公知技術。