一種用于電力系統經濟調度的分布式拍賣算法的制作方法

本發明屬于電力系統優化調度領域，具體是用拍賣算法來解決電力系統經濟調度問題。

背景技術：

電力系統經濟調度的任務是在滿足系統安全和電能質量要求的前提下盡可能提高系統運行的經濟性。求解電力系統經濟調度的方法可分為集中式方法和分布式方法。傳統的集中式方法例如迭代法和內點法，這兩種傳統方法在成本函數為凸性的情況下才能使用。盡管凸函數適合經濟調度的初步分析，但是凸函數求解效果不是很好，因為實際成本函數往往是非凸的。用于處理非凸性的經濟調度的方法一般是智能算法，其中包括遺傳算法(GA)、粒子群算法(PSO)等。在處理非凸性經濟調度問題時，這些算法是有效的，但這些算法都是集中式的；這種集中控制需要高帶寬通信基礎設施和高水平的連接，往往由于單獨節點故障導致整體出現建模誤差，導致系統可靠性受到影響。在智能電網環境下，決策過程正由集中式向分布式框架發展。本發明提出的拍賣算法是分布式的，具有即插即用的特點，并且非常適合大量分布式電源接入的情形，不易受網絡拓撲結構的影響，它消除了對集中控制的要求，能有效利用有限信息傳輸的稀缺的通信設施，使得整個系統具有更好的容錯性。

技術實現要素：

本發明的目的在于解決電力系統經濟調度問題，能夠高效率的解決負荷在機組間分配問題，降低系統發電成本，克服集中式算法容錯性差等弊端。

實現本發明的技術方案如下：

一種用于電力系統經濟調度的分布式拍賣算法，

在開始拍賣算法前，對每個發電機組的有功功率進行初始化，包括：首先根據系統總負荷要求確定各個發電機組的初始有功功率，其中p_i代表發電機組i的有功功率，P_D代表系統總負荷，p_imax和p_imin分別代表發電機組i有功功率最大值及最小值，N為發電機組總數；

拍賣算法過程主要包括：報價評估、協商、決議及交換；在執行過程中包含兩個時間層次，在第一時間層次內進行報價評估和協商，在第二時間層次內執行決議及交換；在第一時間層次內進行一次報價評估和協商后進入第二時間層次，在第二時間層次內進行N/2的最大整數次(每個機組都至多參與一次功率交換，所以將第二時間層次的次數設置為N/2最大整數次)決議及交換后再進入第一時間層次內進行報價評估及協商。

進一步地，所述報價評估中需要對每個發電機組進行以下計算：

其中，f_i代表發電機組i的發電成本，f_i＝a_i·p_i²+b_i·p_i+c_i，a_i,b_i,c_i是發電機組i的耗量特性系數，s代表在拍賣過程中交換的有功功率，π_i代表發電機組i的有功功率從p_i增加到p_i+s時所增加的發電成本，μ_i代表發電機組i的有功功率從p_i減少到p_i-s時所減少的發電成本。

進一步地，所述協商中引入評估差異值δ_ij，δ_ij＝μ_j-π_i；當δ_ij>0時，代表當在發電機組i,j之間形成一次拍賣，即發電機組i的有功功率增加s，發電機組j的有功功率減少s時，能夠減少的發電成本為δ_ij。

進一步地，所述決議與交換：對每個發電機組進行報價評估以及在每兩個發電機組之間計算評估差異，將評估差異值進行降序排列，在形成最大的評估差異值的兩個發電機組之間進行有功功率交換，即p_i←p_i+s,p_j←p_j-s，形成新的有功功率。

進一步地，在第二時間層次內，每個發電機組至多參與一次功率交換，將第二時間層次的次數設置為N/2的最大整數次，在每執行過一次交換后，將與已經執行了交換步驟的發電機組有關的評估差異值設置為0，再在剩余的評估差異值中尋找最大值來確定接下來要執行交換的發電機組。

進一步地，所述交換的有功功率s為離散變量，并且s＝r·p_D/100；其中，r是百分比變量，r＝[0.1,0.2,0.3,0.4,0.5,1…]。

進一步地，所述拍賣算法為雙邊拍賣，每個參與拍賣的發電機組既有可能成為拍賣方也可能成為競拍方，選擇的依據是在決議及交換中決定的，提供交換有功功率s的發電機組作為拍賣方，接受交換有功功率s的發電機組作為競拍方。

本發明的有益效果：

(1)本算法是分布式的，不易受電力網絡拓撲結構變化的影響，而且它具有可拓展性，并能夠容納大量分布式電源的接入，具有即插即用的特點。

(2)它消除了對集中控制的要求，不易受單獨節點故障的影響，能有效利用有限信息傳輸的稀缺的通信設施，使得整個系統具有更高的容錯性和可靠性。

(3)在系統中可以對調度任務進行快速有效的分配，實現發電機組間有功功率快速、有效的分配，具有較好的電力系統經濟調度優化效果。

附圖說明

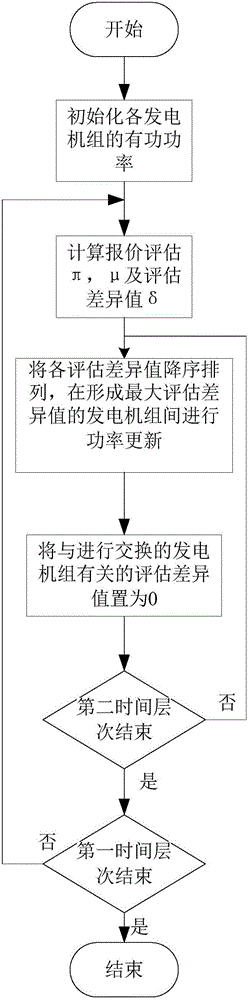
圖1是基于分布式拍賣算法的電力系統經濟調度的流程圖。

圖2是基于分布式拍賣算法的電力系統經濟調度時間層次軸，k代表第二時間層次執行的次數，每次k都進行一次決議與交換，一共進行k₀次，其中k₀＝N/2的最大整數，q是第一時間層次執行次數，一般情況下整個拍賣過程中第一時間層次內進行15-20次報價評估及協商即能達到優化結果。

具體實施方式

電力系統經濟調度問題是在滿足電網負荷要求和發電機組有功功率限制的條件下，使系統的發電成本最小。目標函數可以表示為：

其中，f(p)為系統的發電成本；f_i(p_i)為發電機組i的發電成本函數，p_i為發電機組i的有功功率；N為發電機組的總數。

一般情況下，發電機組i的發電成本f_i(p_i)表示為有功功率的二次函數形式：

f_i(p_i)＝a_i(p_i)²+b_ip_i+c_i

式中，a_i，b_i，c_i為發電機組i的耗量特性系數。

約束條件

(1)系統的有功功率平衡約束：

式中，p_D為系統總負荷。

(2)發電機組有功功率上下限的約束

p_imin≤p_i≤p_imax

式中，p_imax和p_imin分別代表發電機組i有功功率最大值及最小值。

下面結合附圖和具體實施例對本發明作進一步說明。

如圖1和圖2所示，本發明將分布式拍賣算法應用于電力系統經濟調度的實現包括：拍賣算法過程主要包括三大步驟：報價評估、協商、決議及交換；在執行過程中包含兩個時間層次，在第一時間層次內主要進行報價評估和協商，在第二時間層次內執行決議及交換；在第一時間層次內進行一次報價評估和協商后進入第二時間層次，在第二時間層次內進行N/2(N為發電機組總數)次決議及交換后再進入第一時間層次內進行報價評估及協商；一般情況下整個拍賣過程中第一時間層次內進行15-20次報價評估及協商即能達到優化結果。

在開始拍賣算法前，對每個發電機組的有功功率進行初始化，具體地：首先根據確定各個發電機組的初始有功功率，其中p_i代表發電機組i的有功功率，P_D代表系統總負荷，p_imax和p_imin分別代表發電機組i有功功率最大值及最小值。

所述算法中的報價評估中需要對每個發電機組進行以下計算：

其中，f_i代表發電機組i的發電成本，f_i＝a_i·p_i²+b_i·p_i+c_i，a_i,b_i,c_i是發電機組的耗量特性系數，s代表在拍賣過程中的交換功率，π_i代表發電機組i的有功功率從p_i增加到p_i+s時所增加的發電成本，μ_i代表發電機組i的有功功率從p_i減少到p_i-s時所減少的發電成本。

所述協商中引入評估差異值δ_ij，δ_ij＝μ_j-π_i；當δ_ij>0時，代表當在發電機組i,j之間形成一次拍賣時，即發電機組i的有功功率增加s，發電機組j的有功功率減少s時，能夠使發電成本減少δ_ij。

所述決議與交換：對每個發電機組進行報價評估以及在每兩個發電機組之間計算評估差異，由于評估差異值越大，能夠減少的發電成本越多，因此將評估差異值進行降序排列，在形成最大的評估差異值的兩個發電機組之間進行有功功率交換，即p_i←p_i+s,p_j←p_j-s，形成新的有功功率。在第二時間層次內，每個發電機組都只能至多參與一次功率交換，所以將第二時間層次的次數設置為N/2，在每執行過一次交換后，將與已經執行了交換步驟的發電機組有關的評估差異值設置為0，再在剩余的評估差異值中尋找最大值來確定接下來要執行交換的發電機組。

進一步，所述的交換的有功功率s：s是一個離散變量，并且s＝r·p_D/100，其中，r是百分比變量，r＝[0.1,0.2,0.3,0.4,0.5,1…]，不同的r對應不同的s，形成的優化結果也不同；最終在求得的幾組優化結果中選擇使系統發電成本最低的情況作為最優結果。

進一步，所述的分布式拍賣算法：本發明拍賣算法為雙邊拍賣，也就是每個參與拍賣的發電機組既有可能成為拍賣方也可能成為競拍方，具體選擇哪個發電機組作為拍賣方或競拍方是在決議及交換中決定的，提供交換功率s的發電機組作為拍賣方，接受交換功率s的發電機組作為競拍方。

實施例：

本發明提出的分布式拍賣算法應用于電力系統經濟調度可通過Matlab編程實現。下面為一組實例，運用本發明中的算法取得的結果。表1是發電機組的參數，表2是運用本發明中的算法調度后所得結果，表3為不同算法的調度結果比較，在此算例中，當r＝0.3時成本最低。

表1發電機組特性參數表 p_D＝2630MW

表2調度結果

表3不同算法優化15機系統結果比較

上文所列出的一系列的詳細說明僅僅是針對本發明的可行性實施方式的具體說明，它們并非用以限制本發明的保護范圍，凡未脫離本發明技藝精神所作的等效實施方式或變更均應包含在本發明的保護范圍之內。