區間值型直覺模糊小腦神經網絡模型的制作方法

本發明涉及一種區間值型直覺模糊小腦神經網絡模型。

背景技術：

小腦神經網絡模型(CMAC-Cerebellar Model Articulation Controller)是一種表達復雜非線性函數的表格查詢型自適應神經網絡，該網絡可通過學習算法改變表格的內容，具有信息分類存儲的能力。CMAC已被公認為是一類聯想記憶網絡的重要組成部分，能夠學習任意多維非線性映射，CMAC算法被證明可有效地用于非線性函數逼近、動態建模、控制系統設計等。

然而，現有的小腦神經網絡模型采用傳統的模糊集合，對不確定性問題的模糊語言描述有限，精確度不夠；另外，現有小腦神經網絡模型還具有收斂性和精確度有待進一步提高、計算量大、模型降型過程復雜等缺點。

技術實現要素：

本發明提供一種區間值型直覺模糊小腦神經網絡模型，可有效解決上述問題。

一種區間值型直覺模糊小腦神經網絡模型，所述區間值型直覺模糊小腦神經網絡模型包括按照邏輯順序連接的輸入空間聯想記憶空間規則空間權重空間降解空間以及輸出空間O，其中，所述輸入空間由區間值型直覺模糊規則的輸入變量組成；所述聯想記憶空間為由基函數構成的區間值型直覺模糊規則的前件組成；所述規則空間表示為其中所述權重空間為對應區間值型直覺模糊規則的后件組成；所述降解空間為根據w_jko r_jk的線性變化的關系獲得的解模糊化算子其中，所述輸出空間O為多維區間值型直覺模糊小腦神經網絡模型的輸出O_o＝a×y_o⁺+b×y_o^-，其中a、b為常數。

作為進一步改進的，所述數據樣本是基于區間值型的直覺模糊集合。

作為進一步改進的，所述基函數為高斯函數、三角函數或鐘型函數。

作為進一步改進的，所述多維區間值型直覺模糊小腦神經網絡模型的模糊規則為：

for i＝1，2，…，n_i，j＝1，2，…，n_j，k＝1，2，…，n_k，λ＝1，2，…，n_λ，and o＝1，2，…，n_o

其中：R^λ是第λ條區間值型直覺模糊規則,是第λ條區間值型直覺模糊規則的第i個直覺模糊區間輸入變量,是第λ條區間值型直覺模糊規則的前件部分，與第j層、第k個模塊的第i個輸入相對應,是第λ條區間值型直覺模糊規則的第o個網絡輸出,是第λ條區間值型直覺模糊規則的后件部分，n_i是輸入變量維數，n_j是小腦神經網絡的層數,n_k是每一層的模塊數,n_o是輸出維數。

作為進一步改進的，當“隸屬度＝1-非隸屬度”時，區間值型直覺模糊小腦神經網絡模型結構可轉化成傳統的1型模糊小腦神經網絡的結構形式。

作為進一步改進的，當網絡的結構參數n_j＝1，n_k＝1時，區間值型直覺模糊小腦神經網絡模型結構可轉化成區間值型直覺模糊神經網絡的結構形式。

作為進一步改進的，當直覺模糊集合的猶豫度為0，且網絡結構參數所有層的基函數個數n_b＝1時，區間值型直覺模糊小腦神經網絡模型結構可轉化成1型模糊神經網絡的結構形式。

本發明提供的所述區間值型直覺模糊小腦神經網絡模型，具有以下優點：

1、將模糊小腦神經網絡與Atanassov的直覺模糊集相結合，提出符合此架構的模糊規則庫，構造新的性能更完善的MIMO模糊神經網絡結構；

2、網絡結構的參數可以靈活設置和選擇，通過結構參數的選擇，可以將該模型的結構簡化成其他模式的結構形式，如模糊神經網絡、區間型模糊神經網絡和小腦神經網絡等，在模型結構上具有一定的廣義性；

3、根據參數線性關系，避免采用傳統的模型降型算法KM算法，減少了模型降型、解模糊化過程的計算量；

4、通過對參數的自適應調節，提高模型自適應能力，獲得更加快速的收斂性和更加良好的穩定性。

附圖說明

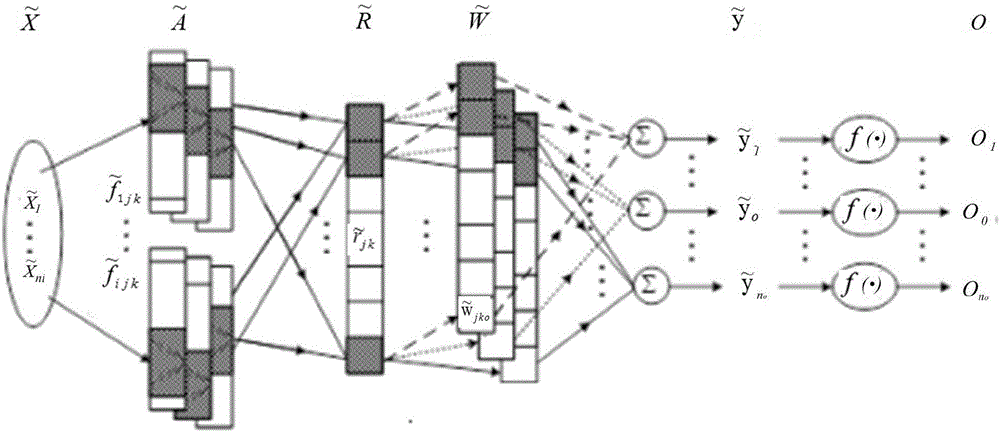
圖1為本發明實施例提供的多維區間值型直覺模糊小腦神經網絡的結構示意圖。

具體實施方式

下面結合附圖和實施例對本發明作進一步的詳細說明。可以理解的是，此處所描述的具體實施例僅用于解釋本發明，而非對本發明的限定。另外還需要說明的是，為了便于描述，附圖中僅示出了與本發明相關的部分而非全部結構。

提出小腦神經網絡與Atanassov的直覺模糊集相結合的模糊規則；構造廣義結構的多維區間值型直覺模糊小腦模型神經網絡模型。

請參照圖1，一種區間值型直覺模糊小腦神經網絡模型，所述區間值型直覺模糊小腦神經網絡模型包括按照邏輯順序連接的輸入空間聯想記憶空間規則空間權重空間降解空間以及輸出空間O。

所述多維區間值型直覺模糊小腦神經網絡模型的模糊規則為：

for i＝1，2，…，n_i，j＝1，2，…，n_j，k＝1，2，…，n_k，λ＝1，2，…，n_λ，and o＝1，2，…，n_o

其中：R^λ是第λ條區間值型直覺模糊規則,是第λ條區間值型直覺模糊規則的第i個直覺模糊區間輸入變量,是第λ條區間值型直覺模糊規則的前件部分，與第j層、第k個模塊的第i個輸入相對應,是第λ條區間值型直覺模糊規則的第o個網絡輸出,是第λ條區間值型直覺模糊規則的后件部分，n_i是輸入變量維數，n_j是小腦神經網絡的層數,n_k是每一層的模塊數,n_o是輸出維數。

所述輸入空間由區間值型直覺模糊規則的輸入變量組成。

所述聯想記憶空間由基函數構成的區間值型的直覺模糊規則前件基函數可以是高斯函數、三角函數、鐘型函數等的形式。通過這一空間，將輸入變量映射到區間值型直覺模糊集合中。

所述規則空間表示為將各個輸入變量的區間值型直覺模糊集合進行排列組合，用T-norm進行模糊AND運算，其中

所述權重空間為對應區間值型直覺模糊規則的后件組成。

所述降解空間為降型和解模糊化的過程。根據w_jko r_jk的線性變化的關系，獲得解模糊化算子其中，

所述輸出空間O為多維區間值型直覺模糊小腦神經網絡模型的輸出O_o＝a×y_o⁺+b×y_o^-，其中a、b為常數。

多維區間值型直覺模糊小腦神經網絡的廣義結構：

由于采用的是Atanassov的直覺模糊集合，所以，當“隸屬度＝1-非隸屬度”時，區間值型直覺模糊小腦神經網絡結構可以轉化成傳統的1型模糊小腦神經網絡的結構形式；

當網絡的結構參數n_j＝1，n_k＝1時，區間值型直覺模糊小腦神經網絡結構可以轉化成區間值型直覺模糊神經網絡的結構形式；

當直覺模糊集合的猶豫度為0，且網絡結構參數所有層的基函數個數n_b＝1時，區間值型直覺模糊小腦神經網絡結構可以轉化成1型模糊神經網絡的結構形式。

自適應有監督學習

需要調節的網絡參數用z統一表示，包括聯想記憶空間基函數的參數和權重空間的權重值等。當網絡參數z按照學習變化率公式在線實時調整時，使追蹤誤差e快速、準確地逼近于0，完成有監督的自適應調節，確保多維區間值型直覺模糊小腦神經網絡獲得更加快速的收斂性和更加良好的穩定性。

注意，上述僅為本發明的較佳實施例及所運用技術原理。本領域技術人員會理解，本發明不限于這里所述的特定實施例，對本領域技術人員來說能夠進行各種明顯的變化、重新調整和替代而不會脫離本發明的保護范圍。因此，雖然通過以上實施例對本發明進行了較為詳細的說明，但是本發明不僅僅限于以上實施例，在不脫離本發明構思的情況下，還可以包括更多其他等效實施例，而本發明的范圍由所附的權利要求范圍決定。