一種渦輪葉片熱障涂層厚度優化設計方法與流程

本發明屬于表面涂層防護技術領域，具體涉及一種渦輪葉片熱障涂層厚度優化設計方法。

背景技術：

熱障涂層(TBCs)是一種先進的陶瓷金屬多層材料系統，在現代渦輪發動機中應用十分廣泛。通過在發動機燃燒室、渦輪葉片等高溫熱端部件表面涂覆具有低熱導率的TBCs，一方面可降低金屬部件表面溫度或進一步提高發動機渦輪葉片燃氣入口溫度，另一方面可使金屬部件免受高溫燃氣的腐蝕和氧化，從而實現延長熱端部件服役壽命和提高發動機效率的目的。以燃氣輪機渦輪葉片為例，TBCs和葉片內部冷卻的聯合作用可有效降低高溫合金表面溫度100～300℃，使得合金基底能夠在高于其熔點溫度的環境下長期穩定服役。

TBCs主要由陶瓷層、金屬粘接層、高溫合金基底、以及在陶瓷層/粘接層界面形成的熱生長氧化層構成。TBCs各層材料間存在較大的性能差異，使得制備或高溫服役過程中在涂層內部產生顯著的熱失配應力。較高的熱失配應力可能誘發涂層內部裂紋的萌生和擴展，進而導致涂層的剝離失效。因此，應力水平是影響涂層服役壽命的重要因素。TBCs的隔熱作用主要依靠表面陶瓷層實現，在給定熱流密度的情況下，陶瓷層的熱導率和厚度是TBCs隔熱性能的兩個決定性因素。在選定陶瓷層材料后，TBCs的隔熱性能隨著陶瓷層厚度的增加而提高，然而涂層內部的應力水平也可能不斷升高。對陶瓷層厚度進行設計時，在滿足涂層隔熱性能的情況下需控制其內部的應力水平，并有必要考慮涂層的制備成本。因此，TBCs結構設計是一個在滿足涂層高隔熱性能、低應力水平和低制備成本等約束條件下的多目標優化問題。

對渦輪葉片表面涂覆的TBCs進行厚度優化設計，有助于保證涂層服役安全，并提高其性能及使用效率。然而，當前的現有技術只能定性給出渦輪葉片TBCs厚度的大致分布，無法實現準確的厚度分布優化設計，缺少針對TBCs厚度設計優劣的評價。因此，隨著表面涂層技術的不斷快速發展，在工程應用中迫切需要發展渦輪葉片TBCs的厚度優化設計方法。

技術實現要素：

本發明的目的在于提供一種渦輪葉片熱障涂層厚度優化設計方法，該方法能夠簡單高效的進行優劣的定量評價，有助于保證涂層服役安全和提高涂層使用效率。

本發明是通過以下技術方案來實現：

一種渦輪葉片熱障涂層厚度優化設計方法，包括以下步驟：

步驟1：確定TBCs各層厚度；

TBCs包含陶瓷層、粘結層及熱生長氧化層，為陶瓷層、粘結層及熱生長氧化層賦予厚度值；

陶瓷層厚度為k×100μm，k為分析次數的編號，即步驟1至步驟6的重復次數，k＝1,2,…,10；(為了分析不同陶瓷層厚度的結果，步驟1-6需要重復10次，而每次厚度的確定是通過k*100得到的，k就是重復次數)粘接層厚度為100μm～250μm；熱生長氧化層厚度為1μm～10μm；

步驟2：建立含TBCs渦輪葉片的三維有限元模型；

三維有限元模型由葉片合金基底和均勻厚度的TBCs構成，TBCs涂覆于渦輪葉片的葉身外表面和葉根平臺的上表面；所述均勻厚度TBCs是指涂層覆蓋區域內的陶瓷層厚度均相同，TBCs各層厚度由步驟1給定；

步驟3：對三維有限元模型進行網格劃分；

步驟4：對劃分網格后的三維模型進行熱-力耦合分析，獲得含TBCs渦輪葉片的整體溫度場和應力場分布；

步驟5：選取葉片涂層區域內的代表節點；

代表節點是指能夠反映各局部區域的溫度和應力狀態特征的代表性節點，代表節點位置在不同分析對應的三維有限元模型中一致；

步驟6：提取并記錄所有代表節點所在位置的厚度方向，陶瓷層的最大應力值和溫度差；

步驟7：判斷均勻厚度TBCs模型是否分析完成；

判斷k≤10是否成立，若成立則重復步驟1至步驟6；否則，按照步驟8進行；

步驟8：對步驟5中選定的任意代表節點i，i＝1,2,…,110，根據公式(1)分別計算第k次分析對應的有限元模型中該代表節點位置的目標函數值：

公式(1)中，是第k次分析中代表節點i位置處的目標函數，是第k次分析中代表節點i位置處陶瓷層內最大應力，是第k次分析中代表節點i位置處陶瓷層內的溫度差，是第k次分析中代表節點i位置處陶瓷層的厚度，w_β是性能權重系數，取w_β＝0.6；w_h是厚度權重系數，取w_h＝0.4；

步驟9：獲得葉片陶瓷層厚度的理想分布，對于任意代表節點，求得使其目標函數值最小時的最佳陶瓷層厚度；

步驟10：根據步驟9中獲得的葉片陶瓷層厚度理想分布，劃分TBCs厚度分布子區域，子區域的陶瓷層厚度與其包含的代表節點中最佳陶瓷層厚度的最大值相同；

步驟11：計算葉片TBCs厚度分布的總目標函數；根據步驟10中給出的子區域陶瓷層厚度分布，并結合公式(1)計算得到的目標函數值，按照公式(2)計算葉片TBCs厚度分布的總目標函數值：

公式(2)中，G_obj是當前TBCs厚度分布的總目標函數值，g_i是代表節點i位置處的目標函數；

步驟12：確定TBCs厚度分布方案；

重復步驟10和步驟11，不斷調整子區域大小，直至公式(2)計算獲得的G_obj最小，獲得渦輪葉片TBCs厚度分布的優化設計方案。

步驟4中，所述熱-力耦合分析是通過有限元軟件ABAQUS完成，該過程包括以下步驟：

a.對所述三維有限元模型中的合金基底和TBCs分別賦予材料屬性；

b.對所述三維有限元模型中的TBCs外表面施加高溫邊界條件，對葉片冷卻通道表面施加冷卻溫度邊界條件；

c.利用ABAQUS提供的熱-力耦合分析模塊，對有限元模型進行分析計算；

d.計算完成后，在ABAQUS后處理模塊輸出計算結果，獲得含TBCs渦輪葉片的整體溫度場和應力場分布。

步驟5中，代表節點針對所述三維有限元模型，在ABAQUS后處理模塊中，從葉身吸面選取均勻分布的50個代表節點，從葉身壓面選取均勻分布的50個代表節點，從葉根平臺選取均勻分布的10個代表節點。

步驟6所述厚度方向指葉片表面的法線方向；所述溫度差是指陶瓷層外表面與陶瓷層/熱生長氧化層界面之間的溫度差值。

步驟9中，所述最佳陶瓷層厚度指在此代表節點區域涂覆該厚度的陶瓷層時，獲得隔熱性能、應力水平和制備成本之間的最佳協調；根據所有代表節點區域的最佳陶瓷層厚度結果，獲得葉片陶瓷層厚度的理想分布。

步驟10中，劃分TBCs厚度分布子區域，是將葉身壓面分為3個子區域，葉身吸面分為3個子區域，葉根平臺分為1個子區域；所述葉身壓面和吸面的子區域沿葉片高度方向劃分，每個子區域內包含多個代表節點。

與現有技術相比，本發明具有以下有益的技術效果：

本發明公開的渦輪葉片熱障涂層厚度優化設計方法，通過在渦輪葉片上選取均勻分布的代表節點，以代表節點位置的溫度和應力結果來反映各局部區域的狀態，將復雜葉片的TBCs厚度分析等效為對有限數量的代表節點位置的厚度優化設計，大大減少了分析計算量；將復雜的葉片TBCs厚度設計定義為明確的多目標優化問題，建立數學公式來反映高隔熱性能、低應力水平和低制備成本的設計目標，通過引入多目標優化算法計算得到每個代表節點位置的最佳陶瓷層厚度，將總目標函數值作為葉片TBCs厚度的優化設計和評價參數，從而能夠定量評價TBCs厚度分布方案的優劣，克服現有方法僅能定性評價的缺點。因此，本發明的渦輪葉片熱障涂層厚度優化設計方法，可以簡單高效的進行TBCs厚度優化設計，并能實現設計方案優劣的定量評價，有助于保證涂層服役安全和提高涂層使用效率。

附圖說明

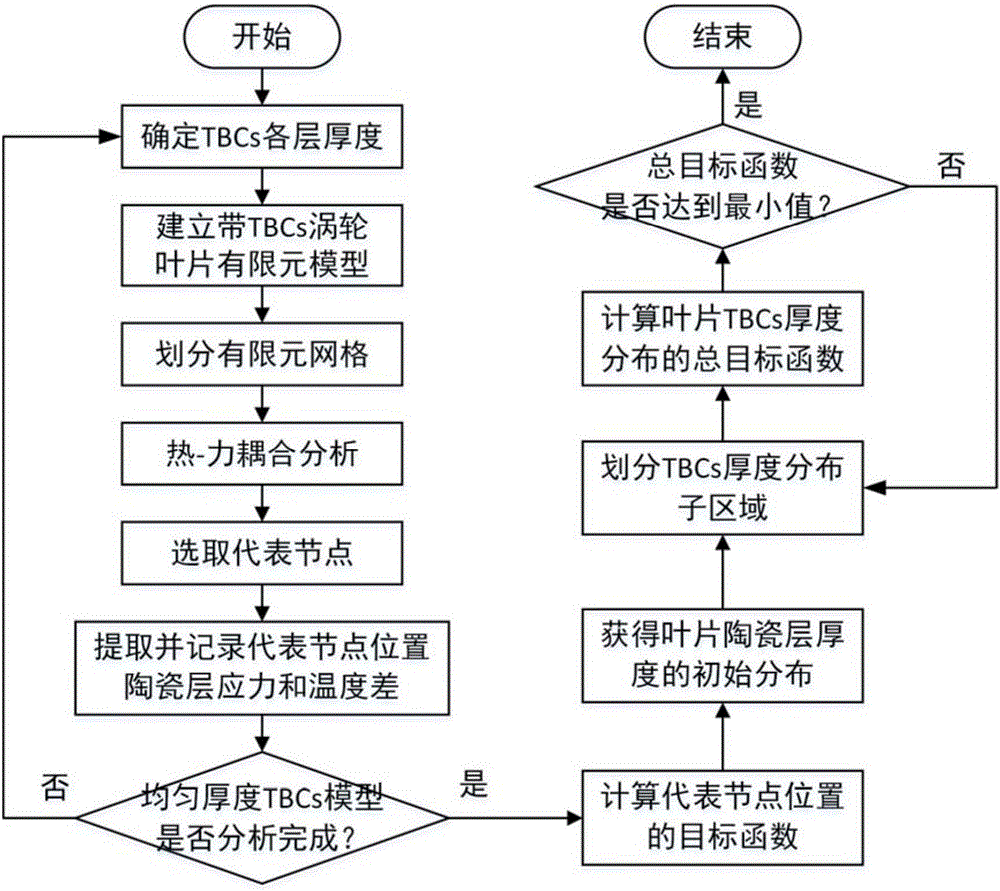
圖1是燃氣輪機渦輪葉片熱障涂層厚度優化設計方法流程圖；

圖2是燃氣輪機渦輪葉片模型圖；

圖3是葉身壓面代表節點分布及厚度子區域劃分；

圖4是葉身吸面代表節點分布及厚度子區域劃分；

圖5是葉根平臺代表節點分布；

圖6是葉身陶瓷層厚度分布結果。

圖中，1-葉身壓面，2-葉身吸面，3-葉根平臺，4-陶瓷層，5-熱生長氧化層，6-金屬粘接層，7-高溫合金基底，8-代表節點，9-葉身壓面子區域1，10-葉身壓面子區域2，11-葉身壓面子區域3，12-葉身吸面子區域1，13-葉身吸面子區域2，14-葉身吸面子區域3，15-葉片冷卻通道。

具體實施方式

下面結合具體的實施例對本發明做進一步的詳細說明，所述是對本發明的解釋而不是限定。

本發明的優化設計流程如圖1所示，為了更好的理解本發明的技術方案，將以上優化設計方法應用于燃氣輪機渦輪葉片的TBCs厚度設計，渦輪葉片如圖2所示。

本實施例的具體過程包括以下步驟：

步驟1：確定TBCs各層厚度。

所述TBCs包含陶瓷層、粘接層和熱生長氧化層。選定陶瓷層厚度為k×100μm，其中k為分析次數的編號，即步驟1至步驟6的重復次數，k＝1,2,…,10。本實施例選定的粘接層厚度為150μm，選定熱生長氧化層厚度為5μm。

步驟2：建立含TBCs渦輪葉片的有限元模型。

采用有限元軟件ABAQUS建立含TBCs渦輪葉片的三維有限元模型。所述有限元模型由葉片合金基底和均勻厚度的TBCs構成，TBCs涂覆于渦輪葉片的葉身外表面和葉根平臺的上表面；所述均勻厚度TBCs是指涂層覆蓋區域內的陶瓷層厚度均相同，TBCs各層厚度由步驟1給定。

步驟3：對所述有限元模型劃分網格。

采用ABAQUS對有限元模型劃分網格。對于葉身和平臺的合金基底，劃分名義尺寸為1mm的六面體網格，單元類型為六面體單元C3D8R；合金基底的其余部分劃分名義尺寸為2mm的四面體網格，單元類型為四面體單元C3D4。葉片的陶瓷層在厚度方向劃分為5層六面體單元，熱生長氧化層在厚度方向劃分1層六面體單元，粘接層在厚度方向劃分2層六面體單元；所述厚度方向指葉片表面的法線方向。

步驟4：采用ABAQUS對所述有限元模型進行熱-力耦合分析，分析過程包括：

a.對所述有限元模型中的合金基底賦予材料屬性，本實施例中合金基底的彈性模量為220GPa，泊松比0.31，熱膨脹系數12.6×10^-6/℃^-1，熱導率11.5W/m℃；

b.對所述有限元模型中的陶瓷層賦予材料屬性，本實施例中陶瓷層的彈性模量為48GPa，泊松比0.1，熱膨脹系數9×10^-6/℃^-1，熱導率1.2W/m℃；

c.對所述有限元模型中的熱生長氧化層賦予材料屬性，本實施例中熱生長氧化層的彈性模量為400GPa，泊松比0.23，熱膨脹系數8×10^-6/℃^-1，熱導率10W/m℃；

d.對所述有限元模型中的粘接層賦予材料屬性，本實施例中粘接層的彈性模量為200GPa，泊松比0.3，熱膨脹系數13.6×10^-6/℃^-1，熱導率5.8W/m℃；

e.對所述有限元模型中的TBCs外表面施加1150℃的溫度邊界條件，對葉片冷卻通道表面施加700℃的溫度邊界條件；

f.對有限元模型進行熱-力耦合分析計算；

g.計算完成后，在ABAQUS后處理模塊輸出計算結果，獲得有限元模型的整體溫度場和應力場分布。

步驟5：選取葉片涂層區域內的代表節點。

所述代表節點是指可反映局部區域的溫度和應力狀態特征的代表性節點。在ABAQUS后處理模塊中，從葉身壓面選取圖3所示的50個均勻分布代表節點，從葉身吸面選取圖4所示的50個均勻分布代表節點，從葉根平臺選取圖5所示的10個均勻分布代表節點。所述代表節點位置在不同分析對應的有限元模型中一致。

步驟6：提取并記錄所有代表節點所在位置處，陶瓷層在厚度方向的最大應力值和溫度差。

在ABAQUS后處理模塊中，提取并記錄所有代表節點所在位置處，陶瓷層在厚度方向的最大應力值和溫度差。所述厚度方向指葉片表面的法線方向。所述溫度差是指代表節點所在位置處，陶瓷層外表面與陶瓷層/熱生長氧化層界面之間的溫度差值。

步驟7：判斷k≤10是否成立，若成立則重復步驟1至步驟6，否則按照步驟8進行。本實施例共需分析10種不同均勻陶瓷層厚度的葉片模型，用k表示分析次數的編號，也即步驟1至步驟6的重復次數，其中k＝1,2,…,10。

步驟8：對步驟5中選定的任意代表節點i(i＝1,2,…,110)，根據公式(1)分別計算第k次分析對應的有限元模型中該代表節點位置的目標函數值：

公式(1)中，是第k次分析中代表節點i位置處的目標函數，是第k次分析中代表節點i位置處陶瓷層內應力的最大，是第k次分析中代表節點i位置處陶瓷層的溫度差，是第k次分析中代表節點i位置處陶瓷層的厚度；w_β是性能權重系數，取w_β＝0.6；w_h是厚度權重系數，取w_h＝0.4。

步驟9：獲得葉片陶瓷層厚度的理想分布。

對于任意代表節點i，求得使其目標函數值達到最小時的陶瓷層厚度是代表節點i位置處的最佳陶瓷層厚度。所述最佳陶瓷層厚度指在此代表節點區域涂覆該厚度的陶瓷層時，可獲得隔熱性能、應力水平和制備成本之間的最佳協調。根據所有代表節點區域的最佳陶瓷層厚度結果，獲得葉片陶瓷層厚度的理想分布。

步驟10：劃分TBCs厚度分布子區域。

根據步驟9中獲得的葉片陶瓷層厚度理想分布，并結合制備工藝的可實現性，將葉身壓面分為3個子區域，葉身吸面分為3個子區域，葉根平臺分為1個子區域。所述葉身壓面和吸面的子區域沿葉片高度方向劃分，如圖3和圖4示意。所述子區域包含多個代表節點，這些代表節點的最佳陶瓷層厚度不盡相同；為此，對于任意給定的子區域，子區域內具有相同的陶瓷層厚度，指定陶瓷層厚度與其包含的代表節點中最佳陶瓷層厚度的最大值相同。

步驟11：計算葉片TBCs厚度分布的總目標函數。

根據步驟10中給出的子區域陶瓷層厚度分布，并結合公式(1)計算得到的目標函數值，按照公式(2)計算葉片TBCs厚度分布的總目標函數值：

公式(2)中，G_obj是當前TBCs厚度分布的總目標函數值，g_i是代表節點i位置處的目標函數。

步驟12：確定TBCs厚度分布方案。

重復步驟10和步驟11，不斷調整子區域大小，直至公式(2)計算獲得的G_obj最小，以此獲得渦輪葉片TBCs厚度分布的優化設計方案。

本實施例優化設計得到的葉身陶瓷層厚度分布如圖6所示，根據該厚度方案計算得到總目標函數值G_obj＝54.91；而均勻厚度分布方案中，陶瓷層厚度為400μm時G_obj＝70.25，優化設計方案的總目標函數值比均勻厚度方案降低了27.9％。由此可見，本發明的渦輪葉片熱障涂層厚度優化設計方法能夠明顯提高涂層使用效率，并提高涂層服役性能且降低制備成本。