局部形狀遷移指導的圖像對象共分割方法與流程

本發明屬于圖像處理、計算機視覺技術領域，是局部形狀遷移指導的圖像對象共分割方法。

背景技術：

給定包含相同語義類別對象的圖像集，圖像對象共分割技術主要考慮如何從中分割出共同的對象，以便開展圖像內容理解、對象檢測等更高層次的視覺理解工作。在2006年，Rother等人首次提出圖像對象共分割的概念，利用產生式模型在包含相同類別的圖像對上進行對象前背景分割，該方法使用高斯模型產生潛在前景直方圖，并將圖像對在前景直方圖的差異作為一項全局約束加入基于馬爾科夫隨機場的能量中，最后采用TRGC優化算法得到共分割結果。目前，多幅圖像的共分割大致分為兩個方向：基于統一模板學習的共分割和基于區域匹配的共分割。

基于統一模板學習的共分割方面，在2010年，Joulin等人提出了一種基于判別聚類的圖像對象共分割方法，他們將現有的單張圖像分割算法(歸一化分割)和對象檢測算法(核方法)集成到一個新的判別聚類框架中，目標是對多幅圖像進行前背景分割。首先，該方法為保持單幅特定圖片在空間和外觀上的一致性，利用像素點的坐標及RGB顏色值作為特征計算相似度矩陣，在得到標準化拉普拉斯矩陣L后采用類似歸一化分割的譜分割算法得到圖像內部的分割結果；其次，該方法為使同時分割的多幅圖像產生關聯，使用了基于正定核的判別聚類算法實現不同圖像之間前背景差異最大化；最后，該方法通過將空間一致性拉普拉斯矩陣L和判別聚類損失矩陣A進行組合，將多幅圖像的共分割轉化為一個組合優化問題，并通過將其松弛為連續的凸優化問題實現多幅圖像共分割。然而，當共分割對象的外觀模型復雜程度增大，或前景區域與背景區域十分相似時，共分割對象在全局形狀上的不一致性將導致很難學習到統一的模板用于前景對象的分割，此時基于統一模板學習的共分割方法便不能很好的區分前景對象與背景區域。

基于區域匹配的共分割方面，在2013年，Wang等人提出一種一致性泛函映射方法，通過計算圖像間在外觀上的關聯性實現多幅圖像的共分割，該方法包含三個部分。第一部分：將每幅圖像分割成超像素塊，并將每幅圖片表示為無向圖，圖中頂點表示超像素塊，圖中邊的權值由超像素塊公共邊的長度決定，通過給每個圖計算一個標準化的拉普拉斯矩陣為每幅圖片生成一個維度較低的泛函空間，同時分割結果表示成包含對象的超像素塊的集合。第二部分：將兩幅圖像之間的關聯性表達成線性泛函。第三部分：聯合優化分割函數產生分割結果，該過程需要匹配單幅圖像上的分割先驗，同時保持相鄰圖像間泛函映射時的一致性。該方法既可以實現無監督的共分割，也可以通過使用部分圖像的真實分割結果進行有監督的共分割。基于區域匹配的共分割方法在公開數據集上取得了令人滿意的結果，但前景對象在外觀發生較大變化時，會極大的影響最終的分割結果。

局部形狀遷移是一種廣泛應用于基于數據驅動的前背景分割方法，該方法能將真實分割結果遷移到測試圖像上，達到對單張測試圖像進行前背景分割的目的。在2015年，Yang等人提出了一種通過局部形狀遷移實現數據驅動下的對象分割方法，該方法首先輸入一幅測試圖像和多幅帶有真實分割結果的樣本圖像，然后采用Barnes在2010年提出的PatchMatch方法實現以局部patch塊為單位的多尺度圖像匹配，通過匹配結果為測試圖像上每一個局部patch塊得到在其他圖像上的近似局部patch塊，最后采用MRF能量函數得到最終分割結果。

在2013年，Kim等人提出了一種可變形的空間金字塔匹配算法(DSP)，解決了兩幅圖像間稠密像素點的匹配問題。該方法采用金字塔模型從整幅圖像，到網格單元再到單個像素點進行多尺度的匹配，將像素點匹配結果以水平位移和垂直位移的形式進行輸出。在國際公開數據集上的測試結果表明，該方法能為相同語義類別的像素點之間建立較好的匹配關系，為本方法中實現patch塊的匹配提供基礎。

在2000年，Roweis等人提出了一種局部線性嵌入的降維算法，并廣泛應用于圖像分割、圖像分類等計算機視覺領域。該算法包括三個主要步驟。第一步是為每個樣本點x_i尋找k個鄰近點，第二步是用k個鄰近點計算該樣本點的局部重建權重矩陣，所用誤差公式如下：

第三步是由該樣本點的局部重建權重矩陣將樣本點映射到低維空間中，映射條件如下：

上式中，y_i是樣本點x_i在低維空間的映射。

因此，前景對象姿態、位置、尺度發生較大變化時對象全局形狀的不一致性，極大的影響了現有的圖像對象共分割方法的分割效果，而本發明通過局部形狀遷移指導的方法，有效避免了因對象全局形狀的不一致帶來的問題。

技術實現要素：

本發明的目的是：克服對象全局形狀的不一致對圖像對象共分割結果的影響，提出了局部形狀遷移指導的圖像對象共分割方法，這種方法在標準測試數據集上有良好的表現，能夠較好的實現同一語義類別對象的分割。

為完成本發明的目的，本發明采用的技術方案是：

局部形狀遷移指導的圖像對象共分割方法，其中，包括如下步驟：

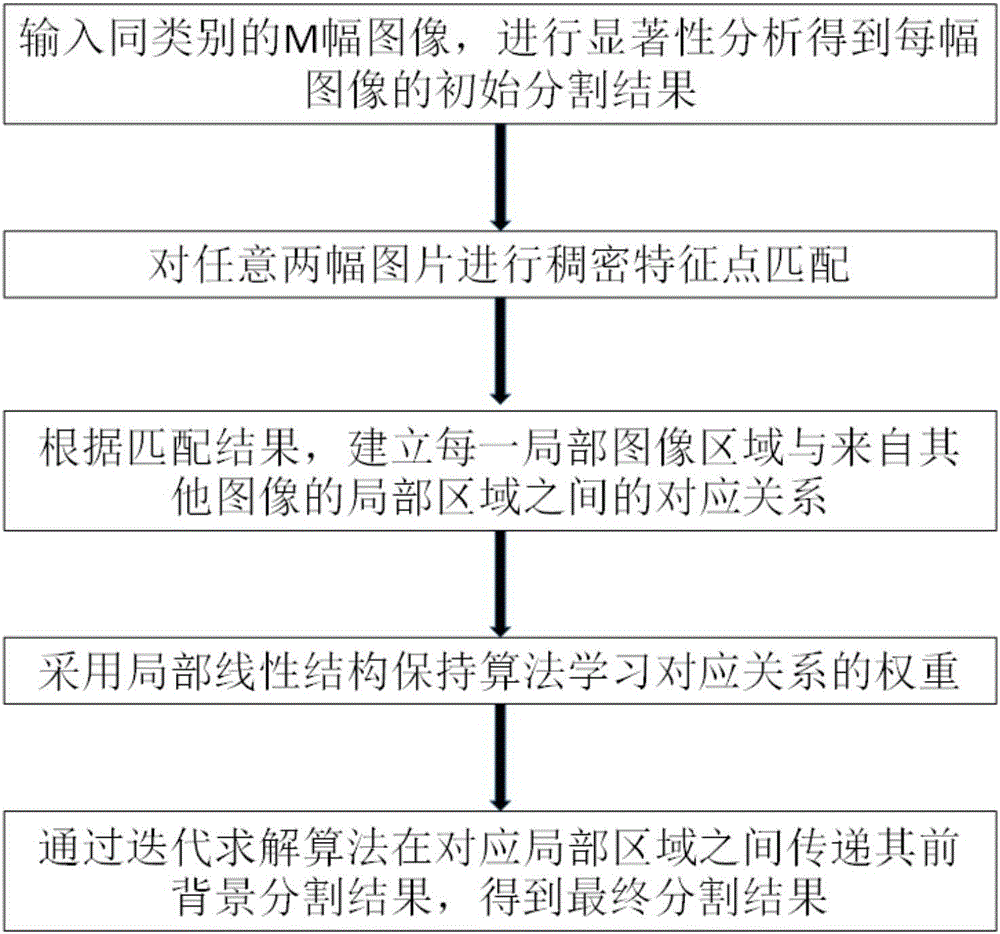
步驟(1)，圖像集預處理：輸入M幅包含相同語義類別對象的圖像，對每幅圖像進行顯著性分析，將顯著性檢測結果使用二倍均值做閾值得到mask圖，即為前背景初始分割結果，其中mask圖僅由0和1組成，1代表前景像素點，0代表背景像素點。

步驟(2)，對任意兩幅圖片進行稠密特征點匹配：針對每一幅圖像i(i＝1,2,...,M)，為圖像上每一個像素點生成128維的dense sift特征；將每一幅圖片i(i＝1,2,...,M)的dense sift特征與其他圖片j(j＝1,2,...,M且j≠i)的dense sift特征進行稠密特征點匹配，得到稠密特征點的水平位移h_ij和垂直位移v_ij。

步驟(3)，根據匹配結果，建立每一局部圖像區域與來自其他圖像的局部區域之間的對應關系：對每一幅圖像i，每間隔5個像素點選取一個17*17的patch塊，用中心像素點坐標表示該patch塊的位置，用中心像素點的sift特征描述子表示該patch塊的特征；使用步驟(2)中得到的水平位移h_ij和垂直位移v_ij，計算出每一個patch塊在其他圖像上與之對應的patch塊的位置；構建patch塊的對應關系有向圖，頂點代表patch，有向邊指向該patch塊在其他圖像上的鄰居patch塊。。

步驟(4)，采用局部線性結構保持算法學習對應關系的權重：對于任意patch塊i，根據步驟(3)中構建的對應關系有向圖找到其鄰居patch塊集合，記為由局部線性保持原理得：

上式中，P是所有patch塊數，表示patch塊i的sift特征，w_ij為學習到的權重系數。w_ij的求解采用經典的局部線性嵌入(local linear embedding)算法中的構造協方差矩陣及拉格朗日乘子法進行求解。

步驟(5)，通過迭代求解算法在對應局部區域之間傳遞其前背景分割結果，得到最終分割結果：包括最小優化方程的構造和優化算法兩個主要步驟。

第一步，根據步驟(3)得到的patch塊對應關系圖和步驟(4)學習到的對應關系權重系數，構造如下最小優化方程式：

上式中，y表示輸入的M幅圖像的前背景分割結果，y^[i]表示第i幅圖像的前背景分割結果，表示第i個patch塊的前背景分割結果，E_seg是經典的馬爾科夫能量項，表示圖像內部的像素點之間的關系，α為系數。

第二步，采用半二次方分裂(half-quadratic splitting)最小化方法迭代求解已構造的最小優化方程式：首先，引入輔助變量z，同時假設在任意patch塊上都滿足將該限制條件引入到第一步構造的方程式中得到如下優化方程式：

上式中，α和λ為系數，w_ij表示patchi和patchj之間的權重值。

接下來，通過固定其中一個變量求解另一個變量的方法，將上式分解為兩個簡單的子問題，如下所示：

對于第一個子問題：將第二項并入到MRF能量項的一次項中，并通過經典的圖割算法進行優化；對于第二個子問題：通過求導的方式求解最優的解。通過不斷的迭代求解y和z，將達到終止條件或最大迭代次數的y作為分割最終結果。

本發明與現有技術相比的優點在于：本發明提出的局部形狀遷移指導的圖像對象共分割方法，框架簡單且易于實現，執行時空效率高，解決了對象全局形狀不一致時分割效果不好的問題，其中，采用局部線性嵌入方法學習得到權重，為局部形狀遷移提供更加魯棒的保證。

附圖說明

圖1是本發明的流程圖；

圖2是本發明在公開數據集上的測試結果圖。

具體實施方式

如圖1所示，本發明提出了局部形狀遷移指導的圖像對象共分割方法，包括以下步驟：

(1)圖像集預處理：輸入M幅包含相同語義類別對象的圖像，使用Zhang等人在2015年提出的顯著性檢測方法對每幅圖像進行顯著性分析，將顯著性檢測結果使用二倍均值做閾值得到mask圖，即為前背景初始分割結果，其中mask圖僅由0和1組成，1代表前景像素點，0代表背景像素點。

(2)對任意兩幅圖片進行稠密特征點匹配：針對每一幅圖像i(i＝1,2,…,M)，為圖像上每一個像素點生成128維的dense sift特征；將每一幅圖片i(i＝1,2,…,M)的dense sift特征與其他圖片j(j＝1,2,…,M且j≠i)的dense sift特征采用Kim等人在2013年提出的可變形的空間金字塔匹配算法(DSP)進行稠密特征點匹配，得到稠密特征點的水平位移h_ij和垂直位移v_ij。

(3)根據匹配結果，建立每一局部圖像區域與來自其他圖像的局部區域之間的對應關系：對每一幅圖像i，每間隔5個像素點選取一個17*17的patch塊，用中心像素點坐標表示該patch塊的位置，用中心像素點的sift特征描述子表示該patch塊的特征；使用步驟(2)中得到的水平位移h_ij和垂直位移v_ij，計算出每一個patch塊在其他圖像上與之對應的patch塊的位置；構建patch塊的對應關系有向圖，頂點代表patch塊，有向邊指向該patch塊在其他圖像上的鄰居patch塊。

(4)采用局部線性結構保持算法學習對應關系的權重：對于任意patch塊i，根據步驟(3)中構建的對應關系有向圖找到其鄰居patch塊集合，記為由局部線性保持原理得：

上式中，P是所有patch塊數，表示patch塊i的sift特征，w_ij為學習到的權重系數。w_ij的求解采用經典的局部線性嵌入(local linear embedding)算法中的構造協方差矩陣及拉格朗日乘子法進行求解。

(5)通過迭代求解算法在對應局部區域之間傳遞其前背景分割結果，得到最終分割結果：包括最小優化方程的構造和優化算法兩個主要步驟。

第一步，根據步驟(3)得到的patch塊對應關系圖和步驟(4)學習到的對應關系權重系數，構造如下最小優化方程式：

上式中，y表示輸入的M幅圖像的前背景分割結果，y^[i]表示第i幅圖像的前背景分割結果，表示第i個patch塊的前背景分割結果，E_seg是經典的馬爾科夫能量項，表示圖像內部的像素點之間的關系，α為系數。

第二步，采用半二次方分裂(half-quadratic splitting)最小化方法迭代求解已構造的最小優化方程式：首先，引入輔助變量z，同時假設在每一patch塊上都滿足將該限制條件引入到第一步構造的方程式中得到如下優化方程式：

上式中，α和λ為系數，在本實驗中設置為α＝1，λ＝0.3；w_ij表示patchi和patchj之間的權重值。

接下來，通過固定其中一個變量求解另一個變量的方法，將上式分解為兩個簡單的子問題，如下所示：

對于第一個子問題：將第二項并入到MRF能量項的一次項中，并通過經典的圖割算法進行優化；對于第二個子問題：對求導，得到下式：

將上式轉化為矩陣形式如下：

Z'＝{λY+α[W+W^T-W^TW+Diag(W^TW)]Z}[(α+λ)I+Diag(W^TW)]^-1，

上式中，矩陣Z,Z',Y分別由列向量連接而成；W是大小為P*P的矩陣，其數值代表patch塊之間的權重；I是單位矩陣；Diag(·)運算實現創建對角矩陣，其非零元素為輸入矩陣對角線上的元素。

通過對上式進行不斷迭代求解得到Z，實驗中設置迭代次數為15，每次迭代中都將Z歸一化到[0,1]之間。

最后，將最大迭代次數設置為10，使用y在兩次迭代結果之間的差異不超過M幅圖像像素點總數的0.0001倍作為迭代終止條件，通過不斷的迭代求解兩個子問題中的y和z，并將達到迭代終止條件或者達到最大迭代次數的y作為最終分割結果。圖2所示為部分共分割結果，即(a)(b)(c)(d)四組，每組中上方為原始圖像，下方對應共分割結果。