一種基于幅頻特征稀疏濾波的圖像分類方法與流程

本發明涉及的是一種圖像分類的方法，具體可以應用到各種需要圖像分類的場景中。

背景技術：

稀疏濾波技術，是指通過約束信號重構系數矢量中非零系數的個數，達到優化特征表達，提高計算速度的效果，此外，稀疏濾波可以對信號產生壓縮效果，以此節約存儲和傳輸空間。

稀疏濾波應用到圖像分類中，就是用圖像信號的稀疏特征系數代替圖像本身作為分類的信號樣本。對于基于稀疏濾波的圖像分類技術來說，常用做法是采用矩陣分解技術，通過將原始圖像像素矩陣X分解為兩個矩陣U和A的乘積，其中，矩陣U為基矩陣，控制圖像特征由高維向低維轉化，矩陣A為稀疏系數矩陣，其中每一列系數矢量中，存在極少數的非零元素，訓練稀疏模型時，采用L-1范數約束稀疏系數矩陣A的稀疏度，分類時，使用圖像信號的稀疏系數矩陣作為分類器的輸入，分類圖像。這種方式的缺點在于：一，對矩陣A做L-1范數稀疏度約束，容易使學習到的模型產生過擬合，影響分類的效果，甚至，嚴重時會產生錯誤分類，在分類結果與安全因素相關時，會導致嚴重的安全災難；二，如果對矩陣U做過擬合懲罰，則增加了優化項，使優化過程復雜化，需要昂貴的計算資源。

圖像的幅頻特征，是指將圖像信號或者可以代表圖像信號的特征信號作為二維信號進行調和分析，使用諸如離散傅里葉變換，Z變換，小波變換，希爾伯特-黃變換等手段，獲取到的圖像數據在頻率域的特征，是信號幅度與信號頻率之間的關系。利用圖像的幅頻特征進行稀疏濾波，可以在利用圖像信號的頻率特性建立濾波模型，避免直接對矩陣A和矩陣U做約束，從而有效地避免了過擬合和優化過程的復雜化。

技術實現要素：

本發明提供一種基于幅頻特征稀疏濾波的圖像分類技術，利用圖像信號的幅頻特征建立稀疏濾波模型；利用稀疏特征矩陣進行圖像分類。

本發明技術方案為：

一種基于幅頻特征稀疏濾波的圖像分類方法，包括以下步驟：

1)訓練數據獲取階段，獲取待分類圖像數據的一個子集，格式化為統一維度的圖像數據矩陣X；

2)初始化階段，生成兩個隨機矩陣，分別為維度為f*n的基矩陣U，維度為n*m的稀疏系數矩陣A；

3)變換階段，對矩陣A或圖像數據矩陣X進行調和變換，獲得幅頻特征矩陣F；

4)優化建立階段，通過約束原始矩陣X與重構矩陣Y＝UA的能量差最小，以及幅頻特征矩陣F的能量最大，選取一種優化算法，執行迭代優化，例如，可以選取梯度下降算法；

5)優化迭代階段，重復執行4，直到目標函數值達到預期的目標或者迭代次數達到預先設定的最大值；

6)生成階段，用基矩陣U和新的待分類圖像矩陣Z，生成矩陣Z的稀疏系數矩陣B；

7)分類階段，選擇一種分類器，矩陣B作為分類器輸入，獲取分類結果。

本發明的有益效果為：一種基于幅頻特征稀疏濾波的圖像分類技術具有非常廣泛和實用的應用場景，比如，在生產環境中，由于傳感器采集到的圖像數據都是帶有隨機噪聲和自然背景的圖像數據，這些數據會放大L-1范數稀疏度約束的過擬合效果，嚴重干擾圖像分類結果。基于幅頻特征的稀疏濾波方法，通過在頻域建立稀疏濾波模型，有效避免了直接約束稀疏系數矩陣帶來的過擬合問題，并且通過減少優化項，提高了優化效率，不但節省了計算資源，而且提高了分類器的分類精度，因此，具有廣闊的應用前景。

附圖說明

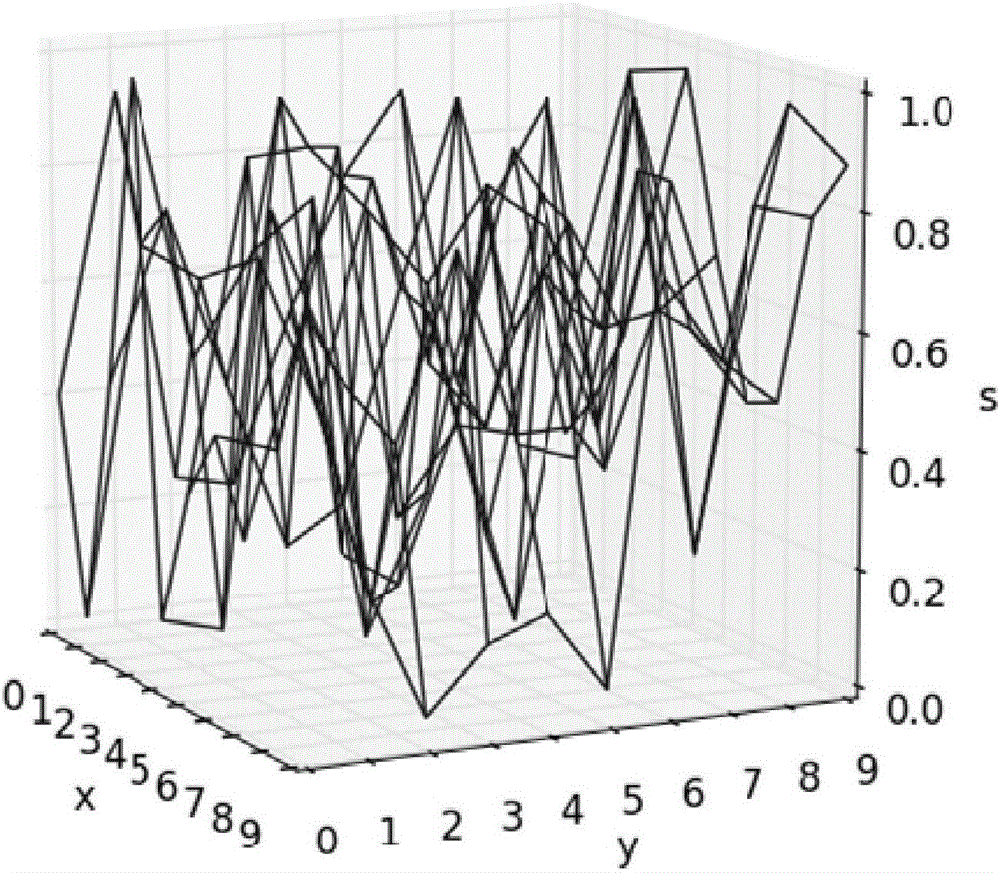
圖1(a)為稀疏度為α的矩陣A的圖像；

圖1(b)為圖1(a)中矩陣A的幅頻特征矩陣F的圖像；

圖2(a)為稀疏度為β的矩陣A的圖像；

圖2(b)為圖2(a)中矩陣A的幅頻特征矩陣F的圖像

圖3(a)為稀疏度為γ的矩陣A的圖像；

圖3(b)為圖3(a)中矩陣A的幅頻特征矩陣F的圖像

圖中：x，y分別為矩陣A兩個維度坐標；s代表矩陣A的二維信號函數值；u，v分別為矩陣F的兩個維度坐標；稀疏度α<β<γ。

具體實施方式

下面結合附圖和技術方案詳細說明本發明。

第一步，訓練數據獲取階段

獲取待分類圖像數據之后，選取一個子集作為訓練數據，格式化為m*(w*h)維度的圖像數據矩陣X；其中，m為樣本數目，w、h為單個圖像的長、寬；設f＝w*h為圖像原始特征空間維度，即待分類圖像中像素點的個數；

第二步，初始化階段

設置稀疏特征數目為n(n<f)，隨機生成元素數值在0～1之間的兩個二維矩陣，分別為維度為f*n的基矩陣U和維度為n*m的稀疏系數矩陣A；

第三步，變換階段

對稀疏系數矩陣A或者圖像數據矩陣X進行調和變換，獲得幅頻特征矩陣F；所述的調和變換的方法包括離散傅里葉變換、快速傅里葉變換、離散余弦變換、Z變換、小波變換或希爾伯特-黃變換等；

假設采用稀疏系數矩陣A執行離散傅里葉變換，用s(x,y)代表A的二維信號函數，F(u,v)代表s(x,y)的幅頻特征，則：

其中，u,v代表F的兩個維度坐標，x,y代表A兩個維度坐標，m為樣本數目，n為稀疏特征數目。

第四步，優化建立階段

將幅頻特征矩陣F的協方差矩陣的和的L-2范數的相反數作為F的能量，記為E(F)；設幅頻特征矩陣F的第i個列向量的協方差矩陣為R(F_i)，則稀疏度約束函數spi＝λ||X-UA||₂+E(F)。其中，λ為能量約束系數，一般取0.5；重構矩陣Y＝UA為基矩陣U和稀疏系數矩陣A的乘積；i、j分別表示幅頻特征矩陣F的維度坐標。

第五步，優化迭代階段

以稀疏度約束函數為目標函數，根據約束目標函數中圖像數據矩陣X(原始矩陣)與重構矩陣Y的能量差最小，以及幅頻特征矩陣F的能量最大，選取梯度下降算法，執行迭代優化。

所述的梯度下降算法具體為：

目標函數spi對稀疏系數矩陣A，基矩陣U的梯度更新矩陣函數分別為：

G_spi/U＝-XA^T+(UA)A^T

設置迭代次數，通過以上兩個梯度更新矩陣，執行以spi函數為目標函數的迭代優化，至目標函數值達到預期的目標或者迭代次數達到預先設定的最大值，梯度下降算法結束。

附圖是對迭代優化過程中，幅頻特征矩陣與稀疏系數矩陣變化趨勢的說明，圖1(a)、圖2(a)、圖3(a)為稀疏度遞增的稀疏系數矩陣A的圖像；圖1(b)、圖2(b)、圖3(b)分別為圖1(a)、圖2(a)、圖3(a)中矩陣A的幅頻特征矩陣F的圖像；隨著圖1(b)、圖2(b)、圖3(b)中幅度偏離中心程度的逐漸變大，相應地，圖1(a)，圖2(a)，圖3(a)的稀疏度逐漸變大。

第六步，生成階段

設新的待分類圖像數據矩陣為Z，由第五步得到的基矩陣U和待分類圖像數據矩陣Z生成矩陣Z的稀疏系數矩陣B，即B＝U^-1Z。

第七步，分類階段

將稀疏系數矩陣B作為分類器的輸入矩陣，執行分類。