微處理器及其方法與流程

相關申請

本申請主張申請日為2014年7月2日的美國專利第62/020,246號臨時申請“Non-Atomic Split-Path Fused Multiply-Accumulate with Rounding cache”與申請日為2015年6月10日的美國專利第62/173,808號臨時申請“Non-Atomic Temporally-Split Fused Multiply-Accumulate Apparatus and Operation Using a Calculation Control Indicator Cache and Providing a Split-Path Heuristic for Performing a Fused FMA Operation and Generating a Standard Format Intermediate Result”的優先權。該些優先權案的全文并入本申請以供參考。

本申請還關聯于下列與本申請同時申請的申請：標題為“Temporally Split Fused Multiply-Accumulate Operation”的美國第14/748,870號申請；標題為“Calculation Control Indicator Cache”的美國第14/748,924號申請；標題為“Calculation Control Indicator Cache”的美國第14/748,956號申請；標題為“Standard Format Intermediate Result”的美國第14/749,002號申請；標題為“Split-Path Heuristic for Performing a Fused FMA Operation”的美國第14/749,050號申請；標題為“Subdivision of a Fused Compound Arithmetic Operation”的美國第14/749,088號申請；與標題為“Non-Atomic Split-Path Fused Multiply-Accumulate”的美國第14/748,817號申請。這些申請的全文并入本申請以供參考。

技術領域

本發明有關于一種執行算術運算的微處理器設計，尤其是融合浮點乘積-累加(FMA)運算的微處理器設計。

背景技術：

在現代計算機設計中，從大約1990年起，融合浮點乘積-累加(floating-point multiply-accumulate,FMA)運算就已經成為一個受到商業矚目與學術關注的領域。融合FMA運算是一種算術運算，其形式為±A*B±C，其中，A、B與C是浮點輸入運算元(分別是一個被乘數(multiplicand)、一個乘數(multiplier)、與一個累加數(accumulator))，并且在C累加至A與B的乘積前不存在舍入(rounding)運算。±A*B±C可包含，但不限于，下列例子：(a)A*B+C；(b)A*B–C；(c)–A*B+C；(d)–A*B–C；(e)A*B(即C設為零)；與(f)A+C(即B設為1.0)。

在大約1990年，此算術運算即以一原子(atomic)或不可分割(inseparable)運算的形式商業實現于IBM的精簡指令集(RISC)系統/6000。而后續設計進一步最佳化浮點乘積累加運算。

在其2004年的文獻“Floating-Point Multiply-Add-Fused with Reduced Latency”中，Tomas Lang與Javier D.Bruguera(“Lang et al.”)提出與最佳化FMA設計有關的許多重要課題。這些課題包括，指數差值與累加器移位/對準量的預計算，累加器與相乘陣列的平行對準，必要時使用2’補數累加器(2’s complement accumulator)，和向量與進位向量的條件反轉，在最終相加/舍入模組前對于和向量與進位向量的標準化處理，LZA/LOA與標準化移位的重迭運算，進位位、舍入位、保護位與粘(sticky)位的分別運算，以及在合一的相加/舍入模組中具有1m寬度的雙總和加法器的使用(其中，m是其中一個運算元的尾數(mantissa)寬度)。

在其2005年的文獻“Floating-Point Fused Multiply-Add:Reduced Latency for Floating-Point Addition”中，Tomas Lang與Javier D.Bruguera(“Lang et al.”)提出利用分離數據路徑(或雙數據路徑)把對準方向從標準化的情況移開，其中，“近(close)”的數據路徑是用以從{2,1,0,-1}有效減去指數差值(此概念在本申請詳細說明中會有更進一步的發展與改進)，而“遠(far)”的數據路徑則是用來處理其他情況。Lang等人還提出在遠的數據路徑使用雙對準平移器來處理相乘陣列的進位儲存輸出，以及在近的數據路徑使用非常有限對準平移的方法。

在2004年的文獻“Multiple Path IEEE Floating-Point Fused Multiply-Add”中，Peter-Michael Seidel(“Seidel”)提出對于FMA設計的不同改進方法，即使用多個平行運算路徑。Seidel并提出關閉未使用的路徑門；從指數差值與有效運算確認多個運算路徑；使用兩個不同運算路徑，其中一個提供給容易產生塊消去(mass cancellation)的小指數差值使用，另一個則是用來處理其他情況；對于具有效減法的小指數差值的情況，在有效乘積運算中插入累加器數值。

在現今隨處可見個人行動運算裝置來提供擴充媒體分發與網路內容存取的情況下，更需要去設計一個的低制作成本、少功耗，但又能以高效能執行指令的FMA邏輯電路。

執行FMA運算的主要方法涉及合一的乘積-累加單元的使用，以執行整個FMA運算，包含對結果進行舍入。大部分學術提案與商業應用都描述一個單塊的，或是不可分割的功能方塊，其具有將兩個數相乘，將未進行舍入的乘積與一第三運算元、加數或累加器進行相加操作、以及對運算結果進行舍入運算。

另一種替代方案使用傳統的乘法單元來執行A*B的子運算，然后使用傳統的加法單元來將A與B的乘積與C相加。不過，此傳統分工處理的方法會犧牲運算速度以及在同一個單元內將C與A和B的部分乘積累加運算所能得到的效能增益。傳統分工處理的方法也涉及兩個舍入運算，因A與B的乘積會進行舍入運算，而后續C與乘積的加總也會進行舍入運算。因此，相較于合一處理的方法，傳統分工處理的方法有時候會產生不同且較不準確的結果。同樣地，因為重復舍入運算的存在，此傳統分工處理的方法無法執行“融合(fused)”FMA運算，而未能符合IEEE 754技術標準關于浮點運算的要求。

因為FMA硬件可同時用于多個運算目的并遵從IEEE 754技術標準，在現代的產品中，計算機設計者往往會選擇利用不可分割的FMA執行單元來完全取代傳統分離的乘積與加法功能方塊。然而，此方法會帶來許多不利影響。

第一，相較于使用獨立的加法與乘法功能單元，FMA硬件的設置成本較高，也較復雜。第二，在執行簡單的加法或乘法運算時，相較于使用獨立的加法與乘法功能單元，使用FMA硬件的延遲較長，且通常會消耗較多能量。第三，對于超純量(superscalar)計算機設計而言，將乘法與加法的功能合并于單一個功能方塊會減少算術指令可發送端口的數量，而削減計算機針對源碼、機械層級或軟體開發平行處理的能力。

前述第三個不利影響可加入更多功能單元來處理，例如一個獨立的加法功能單元，但這會增加設置成本。基本上，一個額外的加法器(舉例)就是為了在提供不可分割的FMA功能時，維持可接受的指令層級平行處理所需付出的代價，這又會增加整個硬件的設置尺寸，并會增加寄生電容與電阻。隨著半導體制造技術朝向小尺寸發展，寄生電容與電阻會對于算術運算的時間延遲，或稱延遲(latency)，有更顯著的影響。此時間延遲有時會被模擬為因為“長導線”而造成的延遲。因此，為了減少實行不可分割的FMA運算對于指令層級平行處理影響所額外設置的功能方塊，在考量所需的晶片尺寸、功耗與算術運算的延遲后，所能提供的改善其實相當有限。

因此，最佳的提案與實施通常會(但不總是)提供正確的運算結果(對應于IEEE的舍入與其他說明)，有時提供較高的指令產出(throughput)，但顯然需要額外的硬件電路而增加設置成本，并且會需要增加功耗來在復雜的FMA硬件上執行簡單的乘法與加法運算。

現代FMA設計所要達成的目標仍未能完全達成。

技術實現要素：

本發明的一方面，提供一種微處理器中的方法，用以執行一±A*B±C形式的融合乘積-相加運算，其中A、B與C為輸入運算元；該方法先是進行一評估，測試A、B與C的值是否符合一充分條件，以執行一具有A與B部分乘積的C的聯合相加運算；若為是，則以A與B的部分乘積進行C的聯合相加運算，且其聯合相加運算的結果再進行舍入運算；若為非，則進行A與B部分乘積的一基本相加運算，借此，產生基本相加運算一未舍入非冗余結果，此未舍入結果再去尾數，以產生一排除一或多個最不顯著位的未舍入非冗余中間結果向量；接著，再執行一次要相加運算，將C加或減至未舍入非冗余中間結果向量中；最后，次要相加運算的結果即進行舍入運算。

依據本發明的一實施例，去尾數足以產生一未舍入非冗余中間結果向量，其尾數寬度相等于一用于融合乘積-相加運算的目標數據格式的尾數寬度。

依據本發明的一實施例，假使A、B與/或C符合一充分條件、以執行一具有A與B部分乘積的C的聯合相加運算，則ExpDelta用以對準一具有A與B部分乘積尾數的C。

依據本發明的一實施例，假若A、B與/或C不符合一用以執行一具有A與B部分乘積的C的聯合相加運算的充分條件，則被排除的最不重要位被減低至一組一或多個舍入指標，此舍入指標稍后使用在次要相加運算的結果的舍入運算上。

在本發明的另一方面，提供一種微處理器，其包括：可操作以執行一±A*B±C形式的融合乘積-相加運算的一或多個指令執行單元，其中A、B與C為輸入運算元；一或多個指令執行單元中提供運算元分析邏輯，用以指明A、B與C的值是否符合一充分條件，以執行一具有A與B部分乘積的C的聯合相加運算。而且，亦提供控制邏輯，假使符合一充分條件，指引一或多個指令執行單元去執行一具有A與B部分乘積的C的聯合相加運算，以及此聯合相加運算的一結果的舍入運算。假使未符合任何充分條件，此控制邏輯則指引一或多個指令執行單元去進行一A與B部分乘積基本相加運算，以產生基本相加運算的一未舍入結果，將未舍入結果去尾數，以產生一排除一或多個最不重要位的未舍入中間結果向量，未舍入結果，執行一C的次要相加運算至未舍入中間結果向量，并進行次要相加運算一結果的舍入運算。

依據本發明的一實施例，假若A、B與/或C不符合一用以執行一具有A與B部分乘積的C的聯合相加運算的充分條件，則控制邏輯即指引一或多個指令執行單元去減低被排除的一或多個最不顯著位至一組使用于次要相加運算結果舍入運算的一或多個舍入指標。再者，控制邏輯亦指引從被排除的一或多個最不重要位，使用于次要相加運算結果舍入運算，產生一或多個舍入指標。

依據本發明的一實施例，微處理器亦包括一用以儲存未舍入中間結果向量的第一共享指令執行單元儲存空間、以及一用以儲存多個舍入指標的第二共享指令執行單元儲存空間。

在本發明的另一方面，微處理器中的方法用以執行一±A*B±C形式的融合乘積-相加運算，其中A、B與C為輸入運算元。此方法包括偵測A、B與C的值是否符合一充分條件、以執行一具有A與B部分乘積的C的聯合相加運算。若為是，則進行具有A與B部分乘積的C的一聯合相加運算，接著進行聯合相加運算一結果的舍入運算；若為非，則進行A與B部分乘積的基本相加運算、以產生一未舍入中間結果向量與一或多個舍入指標，用于基本相加運算中，之后，進行C的次要相加運算至未舍入中間結果向量中，接著再使用一或多個舍入指標去執行此次要相加運算一結果的舍入運算。

依據本發明的一實施例，如果一A與B乘積的絕對值實質上大于C的絕對值，則存在有用以執行一具有A與B部分乘積的C的聯合相加運算的充分條件。

依據本發明的一實施例，此方法還包括、通過計算一指數差ExpDelta、去評估一A與B乘積的絕對值是否實質上大于C的絕對值，此指數差ExpDelta為一A與B指數值的總和減去C的指數值的函數。指數差ExpDelta亦可從A與B指數值的總和減去C的指數值上再減去一指數偏移值；例如，當ExpDelta>＝-2時，則用以執行一具有A與B部分乘積的C的聯合相加運算的充分條件是存在的。

在本發明的另一方面，提供一微處理器，乃包括可操作以執行一±A*B±C形式的融合乘積-相加運算的一或多個指令執行單元，其中A、B與C為輸入運算元；一或多個指令執行單元中提供運算元分析邏輯、用以指明A、B與C的值是否符合一充分條件、以執行一具有A與B部分乘積的C的聯合相加運算。而且，亦提供控制邏輯，假使符合一充分條件，指引一或多個指令執行單元去執行一具有A與B部分乘積的C的聯合相加運算、以及此聯合相加運算的一結果的舍入運算。假使未符合任何充分條件，此控制邏輯則指引一或多個指令執行單元去進行一A與B部分乘積基本相加運算、以產生基本相加運算的一未舍入結果，之后，再執行一C的次要相加運算至未舍入中間結果向量，且最后使用一或多個舍入指標舍入次要相加運算的一結果。

依據本發明的一實施例，未舍入中間結果向量具有與用于融合乘積-相加運算一目標數據格式的一尾數寬度相同的尾數寬度。

依據本發明的一實施例，一用以執行一具有A與B部分乘積的C的聯合相加運算的充分條件為在執行融合乘積-相加運算中的一潛在性塊消法用戶，此塊消法可定義為A與B乘積的一或多個最重要位的求反運算與相加數C加總。

在本發明的另一實施例中，一用以執行一具有A與B部分乘積的C的聯合相加運算的充分條件為融合乘積-相加運算可產生一有效減法的狀態，其中一有效減法指明當將C及A與B乘積的相加或相減會產生一結果R，其具有一絕對值、乃小于(a)A與B乘積的絕對值、或(b)C的絕對值中的較大者；且A與B指數值的總和減去C的指數值落到X至Y的范圍中(減去任何指數偏移值)，例如，X可為-2、且Y可為+1。

此方法與裝置可縮減所需的電路、設置成本與復合算術運算的累增功耗。簡單來說，此裝置與方法是將復合算數運算分成至少二個子運算，由物理上與/或邏輯上各自獨立的硬件單元來執行。每個硬件單元執行此復合算術運算的一部分。舍入運算或運算控制所需的位于此二運算間，儲存于一快取內。這些子運算于不同時間與位置完成，而必要的數據片段會被整合以完成最終舍入運算。

此方法與裝置具有許多值得注意的優點，尤其是針對FMA運算。

第一，此方法與裝置可辨識FMA運算并將其區分為至少二種類型，其中部分運算以暫時或物理性分割的方式執行。

第二，此方法與裝置可將來自指令集架構(ISA)的一不可分割的(atomic)或一體的(unified)FMA指令轉譯或轉換為至少二個子運算。

第三，此方法與裝置容許這些子運算以非不可分割的、或暫時物理性分割的方式來執行，例如在非循序超純量計算機處理器裝置內執行。

第四，FMA運算(例如對應于部分第一類型的FMA運算或部分第二類型的FMA運算)中部分的必須算術運算于執行第一特定微指令時執行。

第五，此方法與裝置以一新的方式預先計算FMA的符號數據。

第六，此方法與裝置會儲存中間運算的部分結果，例如儲存于一結果(重命名)暫存器。

第七，此方法與裝置會儲存運算結果的其他部分，例如儲存至稱為舍入快取或運算控制指標快取的其他儲存單元。

第八，此方法與裝置會將所收集到的數據，即中間結果，以新的標準化儲存格式來儲存。此外，此方法與裝置可能會將儲存格式中間結果轉送至后續特殊類型的第二微指令，而非進行儲存。

第九，此方法與裝置在需要提供所儲存的數據至后續第二微指令時，會存取舍入快取。

第十，響應來自舍入快取的數據，此方法與裝置會選擇性地提供FMA加數至第二微指令或使輸入值歸零。

第十一，此方法與裝置會在執行一第二(或更多)微指令的過程中，使用此儲存格式中間結果作為輸入，來執行第一類型或第二類型的FMA運算中剩下必須執行的算術FMA運算。

第十二，此方法與裝置將經少量調整的現有技術乘法硬件執行單元與加法硬件執行單元結合，如結合所述的舍入快取與數據轉送網路用以回避舍入快取。

第十三，此方法與裝置不會讓分配端口無法于算術運算中使用、或是在計算機利用指令平行處理的能力與投資的硬件成本間妥協。

本發明所采用的具體實施例，將通過以下的實施例及圖式作進一步的說明。

附圖說明

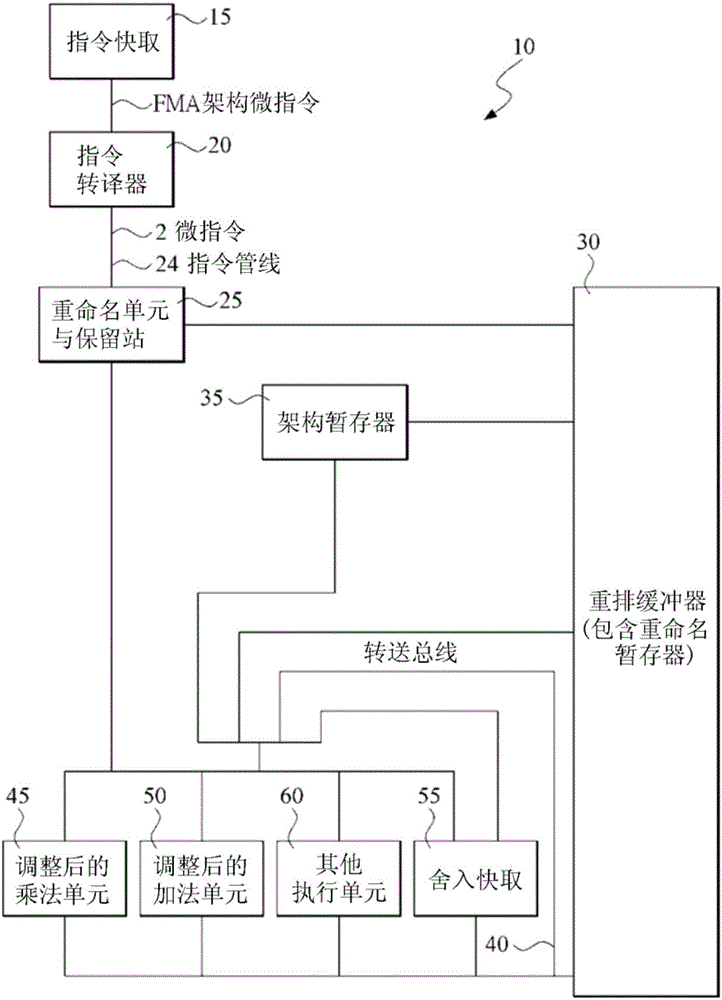
圖1是一微處理器的方塊示意圖，此微處理器具有執行單元與一舍入或運算控制指標快取，并使用二個子運算、一個調整后的乘法器與一個調整后的加法器來執行FMA運算。

圖2是一示意圖，將一數字空間區分為FMA運算的五個類型以為例示(但非限定于此)。

圖3是一功能方塊圖，描述用以執行FMA運算的調整后的乘法器與調整后的加法器內的邏輯元件。

圖4是一功能方塊圖，顯示本發明一實施例的乘法運算單元的路徑確認邏輯與尾數乘法模組，此乘法運算單元經適當調整以接收FMA乘數、被乘數與累加數作為輸入運算元。

圖5是一功能方塊圖，顯示圖4的乘法運算單元的指數結果產生器與舍入指標產生器，此乘法運算單元經適當調整以產生一儲存格式中間結果。

圖6是一功能方塊圖，顯示經適當調整以接收一儲存格式中間結果與累加數的加法運算單元的一實施例。

圖7是一功能方塊圖，顯示非不可分割的分路FMA運算的一實施例的第一FMA子運算中的一路徑確認部分。

圖8是一功能方塊圖，顯示非不可分割的分路FMA運算的第一FMA子運算中的一乘法與累加部分。

圖9A及圖9B是以一功能方塊圖，顯示非不可分割的分路FMA運算的第一FMA子運算中的一儲存格式中間結果產生部分。

圖10是一功能方塊圖，顯示非不可分割的分路FMA運算的第二FMA子運算。

圖11是一示意圖，顯示將融合FMA指令轉譯為第一與第二FMA微指令的一實施例。

具體實施方式

微處理器

圖1是一微處理器的方塊示意圖。此微處理器10具有多個執行單元45,50,60用以執行FMA運算。此微處理器10包含一指令快取15，一指令轉譯器與/或微碼只讀存儲器20，一重命名單元與保留站25，多個執行單元(包含一調整后的乘法器45、一調整后的加法器50與其他執行單元60)，一舍入快取55(或是指運算控制指示器儲存空間)，架構暫存器35與一重排緩沖器30(包含重命名暫存器)。其他的功能單元(未圖示)可包含一微碼單元；分支預測器；一存儲器子系統，其包含一快取存儲器階層架構(例如階層一的數據快取、階層二的快取)、存儲器排列緩沖器、與存儲器管理單元；數據預擷取單元；與一總線接口單元等等。微處理器10具有一非循序執行微架構，可以不依照程序順序發布指令以供執行。進一步來說，架構指令(或微指令)轉譯或轉換出的微指令，可以不依照程序順序發布指令以供執行。微指令的程序順序相同于轉譯或轉換出這些微指令的相對應架構指令的程序順序。微處理器10并具有一超純量微架構，其能在單一個時鐘周期內發布多個指令至執行單元執行。在一種實施例中，微處理器10可以說是以相容于x86指令集架構的方式提供指令以供執行。

指令快取15儲存由系統存儲器擷取的架構指令。指令轉譯器與/或微碼只讀存儲器20將由系統存儲器擷取的架構指令轉譯或轉換為微處理器10的微架構微指令集的微指令。執行單元45,50,60執行這些微指令。這些由架構指令轉譯或轉換出的微指令可實現架構指令。重命名單元25接收微指令并將重排緩沖器的項目依據程序順序分配給微指令、依據所分配的重排緩沖器項目索引更新這些微指令、將各個微指令發送至與將要執行這些微指令的執行單元相關聯的保留站25、以及為這些微指令執行暫存器重命名與關聯建立。

基于類型的分類運算

在本發明的一實施例中，FMA運算是依據輸入運算元的指數值的差(由變數ExpDelta表示)，以及是否涉及一有效的減法運算來進行分類。圖2利用一包含有數字線70的數字空間65來顯示ExpDelta的值。在數字線70下方的空間顯示此運算會構成一有效減法運算。在數字線70上方的空間顯示此運算會構成一有效加法運算(亦即不存在有效減法運算)。

指數差，表示為ExpDelta，是乘數與被乘數的輸入指數值的加總，減去任何指數偏移值，再減去加數或減數的輸入指數值。在累加值遠大于偏移調整乘積向量(bias-adjusted product vector)時，計算出的ExpDelta為負。而在累加值遠小于偏移調整乘積向量時，計算出的ExpDelat為正。

“有效減法”，由變數EffSub表示，是指輸入運算元的符號與所欲執行的運算(例如乘法－加法，或是乘法－減法)的結合，將會有效降低浮點數結果的大小，而非增加。舉例來說，負的被乘數乘上正的乘數(乘積為負)后，加上一個正的加數，就會有效降低結果的大小，而會表示為有效減法(EffSub)。

如圖2的數字空間65的右側所示，在乘積向量的大小主導運算結果的情況下，累加數會直接用于初始舍入位(round bits)或是粘位(sticky bits)的運算。如本文后續將描述的，累加數與乘積尾數的相對對準有利于在計算影響舍入運算的位前將此二者相加。在圖2的數字空間65內，這些不存在“有效減法”的情況顯示為“類型2”運算80，而存在“有效減法”的情況顯示為“類型4”運算90。

如圖2的數字空間65的左側所示，在累加數的大小主導運算結果，并且累加數的尾數大小小于或等于所欲產生結果的尾數大小，累加數就不會用于初始舍入位或是粘位的運算。在圖2的數字空間65內，這些不存在“有效減法”的情況顯示為“類型3”運算85，而存在“有效減法”的情況顯示為“類型5”運算95。因為累加數有效對準乘積尾數的左側，所以可獲得在加上累加數之前，先確認粘位與舍入位的好處。

區分出ExpDelta位于圖2的數字線70的右側的情況與ExpDelta位于圖2的數字線70的左側的情況會有許多優點。舉例來說，傳統FMA利用非常寬的對準移位器－相當于或大于輸入尾數寬度的三倍－來解釋累加數對準于乘數與被乘數的乘積的左側或右側的運算。通過將FMA運算區分為由兩個調整后的執行單元(一個調整后的乘法器45與一個調整后的加法器50)分別執行的兩個子運算，即可利用較小的數據路徑與較小的對準移位器來進行運算。

對于數字線70的右側的運算，累加數的大小會小于中間乘積向量，此情況有利于在調整后的乘法器45內將累加數與乘法器的乘積相加。此運算只需要一個比傳統FMA的數據路徑的寬度還要小上大約一個尾數寬度的數據路徑。因為調整后的乘法器45原本就具有一些內部延遲，累加數會有效地對準加總樹/陣列(summation tree/array)，也會簡化標準化與舍入運算。舍入運算將會由調整后的加法器50會在第二FMA子運算中執行。

反之，對于數字線70的左側的運算，累加數會是較大的運算元而不會用于舍入運算。因為累加數不會用于舍入運算(除了以下提到的特殊狀況)，因而可以對乘法器的乘積執行一些初始粘收集(initial sticky collection)、將中間結果儲存至存儲器(例如重排緩沖器與/或快取)、并且可以用調整后的加法器50來進行累加數的加法運算。傳統的舍入邏輯可有效處理累加數對舍入運算的選擇造成影響的特殊狀況，若是存在總數溢位，舍入位會成為粘位的其中之一，而總數的最重要位(least significant bit,LSB)會成為舍入位。

某些種類的FMA運算－“有效減法”運算中對應于在圖2的數字空間65下半部的子集合－會使一個或多個最重要位歸零，傳統上將此稱為“塊消去(mass cancellation)”。在圖2中，具有塊消去潛力的運算表示為“類型1”運算75。此情況需要在舍入運算前執行標準化運算來確認舍入點的位置。標準化向量所涉及的移位運算會產生顯著的時間延遲與/或呼叫前導位預測(leading digit prediction)以供使用。另一方面，不涉及塊消去的FMA運算可以省略前導位預測。

總之，如圖2所示，FMA運算可依據ExpDelta與EffSub進行分類。第一類的FMA運算75定義為包含ExpDelta落于{-2,-1,0,+1}的范圍且EffSub為真的運算，這些運算包含那些具有位塊消去潛力的運算。第二類的FMA運算80是定義為包含ExpDelta大于或等于-1且EffSub為假的運算。第三類的FMA運算85是定義為包含ExpDelta小于或等于-2且EffSub為假的運算。第四類的FMA運算90是定義為包含ExpDelta大于{+1}且EffSub為真的運算。第五類的FMA運算95是定義為包含ExpDelta小于{-2}且EffSub為真的運算。值得注意的是，這些分類的定義僅為例示，FMA運算當可采不同方式進行分類。舉例來說，在另一實施例中，第二類與第四類可以用同一類表示，相同地，第三類與第五類也可以同一類表示。此外，在其他實施例中，圖2的數字線70的左部分與右部分的分隔線亦可改變。

融合FMA指令執行元件組

圖3是顯示一般用以執行FMA運算的融合FMA指令執行元件組100的一實施例。此元件組100包含兩個物理上與/或邏輯上分開的算術邏輯單元，(在一實施例中，即為一調整后的乘法器45與一調整后的加法器50)與共享儲存空間155與55以儲存多個未經舍入運算的中間結果向量與舍入指標(rounding indicator)。

各個調整后的乘法器45與調整后的加法器50都是一個指令執行單元，進一步來說，是指令管線24內的一個算術處理單元，用以對機器指令(例如復雜指令集(CISC)微架構內一個指定的指令集或是精簡指令集(RISC)微架構內一個指定的指令集)進行解碼，以及從一組共享的高速存儲器讀取運算元并寫入結果。指令執行單元可被理解為一個邏輯電路的特性集合，用以執行傳送過來的指定機器指令集，而不同于可平行執行(而不僅止于管線化執行)多個機器指令的較大的電路群(如果存在的話)。

更特別的是，調整后的乘法器45與調整后的加法器50互相分離、不可分割的、能獨立運行的執行單元，能獨立對微碼進行解碼并執行，并提供控制信號至內部的數據路徑。共享高速存儲器可以是一個暫存器檔案或是一組非架構運算暫存器，供微指令交換數據并使其運算結果可為其他執行單元看見。

更特別的是，調整后的乘法器45是一個適當的乘法運算單元，在大部分情況下，就像傳統的乘法運算單元，能執行不屬于FMA運算的一般乘法微指令。不過，此調整后的乘法器經適當調整，使能接收FMA乘數105、被乘數110、與累加數115作為其輸入運算元，并產生一儲存格式中間結果150，這在后續段落會有更進一步的描述。相類似地，調整后的加法器50是一個適當的加法運算單元，在大部分情況下，就像傳統的加法運算單元，能執行不屬于FMA運算的一般累加微指令，例如加或減。不過，此調整后的加法器經適當調整，使能接收儲存格式中間結果150并產生一個正確且經舍入運算的FMA結果。

調整后的乘法器45能夠執行第一階層或部分的融合FMA運算(FMA1子運算)。此調整后的乘法器45包含一輸入運算元分析器140、一乘法加總陣列120、一最終加法器125、一標準化移位器、與一前導位預測與編碼器135。在執行FMA1子運算時，調整后的乘法器45會產生并輸出一未經舍入運算的標準化加總結果145與多個舍入位(或是舍入指標)。相較之下，在執行非融合FMA運算時，調整后的乘法器45會產生一經舍入運算且相容于IEEE標準的結果。

舍入位與未經舍入運算的標準化加總結果145的最重要位依據一儲存格式進行儲存。在一實施例中，未經舍入運算的標準化加總結果145的最重要位輸出至一結果總線146，以儲存至一尾數寬度等于目標數據格式的尾數寬度的重命名暫存器155。舍入位輸出至一專用舍入位或運算控制指標數據路徑、或是位于調整后的乘法器外且不同于結果總線146的連接網路148，以儲存至一不同于儲存重命名暫存器155的儲存單元(例如重排緩沖器30)的舍入快取55。這些未經舍入運算的標準化加總結果145的最重要位，連同舍入位，包含一儲存格式中間結果150。

因為重命名暫存器155與舍入快取55屬于可為其他執行單元看見的共享存儲器的一部分，物理上與/或邏輯上獨立于調整后的乘法器45的調整后的加法器50，可以通過運算元總線152與舍入位數據路徑148接收此儲存格式中間結果150，并執行一第二(完成)階層或部分的融合FMA運算(FMA2子運算)。此外，在FMA1子運算與FMA2子運算間亦可執行其他不相關的運算。

調整后的加法器50提供一運算元乘數160，使FMA狀態下的累加運算元歸零，而在FMA狀態下，調整后的乘法器45已完成必要的累加運算。調整后的乘法器50并具有舍入位選擇邏輯175，從調整后的乘法器45產生的舍入位、調整后的加法器50內部產生的舍入位，或是二者的組合，選擇用于舍入模組180以產生最終舍入結果的舍入位。調整后的加法器并具有一近路徑加總電路165，用以在存在兩個加總運算元的塊消去的情況下對總數進行標準化運算，并具有一遠路徑加總電路170，用以執行最多只需單一位移位的加總運算以產生總數。如下所述，FMA2子運算可完全由遠路徑加總電路170進行處理。

調整后的乘法器

圖4和5是詳細顯示調整后的乘法器45的一實施例。圖4特別顯示調整后的乘法器45的路徑確認邏輯185與尾數乘法模組190。圖5特別顯示調整后的乘法器45的指數結果產生器260與舍入指標產生器245。

如圖4所示，路徑確認邏輯185包含一輸入解碼器200、一輸入運算元分析器140、路徑控制邏輯215與一累加數對準與射入邏輯電路220。尾數乘法模組190包含圖3的乘法加總陣列120，這在圖4中以二個元件顯示，即一乘法陣列235與一部分乘積加法器240。尾數乘法模組190并包含一最終加法器125、一前導位預測器與編碼器135、與標準化移位器130。

如圖5所示，指數結果產生器260包含一PNExp產生器265、一IRExp產生器270、與一不足位/溢位偵測器275。舍入指標產生器245包含一中間符號產生器280、一結果向量端口285、一端回進位指標290、一粘位產生器295與一舍入位產生器300。

請參照圖4，調整后的乘法器45通過一個或多個輸入端口195接收一輸入微指令以及運算元數值。就FMA微指令而言，調整后的乘法器45接收一被乘數運算元A、一乘數運算元B與一累加數運算元C，各個運算元都包含一符號指標或位、一尾數與一指數。在圖4與圖6中，浮點運算元的符號、尾數與指數部分分別以下標S、M與E表示。舉例來說，A_S、A_M、A_E分別代表被乘數的符號位、被乘數的尾數與被乘數的指數。

解碼器200對輸入微指令進行解碼以產生FMA指標M與二進位數運算符號指標(或位)P_S與O_S，M意指接獲FMA微指令。在一實施例中，形式為A*B+C的FMA微指令會產生二進位數零的一正乘法/向量負乘法符號運算子P_S與一加/減運算子O_S。形式為-A*B+C的負乘積-累加微指令會產生一個二進位數一的運算子P_S與一個二進位數零的運算子O_S。形式為A*B-C的乘積-相減微指令會產生一個二進位數零的運算子P_S與一個二進位數一的運算子O_S。形式為-A*B-C的向量負乘積-相減微指令會產生二進位數一的運算子P_S與運算子O_S。在其他較為簡化的實施例中，調整后的乘法器45并不直接支援向量負微指令與/或減法微指令，但由微處理器10來支援等效的運算，也就是在調用乘積-累加/相減微指令至調整后的乘法器45前，視情況額外反轉一個或多個運算元或符號指標。

乘法陣列235接收被乘數與乘數的尾數值A_M與B_M并計算出A_M與B_M的部分乘積。可以理解的是，當A_M或者B_M的絕對值為一或零，乘法陣列235所產生的單一個“部分乘積”的值就會是A_M與B_M的完整乘積。部分乘積提供至部分乘積加法器240，其提供多個項目以接收A與B的部分乘積以等待將其加總，而至少一個的部分乘積加法器240的項目用以接收一累加來源值C_X。如下所述，在討論完輸入運算元分析器140與累加數對準射入邏輯220后，會對部分乘積加法器240有其他的說明。

輸入運算元分析器140包含一ExpDelta分析子電路210與一EffSub分析子電路205。ExpDelta分析子電路210產生ExpDelta(ExpΔ)值。在一實施例中，ExpDelta通過將乘數與被乘數的輸入指數值A_E與B_E加總，減去加數或減數輸入指數值C_E，并在存在指數偏移值ExpBias時減去此指數偏移值(如果任一者存在)。在A_E、B_E與C_E是以偏移指數(biased exponent)表示時，例如IEEE754的規范，被乘數A與乘數B的乘積的偏移量將會是累加數C偏移量的兩倍。而導入ExpBias值可對此進行校正。

EffSub分析子電路205分析運算元符號指標A_S、B_S與C_S以及運算元符號指標P_S與O_S。EffSub分析子電路205產生一“EffSub”值，用以表示FMA運算是否為一有效減法運算。舉例來說，若是對A與B的乘積與C執行運算元特定的加法或減法運算(或是在負向量乘法運算子的情況下，此運算結果的負值)所產生的結果R的絕對值小于(a)A與B的乘積的絕對值或是(b)C的絕對值，就會是有效減法。若以數學符號表示，若是(|R|<|A*B|)∨(|R|<|C|)，其中R為FMA運算的結果，此FMA運算就會構成有效減法。雖然以FMA運算的結果可以簡化EffSub的描述，不過需理解的是，在EffSub分析子電路205預先確認EffSub時，實際上是通過分析符號指標A_S、B_S、C_S、P_S與O_S來進行，而不去評估A、B與C的尾數、指數與大小。

路徑控制邏輯215接收由輸入運算元分析器140產生的ExpDelta與EffSub指標，并借以產生一路徑控制信號，其數值以變數Z表示。路徑控制邏輯215可控制C的累加運算是否會連同A與B的部分乘積一并在調整后的乘法器45內執行。在一實施例中，路徑控制邏輯215用以產生Z的設定條件顯示于圖2中。在一實施例中，對于任何調整后的乘法器45被選用來執行乘積-累加運算的累加部分運算的情況合(例如類型1，2與4)，Z會是二進位數一，而對于任何ExpDela與EffSub的其他組合(例如類型3與5)，Z會是二進位數零。

另外，路徑控制邏輯215也可以通過判斷C所具有一大小，相較于A與B的乘積大小，是否可使C對準于加總樹(summation tree)內，而不需將C的最重要位移位至A與B的部分乘積加總的加總樹所提供的最重要位的左側來產生Z。另一個或替代的設定條件可以是，在執行FMA運算時是否具有執行塊消去的潛力。再另一個或替代的設定條件可以是，對A與B的乘積進行C的累加運算所產生的舍入前結果R所需要的位數，是否少于將C對準A與B的乘積所需要的位數。由此可知，路徑控制的條件可響應調整后的乘法器45的設計進行改變。

累加數對準射入邏輯220接收路徑控制邏輯215所產生的Z、ExpDelta分析子電路210所產生的ExpDelta、一移位常數SC、與累加數尾數值C_M。在一實施例中，此累加數對準射入邏輯220亦接收C_M的位反相(bitwise negation)，即，與加法/減法累加運算子指標O_S。在另一實施例中，累加數對準射入邏輯220在加法/減法累加數指標O_S顯示調整后的乘法器45所接收的微指令為乘積-相減微指令時，選擇性地額外反轉C_M的值。

相應于所接收的輸入，累加數對準射入邏輯220會產生一數值C_X射入部分乘積加法器240。此射入陣列的C_X的寬度是2m+1，或可理解為輸入運算元的尾數A_M、B_M與C_M的兩倍寬度額外加上一個位。

若是M為二進位數零以顯示調整后的乘法器45正在執行一般的乘法運算而非FMA1子運算，多工器230就會將一舍入常數RC，而非C_X，射入部分乘積加法器240，借此，調整后的乘法器45即可以傳統方式產生一舍入后結果。RC的數值部分是由指令顯示的舍入運算的類型所決定(例如：舍入向上(round half up)、舍入相等(round half to even)、舍入遠離零(round half away from zero))，部分是由輸入運算元的位尺寸(例如32位與64位)所決定。在一實施例中，部分乘積加法器240利用兩個不同的舍入運算常數來計算出兩個總數，并選擇其中較適當的一個。借此，調整后的乘法器45的IMant輸出就會是一般乘法運算的正確舍入后的尾數結果。

若是M為二進位數一而Z為二進位數零，即表示不需對A與B的乘積執行C的累加運算，在此情況下，就一實施例而言，此累加數對準射入邏輯220會將C_X設定為零，而使多工器230將零值射入用以接收C_X值的部分乘積加法器240陣列。若是M為二進位數一且Z為二進位數一，累加數對準射入邏輯220就會將C_X右移相等于ExpDelta加上一移位常數SC的量，以產生C_X。在一實施例中，移位常數SC等于2，以對應于圖2，當C的累加運算執行于調整后的乘法器內，圖中數字空間內最大的ExpDelta負值。隨后，多工器230會將運算結果C_X射入部分乘積加法器240。

累加數對準射入邏輯220內并結合有一粘收集器(sticky collector)。累加數C_X中任何移位超過部分乘積加法器240加總樹的最不重要位的部分，保留于XtraStky位供舍入運算之用。因為會有多達m個位移位超過部分乘積加法器240加總樹的最不重要位，XtraStky位作為一寬度m的額外粘位陣列，用于粘位S的運算。

回到調整后的乘法器45的加法邏輯，在部分實施方式中，部分乘積加法器240為一加總樹，而在一實施方式中，為一個或多個進位儲存加法器。此部分乘積加法器240根據所提供的部分乘積加總樹的位欄的進位儲存向量，對一未經舍入的冗余代表或總數，依據現有技術的乘法執行單元通常會執行的運算方法，來進行累加運算，這包含在部分乘積的累加運算中，對累加數輸入值選擇性進行額外的位反相與對準運算。

同樣地，部分乘積加法器240所執行的算術運算會受到Z的數值的影響。若是Z＝1，部分乘積加法器240就會對于A_M與B_M的乘積執行C_X的連帶累加運算(joint accumulation)。若是Z＝0，部分乘積加法器240就會對A_M與B_M的乘積執行一基本累加運算。部分乘積加法器240會產生一由一2m位總數向量與一2m位進位向量表示的冗余二進位數總數，作為連帶累加運算或是基本累加運算的運算結果。

這些進位與總數向量同時轉送至一最終加法器125與一前導位預測器與編碼器135。此最終加法器125可為一進位預看加法器(carry-lookahead adder)或一進位傳播加法器(carry propagate adder)，通過將進位與總數向量轉換成寬度為2m+1的正或負的預標準化未舍入非冗余總數(prenormalized unrounded nonredundant sum)PNMant以完成累加運算程序。最終加法器125并產生一總數符號位SumSign，來顯示PNMant為正數或負數。

在最終加法器125產生PNMant的同個時間周期，前導位預測器與編碼器135會同步預測需要被消除以標準化PNMant的前導位的數量。相較于傳統對乘積-累加運算分工處理的FMA設計中，因其最終加法器125執行的最終加法運算是于標準化運算后執行而需同時對進位向量與總數向量執行標準化運算，因而必須等待前導位預測的輸出，故本發明的處理方式相較傳統作法實具有優點。在一實施例中，此前導位預測器與編碼器135不是可以適用于正總數的情況，就是可適用于負總數的情況。

在一實施例中，前導位預測只在類型1的運算執行。如前所述，所選擇的前導位預測的方法不是可以適用于正總數就是可以適用于負總數，為熟習浮點運算設計領域者所熟知。

因為前導位預測器與編碼器135具有最多一個位的誤差，任何可用于校正此誤差的常用技術均可使用，這些技術可設置于標準化移位器130內，或是關聯于標準化移位器130。一個解決方案提供邏輯來預測此誤差。另一個解決方案通過確認PNMant的MSB是否已經設定，并相應地選擇PNMant的一額外移位。

標準化移位器130從最終加法器125接收此未舍入非冗余總數PNMant并產生一原始尾數值GMant。在C_X的累加運算是由部分乘積加法器240執行的情況下，GMant會是A_M和B_M乘積與C_X的標準化加總的絕對值。而在其他情況下，GMant會是A_M和B_M乘積的標準化加總的絕對值。

為了產生GMant，標準化移位器130在SumSgn顯示PNMant為負時對PNMant執行位反相的運算。對負的PNMant數值執行標準化移位器130的位反相運算，可產生如下所述的儲存格式中間結果150，并有助于正確的舍入運算。在調整后的乘法器內反轉PNWant，即可產生一正數提供給調整后的加法器，而不需先知會PNWant的數值為負。此處理方式可使累加運算實施起來就像加總運算并以簡化的方式進行舍入運算。

此外，此標準化移位器130會將PNMant左移一個由LDP、EffSub與Z的函數所計算出來的量。值得注意的是，即使沒有發生最重要前導位的消除，仍需要將PNMant左移零、一或二個位位置以產生一有用的標準化儲存格式中間結果150，以確保后續的舍入運算可正確進行。此標準化運算由一個左移所構成，以將算術上最重要位移動至標準化的最左位置，使能表示于如下所述的儲存格式中間結果150。

相較于傳統的FMA設計，此實施方式具有三個額外的優點。第一，此實施方式不需在部分乘積加法器240內插入額外的進位位(若響應于EffSub對累加數尾數執行2’補數時有此需求的話)。第二，此實施方式不需提供一大的符號位偵測器/預測器模組，來檢測并選擇性補足非冗余部分乘積與累加數加總值的冗余總數與進位向量表示。第三，此實施方式不需輸入額外的進位位來確保部分乘積與累加數加總運算中，選擇性補足的總數與進位向量表示的運算正確。

關于圖5的指數結果產生器260，PNExp產生器265產生一預標準化指數值PNExp，此數值為被乘數與乘數指數值A_E與B_E、指數偏移值ExpBias與移位常數SC的函數。在一實施例中，PNExp以算式SC+A_E+B_E-ExpBias來計算。

IRExp產生器270使PNExp遞減，作為標準化移位器130執行的尾數標準化運算，以產生一中間結果指數IRExp。此數值為PNExp與前導位預測(leading digit prediction,LDP)的函數。隨后，IRExp轉送至如下所述的結果向量端口280。

中間符號產生器280產生中間結果符號指標IRSgn，其為EffSub、E、A_S、B_S與Z的函數。在一實施例中，IRSgn在某些情況下以被乘數符號位A_S與乘數符號位B_S的邏輯互斥或來計算。不過，若是Z位為二進位數一顯示累加運算已經執行，EffSub也是二進位數一顯示有效減法，而E位值為二進位數零顯示沒有等待中的端回進位(end-around carry)，IRSgn就會以被乘數符號位A_S與乘數符號位B_S的邏輯互斥或的反相值(XNOR)來計算。換句話說，中間符號通常是A與B的乘積的符號。當累加數的大小大于A與B的乘積時，A與B的乘積的符號會反轉，乘積-累加運算會是一有效減法運算，而累加運算的完成不需要使用端回進位(因為累加運算為負)。

中間結果符號指標IRSgn用于一可用以確認最終符號位以供具塊消去可能的FMA運算使用的創新方法。不同于傳統的分路FMA實施方式，此實施方式不需要符號預測器，也不需要用以預測符號的大量電路。另外，零結果的符號，或是具有符號零輸入的運算結果的符號，容易預先計算，來納入例如一舍入模式輸入。

結果向量端口280輸出一儲存格式中間結果向量IRVector，其包含中間結果指數IRExp、中間結果符號IRSgn與中間結果尾數IRMant。在此儲存格式的一實施例中，IRMant包含GMant的最重要m位，其中m為目標數據類型的寬度。舉例來說，在IEEE雙精確度(double precision)運算中，結果向量端口280輸出IRVector作為單一個符號位、十一個指數位、與GMant最重要53位的組合。在儲存格式的另一個實施例中，m等于A_M、B_M與C_M的尾數的寬度。在儲存格式的又一個實施例中，m大于A_M、B_M與C_M的尾數的寬度。

類似于IEEE的標準儲存格式，這些尾數位中的單一個最重要位作為儲存時的一隱含值。IRVector儲存至一共享存儲器，例如重排緩沖器30的重命名暫存器155，借此，其他指令執行單元就可存取IRVector，且/或IRvector可通過一結果轉送總線(forwarding bus)40轉送至其他指令執行單元。在一實施例中，IRVector儲存至一重命名暫存器155。此外，不同于架構暫存器會對重排緩沖器給予一固定不變的任務分派，中間結果是向量在重排緩沖器內給予一不可預期的任務分派。在另一實施例中，IRVector暫時儲存于將用以儲存FMA運算的最終舍入結果的目標暫存器內。

現在請參照圖5的舍入指標產生器245，不足位/溢位偵測器275產生不足位指標U₁與溢位指標O₁，其為IRExp與指數范圍值ExpMin與ExpMax的函數。指數范圍值是與儲存格式中間結果150(下面將有進一步討論)的精確度或目標數據類型有關。若是IRExp小于可代表此FMA運算目標數據類型的指數值的范圍，或是小于可代表的任何中間儲存空間，例如重命名暫存器，的指數值的范圍，U₁位就會是二進位數一，否則U₁位就會是二進位數零。相反地，若是IRExp大于可代表此FMA運算目標數據類型的指數值的范圍，或是大于可代表的任何中間儲存空間，例如重命名暫存器，的指數值的范圍，O₁位就會是二進位數一，否則O₁位就會是二進位數零。另外，U與O可經編碼以表示四個可能的指數范圍，其中至少一個編碼會表示不足位，而至少一個編碼會表示溢位。

在傳統一般乘法單元的實施方式中，U₁與O₁位會報告至例外事件控制邏輯。不過，在執行FMA1子運算時，調整后的乘法器45會輸出U₁與O₁位至中間儲存空間以供調整后的加法器50執行。

端回進位指標產生器290會產生等待中的端回進位指標E₁位，其為Z、EffSub與SumSgn的函數。若是已確認的Z位的數值為二進位數一，表示部分乘積加法器240已經執行C的累加運算，已確認的EffSub變數顯示此累加運算造成一有效減法，并且SumSgn顯示所產生的未舍入非冗余值PNMant為正，E₁位就會是二進位數一。在其他情況下，E₁就會是二進位數零。

結果向量端口280儲存GMant的最重要位作為中間結果向量的中間結果尾數，而粘位產生器295與舍入位產生器300會使剩下較不重要的位(例如超出中間結果尾數的第53個位的位)減少至剩下舍入(R₁)與粘(S₁)位。粘位產生器295產生粘位S₁，其為SumSgn、Z、GMant的最不重要位、EffSub與XtraStky位的函數。舍入位產生器300產生舍入位R₁，其為GMant的最不重要位的函數。

舍入快取

舍入位端口305會輸出各個位U₁、O₁、E₁、S₁、R₁與Z，借此，這些位就可以被其他執行單元(例如調整后的加法器50)使用來產生FMA運算最終的舍入后結果。為了方便說明，這些位在本文中都表示為舍入位，即使其中有部分位會在產生FMA運算最終結果的過程中有其他用途，又即使并非所有的位都用于舍入運算。舉例來說，在某些實施方式中，O₁位就不會用于舍入運算。這些位可互換地被指為運算控制指標。舉例來說，位Z與E，即指出那些后續運算需要執行；位U與O，即指出這些運算應如何執行。此外，這些位可表示為運算間歇狀態值(calculation intermission state value)，因為他們提供一壓縮格式(compact format)來表示與選擇性地儲存在調整后的乘法器45的FMA1子運算與調整后的加法器50的FMA2子運算間的間歇時間中的運算狀態信息。

這些位，無論被稱為舍入位、運算控制指標、運算狀態指標或其他，連同中間結果向量與累加數值C，除了運算元數值，還提供后續指令執行單元需要的任何事物，以產生算術上正確的最終結果。換句話說，中間結果向量與舍入位的結合可提供算術上正確表示FMA運算結果所需的任何結果，此運算結果與一具有±A*B±C形式但變為目標數據尺寸的無限精確FMA運算的運算結果無從辨別。

依據本發明的一實施例，微處理器10用以將舍入位儲存至舍入快取55內，并將舍入位通過轉送總線40轉送至其他指令執行單元，此舍入快取55亦可稱為運算控制指標儲存空間。依據本發明的另一實施例，微處理器10并不具有舍入快取55，而僅將舍入位通過轉送總線40轉送至其他指令執行單元。依據本發明的又一實施例，微處理器10將舍入位儲存至舍入快取55內，但不提供轉送總線40來將舍入位直接轉送至其他的指令執行單元。

指令快取55與所儲存的指令位或運算控制指標為非架構，亦即其非為終端用戶所能看見。相較之下，架構暫存器或架構指標(例如浮點狀態字(floating point status word))則是可以被程序人員看見且指定為架構指令集的一部分的信號來源。

在此所描述的舍入位僅為例示，而不同的實施方式會產生不同的舍入位組。舉例來說，在另一實施例中，調整后的乘法器45亦包含一保護位產生器以產生一保護位G1。在另一實施例中，調整后的乘法器亦對一零結果(zero result)的符號執行一預運算，并將其值儲存于舍入快取。若是調整后的加法器50后續運算的結果為零結果，舍入加法器50就會使用此儲存的零結果符號指標來產生最終的帶符號零結果。

依據本發明的另一實施例，舍入快取55是一位于調整后的乘法器45外部的存儲器儲存空間。不過，在另一個不同的實施例中，此舍入快取55結合于調整后的乘法器55內。

尤其是在一實施例中，此舍入快取55未經結果總線而獨自連接至指令執行單元。有鑒于結果總線用以將結果從指令執行單元傳送至一通用儲存空間，舍入快取55獨自連接至結果總線55而未經結果總線。此外，運算控制指標儲存空間僅能為用于儲存或載入運算控制指標的指令所存取。借此，即可通過輸出指令結果的結果總線以外的其他機制來存取舍入快取55，舉例來說，可通過舍入快取自身的導線。此外，亦可通過指令執行單元的輸入運算元端口外的其他機制來存取舍入快取55。

在一實施例中，舍入快取55是一完全關聯(fully associative)的可存取存儲器，其具有的寫入端口的數量相當于可平行分派的FMA1微指令的最大數量；其具有的讀取端口的數量相當于可平行分派的FMA2微指令的最大數量；而其深度(項目數量)關聯于指令排程的容量，與FMA1微指令分派后而在指令排程分派FMA2微指令前所能清空的最長時間周期(以時鐘周期計)。另一實施例使用較小的舍入快取55，而微處理器10在舍入快去55內無法取得儲存FMA1微指令的舍入位結果的空間時，重新執行FMA1微指令。

快取的各個項目儲存快取數據與相關聯的旗標值(tag value)，此旗標值可與用以辨識儲存有儲存格式中間結果向量的重命名暫存器155的旗標值相同。在微處理器10準備(prepare)/拿取(fetch)供第二使用的運算元時，微處理器10使用重排緩沖器索引(ROB index)來由重命名暫存器155取回所儲存的中間數據，與此相同的索引將會提供至舍入快取55，并提供中間結果150的剩下部分(即運算控制指標)。

其優點在于，本發明的配置給舍入快取55的物理上儲存項目的數量明顯少于配置給重命名暫存器155的項目數量。重命名暫存器155的數量是進行中(in flight)的微指令數量與需要使非循序微處理器或設計的執行單元飽和所需的暫存器名稱數量的函數。比較起來，舍入快取55所需的項目數量則為進行中的FMA微指令的可能數量的函數。因此，在一未受限的實例中，微處理器的核可提供六十五個重命名暫存器155，但只提供八個舍入快取55的項目提供給至多八個平行處理的算術運算。

本發明的另一實施例擴充用以儲存中間結果向量的重命名暫存器155(即擴大重命名暫存器的寬度)，以提供額外的位供舍入快取55使用。此實施例雖非本發明空間利用的最佳者，但亦屬于本發明的范圍內。

舍入位連同中間結果指標IRVector包含儲存格式中間結果150。此儲存格式依據一標準數據格式儲存與/或傳送未舍入標準化加總結果145的最重要位(即具有默認值的位)，并且將未舍入標準化加總結果145的剩下位(縮減或未縮減)，連同E₁、Z、U₁與O₁位，進行儲存與/或傳送，因而相較于現有技術具有顯著的優勢。

調整后的加法器

現在請參照圖6，調整后的加法器50包含一運算元調整器60、對準與條件邏輯330、以及一個與一單一位溢位移位邏輯345配對的遠路徑累加模組340。此運算元調整器160并包含一指數產生器335、一符號產生器365、一加法器舍入位產生器350、舍入位選擇邏輯175與一舍入運算模組180。

值得注意的是，在本發明的一實施例中，調整后的加法器50具有一分路設計而使其通過各自獨立的近運算與遠運算來計算結果，此技術為浮點運算設計的技術人員所已知。近路徑的計算能力需要一個與一多位標準化移位器(未圖示)配對的近路徑加總模組(未圖示)，此等能力未在圖6中顯現。在一實施例中，運算元C與D的輸入指數值的差值位于{-1,0,+1}內而構成有效減法的一般加總運算會被導向至近路徑16，其他的加法運算則會被導向至遠路徑170。其優點在于，本發明可使調整后的加法器50的所有的FMA2子運算都被導向至遠路徑170。

調整后的加法器50提供一個或多個輸入端口310以接收一個微指令與兩個輸入運算元。第一輸入運算元D是一被減數或一第一加數。第二輸入運算元C是一減數或一第二加數。在浮點運算的實施例中，各個輸入運算元包含一輸入符號、一指數、與一尾數值，分別以下標S、E與M表示。通過解譯微指令，解碼器315利用信號QS指出此運算究竟為一加法或是一減法運算。通過解譯微指令(或是由微指令指令的一運算元參考)，解碼器并可以利用信號M來指出此微指令是否支配一個特定的微操作可使調整后的加法器50執行FMA2子運算。

在調整后的加法器50被賦予執行FMA2子元運算的任務時，調整后的加法器50接收由調整后的乘法器45先前執行相對應的FMA1子運算所產生的中間結果向量IRVector。因為中間結果向量IRVector的寬度僅為m個位，調整后的加法器50不需(而在一實施例中，不會)被調整成可接收或執行多于m個位的有效位數。因此，相較于以較寬位數呈現的IRVector，本實施例可以簡化內部數據路徑、累加模組340與調整后的加法器50的其他電路，并使其運作更有效率。此外，因為涉及塊消去的累加運算由調整后的乘法器45完成，在調整后的加法器50的近/塊消去路徑上不需加入舍入運算邏輯來正確計算出FMA結果。

在一實施例中，調整后的加法器50從重命名暫存器155接收IRVector。在另一實施例中，則是從轉送總線40接收IRVector。而在圖6所示的實施例中，IRVector被接收為運算元D。此調整后的加法器50接收累加數值C作為另一個運算元。

若是M顯示調整后的加法器50被賦予執行FMA2子元運算的任務，運算元調整器160就會在Z是二進位數一時，將輸入運算元的一部分設定為等同于二進位數零，以顯示C的累加運算已經由調整后的乘法器45執行。在一實施例中，各個指數、尾數與符號的欄位C_E、C_M與C_S均調整為零。在另一實施例中，只由指數與尾數的欄位C_E、C_M調整為零，至于符號的欄位C_S則維持原樣。借此，調整后的加法器50即可將加數D加上一帶符號的二進位數零。

一個二進位數一的M位并通知調整后的加法器50接收由調整后的乘法器45所產生的舍入位，并將其并入儲存格式中間結果150。

在其他所有情況中，即Z為二進位數零或是M為二進位數零以顯示調整后的加法器50被賦予傳統累加運算的任務，運算元調整器160只會對指數與尾數欄位C_E與C_M進行傳統浮點加法運算需要的調整。

在一實施例中，運算元調整器160包含一對多工器接收Z的值，而在C_M與零之間以及C_E與零之間進行選擇。選定的值在圖6中以C_M*與C_E*表示。隨后，對準與條件邏輯330將對準與/或調節此選定值C_M*與第一運算尾數DM。

接下來，遠路徑累加模組340將C_M*與DM相加。在一實施例中，此累加模組340為一雙加加法器，以提供總數與漸增總數。在一實施例中，此累加模組340利用1’補數(one’s complement)來執行有效減法。若是此總數會在尾數欄位產生一位的溢位，溢位移位邏輯345就會條件地將總數移動一個位，以使結果值完成舍入運算的準備。

指數產生器335利用選定的指數值C_E*、第一運算元指數DE、與由溢位移位邏輯345產生的移位量來產生一最終指數FExp。

符號產生器365依據由第一與第二運算元C_S與D_S、加/減運算子QS與加總結果符號構成的函數來產生一最終符號FSgn。

在另一實施例中，運算元調整器160以選擇器邏輯取代。當輸入解碼器顯示加法器正在執行FMA2子運算而Z是二進位數一以顯示C的累加運算已執行，此選擇器邏輯會使第一運算元D直接轉送至舍入運算模組180，但使加總邏輯維持在休眠狀態(quiescent state)。

調整后的加法器50的邏輯產生一組自己的舍入位R₂、S₂、U₂、O₂與E₂。當M顯示調整后的加法器50被賦予執行FMA2子運算的任務時，調整后的加法器50也會接收多個由執行FMA1子運算的調整后的乘法器45事先產生的舍入位R₁、S₁、U₁、O₁、Z與E₁。

在M為二進位數一的情況下，舍入位選擇邏輯175會確認來自調整后的乘法器45的舍入位E₁、R₁與S₁、來自調整后的加法器50的舍入位E₂、R₂與S₂、或是二者的某些混合或組合，將會被加法器的舍入運算模組180用以產生最終的舍入后尾數結果。舉例來說，若是所執行的運算并非FMA2子運算(即M＝0)，舍入運算模組180就會使用加法器產生的舍入位E₂、R₂與S₂。另外，若是累加運算由調整后的乘法器45執行(即M＝1且Z＝1)，并且不存在不足位的情形(即UM＝0)，就由乘法器產生的舍入位E₁、R₁與S₁來提供舍入運算模組180產生最終舍入后結果所需的任何物件。

此可變位置的舍入運算模組作為調整后的加法器50的遠計算功能的部分來設置。而在一實施例中，此舍入運算模組配合由1’補數有效減法所造成的正差值舍入運算，并且還配合由非有效減法的加總運算所造成的正總數舍入運算。此舍入運算模組180以類似于傳統單一加/減單元執行的方式，執行選定的舍入位RX、黏位SX，而在有提供的時候也會執行保護位G_X(未圖示)。此舍入運算模組180由傳統設計進行修改以接收至少一補充輸入，即選定的端回進位位EX，而若是由調整后的乘法器45執行1’補數有效減法，即可顯示需要一端回進位校正。使用選定的RX、SX與EX輸入，舍入運算模組180可正確地對中間結果向量與帶符號零的加總執行舍入運算，以產生正確而符合IEEE標準的結果。此為浮點運算設計的技術領域人員所能理解。

如前述，調整后的加法器50需要近路徑165來執行某些類型的傳統累加運算，但不需要近路徑165來執行本文所述的FMA運算。因此，在執行本文所描述的FMA運算類型時，近路徑邏輯165會在FMA運算的過程中維持休眠狀態以降低耗能。

第一與第二FMA子運算

圖7至10顯示本發明利用一第一FMA子運算(FMA1)與一第二FMA子運算(FMA2)執行一不可分割分路乘積-累加運算的方法的一實施例。其中，FMA2子運算并非臨時性相接于FMA1子運算，也不是物理性上相接于FMA2子運算。

圖7顯示FMA1子運算的一路徑確認部分。在步驟408中，FMA1子運算確認EffSub變數。當EffSub為二進位數一，即顯示是否累加數運算元與乘數運算元的乘積的累加運算會構成一有效減法。在步驟411中，FMA1子運算選擇性地對累加數運算元執行位反相的運算。在步驟414中，FMA1子運算計算ExpDelta。ExpDelta等于乘數與被乘數的指數的加總減去累加數的指數與一指數偏移。ExpDelta不只確認乘數尾數與累加數尾數的相對對準以供加法運算之用，也會配合EffSub變數來確認累加數運算元的累加運算是否將由FMA1子運算執行。

在步驟417中，FMA1子運算確認路徑控制信號Z。當數值為二進位數一，即表示有一個累加數運算元的加總運算，會利用調整后的乘法器45電路，在FMA1子運算中執行。在一實施例中，FMA1子運算在ExpDelta大于或等于負一時，將二進位數一指派給Z，而在ExpSub為一且ExpDelta為負二時，也會將二進位數一指派給Z。其他的實施方式會以不同方式分割ExpDelat與EffSub的數字空間。

圖8是FMA1子運算的乘法與條件累加部分的方塊示意圖。在步驟420中，FMA1子運算選擇一累加路徑供累加運算元使用。若是Z為二進位數零，如步驟426所示，FMA1子運算就會計算乘數運算元的部分乘積的加總，而不加上累加數運算元。另外，若是Z為二進位數一，如步驟423所示，FMA1子運算會調整選擇性互補累加數尾數的對準值，其調整量為ExpDelta值的函數。就一實施例而言，此調整量等于ExpDelta加上一移位常數。

在步驟426/429中，FMA1子運算執行一第一累加運算，其為(a)乘數和被乘數運算元的部分乘積(即步驟426)，或是(b)累加數運算元與乘數和被乘數運算元的部分乘積(即步驟429)。在步驟432中，FMA1子運算條件執行一前導位預測，來預測總數的最重要前導位所需要的消去。前導位預測的運算限于類型1的FMA運算75，并且會與步驟429中部分的加總運算平行執行。另外，前導位預測邏輯可連接至步驟426或步驟429以處理其運算結果。

經過步驟426或429，以及步驟432的執行后，FMA1子運算會產生一未經舍入、非冗余的標準化加總結果145(如步驟435所示)。接下來，FMA1子運算會產生一儲存格式中間結果150(如步驟438所示)。一旦儲存格式中間結果150被儲存或分派至轉送總線40，FMA1子運算就會終止，并釋放執行FMA1子運算的資源(例如作為調整后的乘法器45的指令執行單元)給其他與FMA運算無關的運算使用。所屬技術領域人員當可理解，此技術亦可同樣適用于可同時通過連續階段執行多個運算的管線乘法器。

圖9A與9B詳細說明產生儲存格式中間結果150的程序。在步驟441中，FMA1子運算確認是否因累加數的累加運算構成有效減法，而存在待定的端回進位校正。若是Z與EffSub均為二進位數一(即類型1的FMA運算75或是類型4的FMA運算90)，并且由步驟435所產生的未經舍入非冗余的結果為正，FMA1子運算就會將二進位數一指派給變數E₁。

在步驟444中，FMA1子運算通過對尾數執行位反相的運算，而產生一原始尾數結果(germinal mantissa result,GMant)。若運算結果為負，就通過移位，將尾數標準化為一標準儲存格式。

在步驟447中，FMA1子運算產生一中間結果符號位(IRSgn)。若是E為二進位數零，而Z與EffSub均為二進位數一，IRSgn就會是被乘數與乘數的符號位的反邏輯互斥或結果。否則，IRSgn就會是被乘數與乘數的符號位的邏輯互斥或結果。

在步驟453中，FMA1子運算將SC加上乘數與被乘數的指數值加總，再減去ExpBias，以產生PNExp。

在步驟456中，FMA1子運算通過減少PNExp來處理PNMant的標準化運算，借以產生中間結果指數值(IRExp)。

在步驟459中，FMA1子運算確認中間不足位(U₁)與中間溢位(O₁)位。

在步驟462中，FMA1子運算由原始尾數(GMant)的最重要位產生一中間結果尾數(IRMant)。

在步驟465中，FMA1子運算將構成中間結果向量IRVector的IRSgn、IRMant與IRExp，儲存至儲存空間，例如一重命名暫存器。

在步驟468中，FMA1子運算會將GMant的LSB_S與部分乘積加法器240的移出位(Xtrastky)縮減至舍入位(R₁)與粘位(S₁)。而在另一實施例中，還包含一保護位(G1)。

在步驟471中，FMA1子運算將R₁、S₁、E₁、Z、U₁與O₁位紀錄于舍入快取55，而在提供有G1位時，也會一并記錄于舍入快取55。

圖10是一方塊圖顯示本發明不可分割分路FMA運算的一第二FMA子運算。

在步驟474中，FMA2子運算接收先前儲存在例如重命名暫存器的儲存空間內的中間結果向量IRVector。另外，FMA2子運算亦可由轉送總線接收IRVector。

在步驟477中，FMA2子運算接收先前儲存在例如舍入快取55的儲存空間內的舍入位。另外，FMA2子運算亦可由轉送總線接收舍入位。

在步驟480中，FMA2子運算接收累加數輸入值。

在決定步驟483中，FMA2子運算檢視步驟474所接收的Z位。若是Z位為二進位數一(或真)表示累加數的加總運算已經由FMA1子運算執行，此流程就會前進至步驟486。否則就會前進至步驟489。

在步驟486中，FMA2子運算將累加數輸入值的指數與尾數欄位調整為零。在一實施例中，FMA2子運算并不調整輸入累加數的符號位。隨后在步驟492中，此FMA2子運算會將計算中間結果指數與一帶符號零運算元的總數。接下來前進至步驟494。

在步驟489中，FMA2子運算計算中間結果指數與累加數的總數。接下來前進至步驟494。

在步驟494中，FMA2子運算利用FMA1子運算產生的Z、U₁、O₁位以及FMA2子運算產生的U₂與O₂位，從舍入位E₁、E₂、R₁、R₂、S₁與S₂中，選擇會用來對總數的尾數進行正確舍入運算的舍入位。

在步驟496中，FMA2子運算利用選定的舍入位來對總數進行正確的舍入運算。此FMA2子運算在執行尾數舍入程序的同時，選擇性地使IRExp遞增(步驟498)。如此，FMA2子運算即可產生一最終經舍入的結果。

圖7至10中所描述的部分步驟可不需圖示順序執行。此外，第七至十圖中所描述的部分步驟亦可平行執行。

運算類型的應用

此章節說明前述應用于圖2的五種不同運算“類型”的各種變數數值間的功能性關聯，尤其著重于PNMant的運算、符號與標準化處理以及與各個數據類型相關的EffSub、ExpDelta、Z、E與IntSgn的數值。

第一類型

如圖2所示，類型1的FMA運算75的特點在于，此運算涉及一有效減法(因此，EffSub＝1)，而調整后的乘法器45被選定以執行C的累加運算(因此，Z＝1)，而C的大小相當接近A和B的乘積(即-2<＝ExpDelta<＝1)而會造成塊消去的產生。

因為累加運算將會于調整后的乘法器45內執行而造成有效減法(即EffSub＝1且Z＝1)，累加數對準與射入模組220會在將累加數運算元尾數值C_M射入部分乘積加法器240前，對累加數運算元尾數值C_M造成與/或選擇一位反相運算。相對于部分乘積，此累加數對準與射入模組220會利用ExpDelta，來對準部分乘積加法器240內的累加數尾數。

隨后，對于未經舍入的非冗余數值145(即PNMant)的完整加總運算依照傳統乘法執行單元通常采用的方法來執行，此執行包含部分乘積的加總運算內，額外被選擇性位求與相對準的累加數輸入值。因而PNMant即可以1’補數的形式，表示乘數與被乘數尾數值以及累加數尾數值間的算數差。

PNMant可為正或負。若是PNMane為正就需要端回進位，而等待中的端回進位指標E₁就會被指派為二進位數一。若是PNMant為負就不需要端回進位，而E₁就會被指派為二進位數零。E₁被指派的值不僅為PNMant的函數，亦為Z與EffSub的值的函數，而在類型1的運算75中，Z與EffSub會是二進位數一。

在部分乘積與累加數輸入加總運算的同時，也會執行前導位預測來對任何最重要前導位需要的任何消去進行預測。如前述，于本發明一實施例中，此運算由一與最終加法器125并行的電路，于執行PNMant的加總運算時執行。

如浮點運算設計的技術領域人員所能理解，即使沒有發生前導位的相減消去，可能還是需要對PNMant執行一個零、一或二位位置的標準化運算，利用SC至PNExp來使其對準于所需的儲存格式，以供本發明描述與使用的中間結果150之用。若存在塊消去，顯然就會需要更多的移位運算。同樣地，若是PNMant為負，就會對此數值執行位反相的運算。對PNMant執行選擇性標準化與位反相運算用以產生原始尾數值GMant，其最重要m位變成中間結果尾數IRMant。

中間結果符號IRSgn不是被乘數符號位A_S與乘數符號位B_S的邏輯XOR運算結果，就是其邏輯NXOR運算結果，端視E₁的數值而定。若是E₁為二進位數一，IRSgn會被計算為被乘數符號位與乘數符號位的邏輯XOR運算結果。若是E₁為二進位數零，IRSgn就會被計算為被乘數符號位與乘數符號位的邏輯XOR運算結果。

回到FMA2運算，調整后的加法器50會接收包含路徑控制信號Z在內的已儲存或轉送的舍入位，因為Z為1，中間結果向量IRVector需要執行舍入運算，而會對最終的乘積-累加結果產生些微調整。在一實施例中，調整后的加法器50將中間結果向量IRVector與一零運算元(或是在另一實施例中，一帶符號二進位數零的運算元)加總，而非與所提供的第二運算元，即累加數C，做加總運算。

在最后的執行步驟中，調整后的加法器50會在加總運算與完成舍入運算前對接收到的IRExp進行調整，以涵蓋較大的數字范圍，例如可涵蓋FMA運算的目標數據類型的不足位與溢位指數范圍。在接收到的數值Z＝1位時，調整后的加法器50會以采取一個使IRExp遞增、而大部分均為傳統方式的方法，利用所接收到的R、S、U、O與E位來對IRVector執行舍入運算。

第二類型

如圖2所示，類型2的FMA運算80的特點在于，此運算不涉及有效減法(因此，EffSub＝0)，調整后的乘法器45被選定以執行C的累加運算(因此，Z＝1)，而相較于A和B的乘積，C的大小相當小。

因為此運算不會造成有效減法(即EffSub＝0)，累加數對準與射入邏輯220就不會在將累加數運算元尾數值C_M射入部分乘積加法器240前，對累加數運算元尾數值C_M造成與/或選擇一位反相運算。

累加數對準與射入模組220利用ExpDelta來使累加數尾數對準部分乘積，以將累加數尾數射入部分乘積加法器240。

在此將不會產生負的PNMant。此外，所產生的正的PNMant并非1’補數的減法運算的結果，因而不需端回進位校正。因此，等待中的端回進位指標E₁就會被指派為二進位數零。

因為并非一有效減法運算，此運算中將不會產生前導位的減法塊消去，因而不需執行前導位預測來預測此等消去。反之，前導位預測則可用以依據SC至PNExp的貢獻程度，來預測所需的0、1、或2位位置的標準化運算。

如同浮點運算設計的技術領域人員所能理解，A和B乘積與C的加總會產生一具有算術顯著性或比重、較乘數與被乘數的乘積大于一數位位置的溢位情形，因此需要對PNMant執行零、一或二位位置的標準化運算，來使數值對準用于本發明所描述與利用的中間結果的儲存格式。此標準化運算會產生原始尾數值GMant，而其最重要m位會成為中間結果尾數IRMant。

預標準化指數PNExp通過將輸入的乘數與被乘數指數值相加，再減去任何指數偏移值，最后再加上SC＝2，此數值于Z＝1的情況合下依據最負的ExpDelta而定。如圖2對于類型2的運算的描述可知，C的大小并不會明顯大于A和B的乘積，因此，所造成的總數會等于或大于所輸入的累加數。

因為此運算并非有效減法(即EffSub＝0)，中間結果符號IRSgn視為被乘數符號位A_S與乘數符號位B_S的XOR邏輯運算結果。

回到FMA2運算，調整后的加法器50會接收包含路徑控制信號Z的已儲存或轉送的舍入位。因為Z是二進位數一，中間結果向量IRVector只需要一些最后處理，主要就是舍入運算，即可產生最終的乘積-累加結果。在一實施例中，此調整后的加法器50將中間結果向量IRVector與一零運算元(在另一實施例中，可為一帶符號二進位數零運算元)做加總，而非與所提供的第二運算元，即累加數C，做加總運算。

在最后的執行步驟中，調整后的加法器50會對接收到的IRExp進行調整，以涵蓋較大的數字范圍，例如可涵蓋FMA運算的目標數據類型的不足位與溢位指數范圍。此調整后的加法器50會以采取一個使IRExp遞增、而大部分均為傳統方式的方法，來對IRVector執行舍入運算以產生最終的正確結果。

第三類型

如圖2所示，類型3的FMA運算85的特點在于，此運算不涉及有效減法(因此，EffSub＝0)，調整后的加法器50被選定以執行C的累加運算(因此，Z＝0)，而相較于A和B的乘積，C的大小相當大。

因此，EffSub為二進位數零。此外，路徑控制信號Z亦為二進位數零，以顯示累加數運算元的加總運算尚未執行。因為Z與EffSub均為二進位數零，等待中的端回進位指標E₁會被指派為二進位數零。

因為Z是二進位數零，累加數對準與射入邏輯220不會將乘數單元部分乘積加總數內的累加數輸入的尾數進行對準。不過，累加數對準與射入邏輯220會使此對準輸入的算術值為零。

隨后，對于部分乘積與未經舍入的非冗余數值145的完整加總運算依照傳統乘法執行單元通常采用的方法來執行，此方法不包含輸入累加數的尾數值。因為此FMA運算類并非有效減法(即EffSub＝0)，此加總運算將不會產生正的PNMant，并由SumSgn表示。此外，此正值的PNMant并非1’補數減法運算的結果，因而不需要使用端回進位校正。

因為此運算并非一有效減法運算，此運算中將不會發生前導位的減法塊消去，因而不需執行前導位預測來預測此等消去。

A和B的乘積會在乘數與被乘數的尾數乘積產生一位數位置的算術溢位。因而需要對此正的未經舍入非冗余值執行零或一位位置的標準化運算，來使此數值對準本發明所描述或使用的中間結果格式。此標準化運算會產生原始尾數值GMant，而其最重要m位會成為中間結果尾數IRMant。

因為事先確認的路徑控制信號Z為二進位數零，顯示累加運算尚未被執行，此中間結果符號IRSgn就會被視為被乘數符號位A_S與乘數符號位B_S的XOR邏輯運算結果。

回到FMA2運算，調整后的加法器50接收包含Z在內的已儲存或轉送的舍入位。因為Z為二進位數零，調整后的加法器50會使中間結果向量，即第一運算元，與累加數C，即第二運算元，做加總運算。

在執行此累加運算之前，此調整后的加法器50可調整IRExp以涵蓋較大的數字范圍，例如可涵蓋FMA運算的目標數據類型的不足位與溢位指數范圍。因為此運算是由累加數數值主導運算結果的類型3的運算85，IRExp將會比累加數輸入指數值來的小。

此運算有利于使調整后的加法器50的遠路徑加總運算的二個運算元生效。在遠路徑加總運算中，具有較小指數值的運算元的尾數于對準程序中向右移位。任何如此移位超過所需舍入位的尾數位就會被用于舍入運算。因為累加數會主導運算結果，因而可以不用提供位給舍入運算，而能簡化必要的舍入運算。

調整后的加法器50會使用由調整后的加法器50所執行的部分運算所產生的G2(如果有的話)、R₂、S₂與E₂(具有二進位數值零)舍入位，連同R₁、S₁與E₁，來對中間結果與累加數輸入值的總數進行舍入運算，以產生FMA運算的最終經舍入的正確結果，此為熟習浮點運算設計領域技術人員所能理解。

第四類型

如圖2所示，類型4的FMA運算90的特點在于，此運算涉及有效減法(因此，EffSub＝1)，調整后的乘法器45被選定以執行C的累加運算(因此，Z＝1)，而相較于A和B的乘積，C的大小相當小。

因為累加運算將會于調整后的乘法器45內執行而造成有效減法(即EffSub＝1且Z＝1)，累加數對準與射入模組220會在將累加數運算元尾數值C_M射入部分乘積加法器240前，對累加數運算元尾數值C_M造成與/或選擇一位反相運算。相對于部分乘積，此累加數對準與射入模組220會利用ExpDelta，來對準部分乘積加法器240內的累加數尾數。

因為A和B的乘積的大小明顯大于C，此運算中將不會發生前導位的減法塊消去，因而不需執行前導位預測來預測此等消去。

此外，加總程序會產生正的PNMant。因此，待定的端回進位指標E₁會被指派為二進位數一，之后會通知調整后的加法器50還需要對中間結果尾數執行端回進位校正。

如同浮點運算設計領域具有合理技術人員所能理解，PNMant可能需要依據所提供的SC至PNExp，執行零、一或二位位置的移位或標準化運算，使其對準于本發明所述或使用的中間結果所需的儲存格式。隨后，此標準化運算會選擇性地執行于此未經舍入的非冗余值，以產生原始尾數值GMant，其最重要著m位會成為中間結果尾數IRMant。

因為類型4的運算90涉及C的加總運算(即Z＝1)，而此加總運算會構成有效減法(即EffSub＝1)，在需要端回進位(即E₁為1)的情況合下產生正的PNMant，中間結果符號IRSgn會被視為被乘數符號位A_S與乘數符號位B_S的XOR邏輯運算結果。

回到FMA2運算，調整后的加法器50接收包含路徑控制信號Z在內的已儲存或轉送的舍入位。因為Z為1，中間結果向量IRVector只需一些最后處理，主要就是舍入運算，即可產生最終的乘積-累加結果。在一實施例中，此調整后的加法器50將中間結果向量IRVector與一零運算元(在另一實施例中，可為一帶符號二進位數零運算元)做加總，而非與所提供的第二運算元，即累加數C，做加總運算。

在執行零(或二進位數帶符號零)的累加運算前，調整后的加法器會調整IRExp以涵蓋較大的數字范圍，例如可涵蓋FMA運算的目標數據類型的不足位與溢位指數范圍。

響應儲存格式中間結果150內所接收的E位二進位數值，此運算需要依據第一微指令執行過程中執行的1’補數有效減法產生端回進位校正。因此，此E位連同儲存格式中間結果150的G1(如果有的話)、R₁與S₁位，做為調整后的加法器50執行單元的調整后的舍入邏輯的補充輸入。

隨后，此調整后的舍入邏輯利用G1(如果存在的話)、R₁、S₁與E₁補充輸入來計算中間結果向量與帶符號零的加總的正確舍入，以對類型4的FMA運算產生正確的運算結果。而此技術當為熟習浮點運算設計領域的技術人員所能理解。

第五類型

如圖2所示，類型5的FMA運算的特點在于，此運算涉及有效減法(因此，EffSub＝1)，調整后的加法器50被選定以執行C的累加運算(因此，Z＝0)，而相較于A和B的乘積，C的大小相當大。

因為累加運算不會于調整后的乘法器45內執行，累加數對準與射入邏輯220不會對準部分乘積加總數內的C_X，或是使此對準輸入的算術值為零。此調整后的乘法器45依據現有技術的乘法執行單元的常用方法來執行部分乘積與PNMant的完整加總運算。

因為已執行C的加總運算，此運算中將不會發生前導位的減法塊消去，因而不需執行前導位預測來預測此等消去。此外，雖然會產生正的PNMant，此數值并非1’補數減法的運算結果。因此，此運算不需要端回進位校正，而E₁會被指派為二進位數零。

如同熟習浮點運算設計領域的技術人員所能理解，PNMant可能需要依據所提供的SC至PNExp，執行零、一或二位位置的移位或標準化運算，使其對準于中間結果150所需的儲存格式。此標準化運算會產生原始尾數值GMant，其最重要m位會成為中間結果尾數IRMant。

因為類型5的運算不涉及C的加總運算(即Z＝0)，中間結果符號IRSgn會被視為被乘數符號位A_S與乘數符號位B_S的XOR邏輯運算結果。

回到FMA2運算，調整后的加法器50接收包含Z在內的已儲存或轉送的舍入位。因為Z為0，中間結果向量IRVector需要與累加數C加總以產生最終的乘積-累加運算結果。

因為類型5的運算由累加數值主導運算結果，IRExp會小于累加數輸入指數值，此運算有利于使調整后的加法器50的遠路徑加總運算的二個運算元生效。在遠路徑加總運算中，具有較小指數值的運算元的尾數于對準程序中向右移位，任何如此移位超過所需舍入位的尾數位就會被用于舍入運算。因為累加數會主導運算結果，因而可以不用提供位給舍入運算，而能簡化必要的舍入運算。

因為由儲存格式中間結果150接收的待執行端回進位指標E₁是二進位數零，因此，FMA1運算沒有留下任何待執行的端回進位校正。是以，E₁位連同儲存格式中間結果150的R₁與S₁位，以及G1位(如果存在的話)，做為調整后的加法器50執行單元的調整后的舍入位的補充輸入。

然而，由調整后的加法器50所執行的累加運算可能會另外導致1’補數有效減法的產生。如此，調整后的舍入邏輯即可產生包含端回進位在內的舍入位，來計算出中間結果向量與累加器輸入值的加總的正確舍入值，以產生FMA運算的正確結果。而此技術當為熟習浮點運算設計領域的技術人員所能理解。

特定微指令

在本發明的另一個面向中，轉譯器與/或微碼只讀存儲器(ROM)20用以將FMA指令轉譯或轉換為第一與第二特定微指令，分別由乘法與加法單元執行。舉例來說，第一(或更多)特定微指令可以在一類似于將傳統乘法單元進行最小限度的調整，以符合所述目的的乘法執行單元內執行。而第二(或更多)特定微指令可以在一類似于將傳統家法單元進行最小限度的調整，以符合所述目的的加法執行單元內執行。

圖11顯示本發明將融合FMA指令535通過FMA指令轉譯或轉換，產生第一與第二特定微指令553與571的一實施例。就一未受限的范例而言，此融合FMA指令535包含一指令操作碼欄538、一目標欄541、一第一運算元(被乘數)欄544、一第二運算元(乘數)欄547、與一第三運算元(累加數)欄550。

依據操作碼欄538的指示，此FMA運算可為一乘-加(multiply-add)、一乘-減(multiply-subtract)、一負乘-加(negative multiply-add)、或一負乘-減(negative multiply-subtract)指令。如同存在許多不同類型的FMA指令535，也會存在許多類型的第一特定微指令553，如乘-加、乘-減、負乘-加、或負乘-減微指令。這些類型的特征，如果有的話，會反映在相關的微指令553的操作碼欄556中。

第一特定微指令553會引導第一至第五類型的FMA運算所需的部分算術運算的實行。依據類型的不同，第一特定微指令553所執行的特殊運算亦有差異。第一特定微指令553分配給第一執行單元，例如前文所述的調整后的乘法器45。

第二特定微指令571會引導第一至第五類型的FMA運算所需的剩余算術運算的實行。依據類型的不同，第二特定微指令571所執行的特殊運算亦有差異。在本實施例中，第二特定微指令571分配給第二執行單元，例如前文所述的調整后的加法器50。為了方便浮點乘-加融合運算或浮點乘-減融合運算的實行，此第二特定微指令571可具有一子類型，例如加或減。

尤其是，此第一特定微指令553會將第一、第二與第三輸入運算元544、547與550，分別特定為被乘數運算元A、乘數運算元B與累加數運算元C。此第一特定微指令還可以特定一目標欄559，指向暫時暫存器。又或者，此目標暫存器559可為隱含者。

第一特定微指令553會引導FMA1子運算執行，即A和B的部分乘積與在某些條件下與C的加總，以產生未經舍入的儲存格式中間結果150。此第一特定微指令553也會引導變數EffSub與ExpDelta的確認動作，借以對一組預先確定的EffSub與ExpDelta值，產生指派給Z位的數值二進位數一。此數值會依序控制許多相關程序。

二進位數一的Z位指出此對累加數位的加總運算將會于第一運算中執行，而不須由第二微指令來執行。隨后，此Z位的指定與ExpDelta會用于使部分乘積加法器240內被選擇性互補累加數尾數進行對準，此部分乘積加法器240經適當調整使能接收此額外事項。

第一特定微指令553并引導一完整加總運算對此未經舍入的非冗余值(PNMant)執行。此完整加總運算依據傳統乘法執行單元的通常方法，但在部分乘積的加總運算中，納入額外的選擇性位反相、已對準的累加數輸入值C_M或若是PNum為負，此條件就會由信號SumSgn表示。

第一特定微指令553并引導PNMant的移位與位反相運算，以產生一原始尾數值(GMant)，接下來會執行GMant的縮減以產生儲存格式中間結果150的中間結果尾數(IMant)。因此，此中間結果尾數IMant會是此EffSub指定的運算所產生的1’補數算術差的標準化絕對值，但不執行任何端回進位校正。

第一特定微指令553并引導中間結果指數值的運算。首先依據Z為二進位數一時，ExpDelta的最負值，產生一預標準化指數值(PNExp)，其數值等于被乘數指數A_E與乘數指數B_E的加總、減去指數偏移值ExpBias、再加上一移位常數SC。然后，從PNExp的數值減去由標準化移位器130執行的尾數標準化運算所占據的量，以產生中間結果指數值(IRExp)。

第一特定微指令553并引導中間結果符號IRSgn的運算。此中間結果符號IRSgn，連同中間結果尾數IRMant與中間結果指數IRExp，構成儲存格式中間結果150的向量IRVector。

第一特定微指令553并會產生包含Z在內的許多舍入位。GMant未納入中間結果尾數的最不重要位會被縮減至由舍入(R)與粘(S)位表示，而在一實施例中，還包含保護(G)位。若是部分乘積加法器240已經將C與A和B的乘積累加，并且此運算是產生一正的PNMant值的一有效減法而，端回進位(end-around-carry bit)E就會被指派為二進位數一，以顯示需要執行端回進位。此第一特定微指令并會使中間不足位(U)與中間溢位(O)位被確認。

最后，在一實施例中，第一特定微指令553會使儲存格式中間結果150向量IRVector儲存于存儲器，在另一實施例會使其轉送，而在又一實施例，則會使其同時儲存與轉送。相同地，在一實施例中，第一特定微指令553會使舍入位儲存于存儲器，在另一實施例中會使其轉送，而在又一實施例中，則會使其同時儲存與轉送。如此可使負責執行第一特定微指令的執行單元，在執行第一FMA微指令后而在執行第二微指令前，執行其他與FMA運算無關的運算。

第二特定微指令571提供一操作碼574并分別特定第一與第二輸入加法器運算元580與583。第二特定微指令571會促使FMA2運算執行。若是C的累加并非由第一特定微指令553造成，此運算還包含C與中間結果尾數的條件累加。第二特定微指令571并會產生FMA運算的最終舍入后結果。

第一累加數運算元580將第一特定微指令553所產生的乘積作為其數值，第二累加數運算元583將第一特定微指令所指定的相同累加數值作為其數值。在一實施例中，第二特定微指令571的源運算元欄580指向與第一特定微指令553的目標欄599相同的暫存器。第二特定微指令571并特定一目標暫存器577，在一實施例中，此目標暫存器與FMA指令535的目標欄541為同一個暫存器。

結論

雖然此實施方式在有效減法時提供1’補數的累加運算，熟習算術或浮點運算設計領域的技術人員當可理解，在另一實施方式中，在有效減法時利用本發明的方法來使用2’補數的累加運算。

本發明具有許多優點。本發明相容于IEEE，并提供其他實施方式明顯無法提供的校正給所需的FMA算術結果，尤其是響應IEEE舍入運算的要求。

本發明通過維持可分別取用的乘法器與加法器單元，最大化供指令分配的各自獨立算術功能單元的可用性，而讓計算機處理器在一定實施成本下，可以更充分地開發指令平行處理。換言之，本發明讓最少的硬件達到最大可能性的同步利用，使其能以最快速度完成預期中最頻繁的運算，此處理方式可改善算數運算結果的產出。通過將所需的特定類型的第一與第二(或更多)微指令進行分配，并使其以暫時性與/或物理性各自獨立的方式分別執行，因此，雖然此等用于FMA的第一微指令會被分配至乘法功能單元執行，第二或其他更多無關的微指令則可同時被分配至一個或多個加法功能單元。

同樣地，雖然此等用于FMA的第二微指令會配分配至功能方塊單元，任何需要乘法功能的其他無關的微指令則可同時被分配至乘法功能單元。

如此，依據所需的整體效能與所需的系統指令平行處理能力，所提供的乘法與加法功能單元的數量可更具彈性。因而相較于一個整體的FMA硬件，可減少每個功能單元的設置成本。計算機系統重排微指令的能力也會提升，而能降低成本與功耗。

相較于其他設計，本發明不需要使用大型或特殊目的的硬件即可減少指令延遲。其他FMA硬件實施的設計都需要使用大型與復雜的電路功能，如先行標準化運算(anticipatory normalization)、先行加法運算、先行符號運算、與復雜的舍入電路。這些復雜元件常常會成為最終設計中關鍵的耗時路徑、會在運算過程中消耗額外的能量、并在物理上會占據電路設置空間。

本發明不需在大型的FMA硬件內設置特殊旁路電路或模態以減少如現有技術所提供的簡單加法或乘法指令的延遲。

本發明的其他實施方式，可在特殊類型的第一微指令的執行過程，執行或多或少的算術運算，可在特殊類型的第二微指令的執行過程，執行或多或少的算術運算。亦即配置給這些微指令的運算可為不同。如此，其他這些實施方式可對任一/任何需要的獨立運算單元進行或多或少的調整。如此，這些其他實施方式可儲存或多或少的中間結果于舍入快取內，并可將或多或少的中間結果轉送至第二為指令。

其他實施方式中，所述的舍入快取可為可定址暫存器位、內容可存取存儲器、佇列儲存空間、或對映功能。

其他實施方式可提供多個獨立的硬件或執行單元來執行第一微指令，與/或提供多個獨立的硬件或執行單元來執行第二微指令。同樣地，如果有利的話，這些實施方式也可以提供多個舍入快取給不同的源碼指令流或數據流、或是多核計算機處理器的各種實施方式。

此實施方式用于超純量、非循序指令分配，不過其他實施方式亦可用于依序指令分配的情形，例如，通過從指令快取移除以及提供至數據轉送網路的過程，可將指令從所提供的乘法運算單元分配至獨立的加法運算單元。本發明對于FMA運算分類的例示，以及本發明提及的所需最少量硬件調整，在依序指令分配的應用中，亦有其優點。雖然本說明書將FMA運算區分為五個類型，不過其他劃分方式，無論是較少、較多、與/或使用不同類型，均屬本發明的范疇。

此外，雖然本說明書中已描述不同的調整后的乘法與加法單元以執行FMA運算，在本發明的一實施例中，亦可使用一乘積-累加單元響應第一乘積-累加指令來執行第一乘積-累加子運算，并將其結果儲存至外部儲存空間，而此乘積-累加單元會再響應第二乘積-累加指令來執行第二乘積-累加子運算。

本發明可用于FA_M運算的單指令流多數據(SIMD)實施方式，此等方式有時會被稱為向量指令類型或向量FMA運算。并且此方式會有多個調整后的乘法器的實例與多個調整后的加法器的實例。在一實施例中，本發明使用單一舍入快取來配合一個SIMD應用的需求。而在另一實施例中，則可使用多個舍入快取來配合多個SIMD應用的需求。

雖然本發明關于需要一乘法運算連同后續加法或累加運算的浮點融合乘法加法運算，不過，本發明所提供的方法亦可用于其他實施方式，尤其是針對某些中間結果使用快取的技術、針對需要兩個以上連鎖(chained)的算術運算的計算、針對不同算術運算、或以不同順序執行這些算術運算。舉例來說，某些時候可能需要將這些方法應用于其他算術運算的混合(即，涉及兩個以上的算術操作子或三個以上的運算元的算術運算)，例如連鎖的乘法-乘法-加法運算或乘法-加法-加法運算，以提升算術準確性或提升運算產出。此外，從其他面向來看，本發明亦可應用于整數算術運算。舉例來說，舍入至特定位位置的整數運算可區分為第一與第二子運算，其中第一子運算產生一未經舍入的中間結果，而第二子運算由此未經舍入的中間結果產生一經舍入的最終結果。依此，在需要時，其他實施方式可將不同的狀態位記錄于快取機制內。

本說明書關于舍入位與其他內部位的描述為利于說明本發明的精神，本發明當可用于其他類型的指標，包含舍入運算相關或運算控制相關的變數的不同編碼表現形式。此外，針對說明書中將變數描述為具有“二進位數一＂(也就是邏輯一)的許多段落，此描述包含具有“二進位數零”(也就是邏輯零)的變數的等效布林實施方式，并包含這些變數的其他表示方式。相同地，針對說明書中將變數描述為具有“二進位數零＂(也就是邏輯零)的許多段落，此描述包含具有“二進位數一”(也就是邏輯一)的變數的等效布林實施方式，并包含這些變數的其他表示方式。此外，依據本說明書當可理解，在本文中，累加包含加法加總與加法差的情形。

此外，依據本說明書當可理解，在本文中，指令包含架構指令與可由架構指令轉譯或轉換產生的微指令。同樣地，指令執行單元并非僅限于微處理器直接執行架構指令而未預先將其轉譯為微指令的情形。由于微指令亦屬指令的一種類型，因此，指令執行單元也會包含微處理器先將指令集架構指令轉譯或轉換為微指令，而指令執行單元總是只執行微指令的情形。

在本說明書中，尾數與有效位數的用語可互用。其他如原始結果與中間結果的用語，為區分在FMA運算的不同階段所產生的結果與表示方式。此外，在本說明書中，儲存格式中間結果的用語包含一中間結果向量(意指一數的量)與多個運算控制變數。這些用語不應被僵化或狹隘地解釋，而應依據申請人所表現出來的目的探究其實質，而理解這些用語依據前后文的不同可能指涉不同的事件。

圖1、3-6中的功能方塊可描述為模組、電路、子電路、邏輯、與其他數位邏輯與微處理器設計的技術領域中常用于指稱由線路、電晶體與/或其他執行一個或多個功能的物理結構所構成的數字邏輯用語。本發明亦可涵蓋將說明書所描述功能以不同于說明書所描述的方式分派的其他替代實施方式。

下列參考文獻納入本申請以說明FMA設計的相關概念與并使本申請發明能為讀者理解。

參考文獻：

Hokenek,Montoye,Cook,"Second-Generation RISC Floating Point with MultiplyAdd Fused",IEEE Journal Of Solid-State Circuits,Vol 25,No 5,Oct1990.

Lang,Bruguera,"Floating-Point Multiply-Add-Fused with Reduced Latency",IEEE Trans On Computers,Vol 53,No 8,Aug 2004.

Bruguera,Lang,"Floating-Point Fused Multiply-Add:Reduced Latency for FloatingPoint Addition",Pub TBD-Exact Title Important.

Vangal,Hoskote,Borkar,Alvanpour,"A 6.2-GFlops Floating-Point MultiplyAccumulator With Conditional Normalization",IEEE Jour.Of Solid-State Circuits,Vol 41,No 10,Oct 2006.

Galal,Horowitz,"Energy-Efficient Floating-Point Unit Design",IEEE Trans On Computers Vol 60,No 7,July 2011.

Srinivasan,Bhudiya,Ramanarayanan,Babu,Jacob,Mathew,Krishnamurthy,Erraguntla,"Split-path Fused Floating Point Multiply Accumulate(FPMAC)",2013Symp on Computer Arithmetic(paper).

Srinivasan,Bhudiya,Ramanarayanan,Babu,Jacob,Mathew,Krishnamurthy,Erraguntla,"Split-path Fused Floating Point Multiply Accumulate(FPMAC)",2014Symp on Computer Arithmetic,Austin TX,(slides from www.arithsymposium.org).

Srinivasan,Bhudiya,Ramanarayanan,Babu,Jacob,Mathew,Krishnamurthy,Erraguntla,United States Patent 8,577,948(B2),Nov 5,2013.

Quach,Flynn,"Suggestions For Implementing A Fast IEEE Multiply-Add-Fused Instruction",(Stanford)Technical Report CSL-TR-91-483July,1991.

Seidel,"Multiple Path IEEE Floating-Point Fused Multiply-Add",IEEE2004.

Huang,Shen,Dai,Wang,"A New Architecture For Multiple-Precision FloatingPoint Multiply-Add Fused Unit Design",Pub TBD,Nat'l University of Defense Tech,China(after)2006.

Paidimarri,Cevrero,Brisk,Ienne,"FPGA Implementation of a Single-Precision Floating-Point Multiply-Accumulator with Single-Cycle Accumulation",Pub TBD.

Henry,Elliott,Parks,"X87 Fused Multiply-Add Instruction",United States Patent 7,917,568(B2),Mar 29,2011.

Walaa Abd El Aziz Ibrahim,"Binary Floating Point Fused Multiply Add Unit",Thesis Submitted to Cairo University,Giza,Egypt,2012(retr from Google).

Quinell,"Floating-Point Fused Multiply-Add Architectures",Dissertation Presented to Univ Texas at Austin,May 2007,(retr from Google).

Author Unknown,"AMD Athlon Processor Floating Point Capability",AMD White Paper Aug 28,2000.

Cornea,Harrison,Tang,"Intel Itanium Floating-Point Architecture"Pub TBD.

Gerwig,Wetter,Schwarz,Haess,Krygowski,Fleischer,Kroener,"The IBM eServer z990 floating-point unit",IBM Jour Res&Dev Vol 48 No 3/4 May,July2004.

Wait,"IBM PowerPC 440 FPU with complex-arithmetic extensions",IBM Jour Res&Dev Vol 49 No 2/3 March,May 2005.

Chatterjee,Bachega,et al,"Design and exploitation of a high-performance SIMD floating-point unit for Blue Gene/L",IBM Jour Res&Dev,Vol 49 No 2/3March,May 2005.