一種互聯發電系統的可靠性評估方法與流程

文檔序號：11134837閱讀：465來源：國知局

本發明屬于電力系統的可靠性分析技術領域，具體是針對負荷預測不確定性問題而提出的一種基于通用生成函數的電力不足概率分析方法。

背景技術：

發電系統可靠性是指統一并網運行的全部發電機組按照可接受的標準及期望數量來滿足電力系統負荷電力或電量需求能力的度量。在發電系統可靠性評估中，通常把孤立系統和互聯系統分開來研究。孤立系統又稱單母線系統或單地區系統，通常假定任意電源的可用發電容量都能夠不受限制地傳輸到任意負荷點上，即電源和負荷之間的輸電線路是完全可靠的。互聯系統是指用具有一定輸送能力的聯絡線把兩個或多個彼此獨立的發電系統聯接起來的系統，又稱多區域發電系統，被聯接的各區域都是一個單母線系統。由于彼此獨立的單母線系統的負荷特征和機組的故障參數各不相同，通過互聯可以實現發電容量的相互支援，既能提高各獨立系統的可靠性，又提高了經濟性。因此，電力系統之間的互聯越來越普遍，且互聯規模也日益增大。

當前,電力不足概率法(Loss of Load Probability Method,LOLP)是互聯系統可靠性定量評估中應用最廣泛的方法，該方法于1947年由Calabrese提出，Kirchmayer等隨后將其拓展至互聯系統。LOLP法把發電系統的停運容量概率模型和系統的日尖峰負荷曲線(或持續曲線)綜合起來，得到日(或小時)尖峰負荷超過系統可用發電容量的概率，記為LOLP。計算互聯系統的LOLP指標一般采用兩種方法：二維概率陣列法和支援容量概率表法。二維概率陣列法是根據各系統的裕度容量概率表和聯絡線的容量限制形成互聯系統的裕度容量狀態矩陣，再按一定的規則將該狀態矩陣分成若干塊，從而估計各個子系統和互聯系統的可靠性指標。支援容量概率表法主要根據系統的停運容量概率表、可用備用容量、聯絡線允許傳輸容量和支援合同形成一個系統對另一個系統的支援容量概率表，即在研究另一個系統的可靠性時，把該系統作為一個等效多臺發電機組來處理。其中，二維概率陣列法適用于兩地區互聯，而支援容量概率法較之更為靈活，可用于研究多區域互聯。

LOLP是以日負荷模型和發電機組的故障狀態模型為基礎的，但二維概率陣列法和支援容量概率表法所采用的負荷模型指所研究期間內確切的日尖峰負荷值，是根據歷史數據預測獲得的，具有不確定性。因此，需要一種在考慮負荷預測不確定性的前提下研究互聯發電系統LOLP指標的新方法。

技術實現要素：

本發明的目的是為了解決互聯發電系統可靠性評估中的負荷預測不確定性問題，提出了一種基于通用生成函數(Universal Generating Function,UGF)的電力不足概率(LOLP)法。

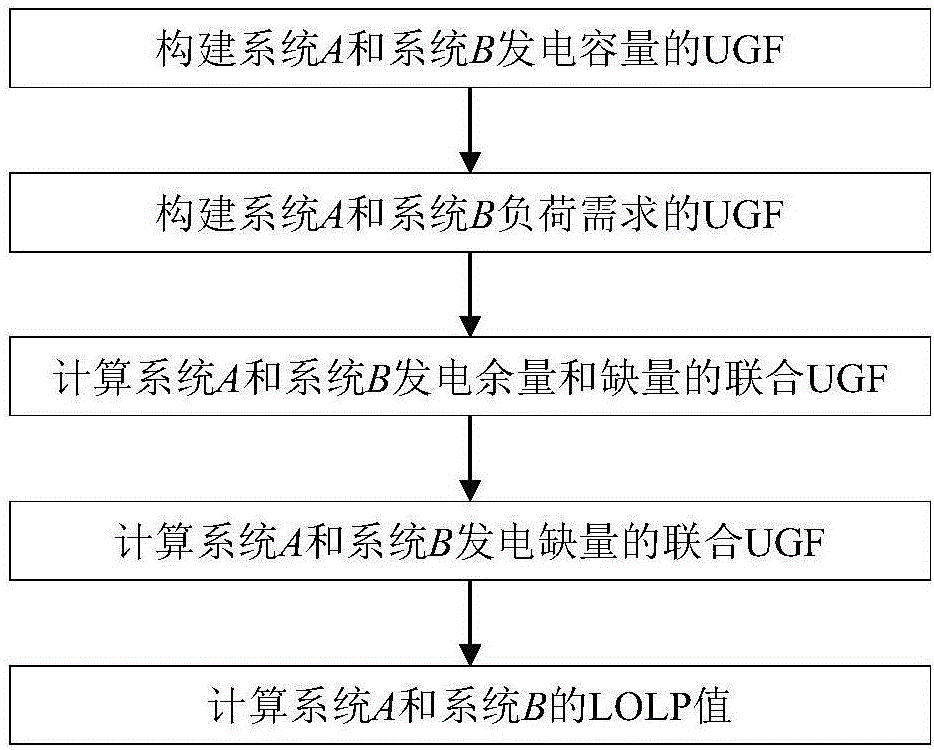
本發明的技術方案是：一種基于UGF的LOLP法，包括如下步驟：

步驟1：將裝有多臺機組的發電系統等效為由若干部件組成的多狀態系統，再構建系統發電容量的UGF；

步驟2：考慮負荷預測的不確定性后，得到各系統負荷需求的UGF；

步驟3：計算各系統發電余量和缺量的聯合UGF；

步驟4：根據系統間聯絡線所允許的最大傳輸容量，寫出實現容量支援后各系統發電缺量的聯合UGF；

步驟5：根據步驟4中得到的UGF，得到各系統的LOLP值。

進一步地，所述步驟1可分為如下三步：

第一步：作系統等效處理：

所研究的發電系統都裝有若干個機組，且具有有限個離散的發電容量狀態(比如：0MW、50MW、100MW)，故可將機組看作部件，進一步將各發電系統等效成由若干部件組成的多狀態系統。而用具有一定輸送能力的聯絡線將兩個或多個多狀態系統聯接起來，即為互聯。本發明所提出的方法是以互聯結構中的多狀態系統為研究對象的，以下簡稱為系統；

第二步：對于具有k個狀態的機組e，其發電容量的UGF如下所示：

式中，p_(e,i)和w_(e,i)分別表示機組e處于第i個狀態的概率和發電容量，z本身不具有任何實際意義；

第三步：假定系統j是由n臺機組(部件)組成，且系統發電容量為那么可通過組合算子遞歸運算得到系統j發電容量的UGF如下所示：

式中，p_(j,k)＝Pr{W_j＝w_(j,k)}。φ(·)為系統結構函數，表示系統狀態性能由系統結構及所有部件狀態屬性共同決定。特別地，對任意串聯的部件x和y，其組成系統的結構函數可表示為：

φ(w_x,w_y)＝min(w_x,w_y) (3)

對任意并聯的部件x和y，其組成系統的結構函數可表示為：

φ(w_x,w_y)＝w_x+w_y (4)

進一步地，所述步驟2的計算過程可分為如下兩步：

第一步：描述負荷預測的不確定性：

負荷實際值與預測值的誤差是一個隨機過程，通常使用正態分布來描述，即誤差服從正態分布，正態分布的數學期望就是預測的峰值負荷，標準差σ＝0.02；

第二步：若系統j的負荷需求為寫出其UGF如下所示：

式中，q_(j,m)＝Pr{L_j＝l_(j,m)}。

進一步地，所述步驟3的計算過程具體闡述如下：

由于系統j的發電容量W_j和負荷需求L_j是兩個互相獨立的離散隨機變量，它們的任何函數運算結果亦是離散隨機變量，并且可通過通用生成函數的組合運算得到。定義系統j的發電余量為S_j＝max(W_j-L_j,0)、缺量為D_j＝max(L_j-W_j,0)，顯然S_j和D_j也是離散隨機變量。那么，可以定義一個組合算子來計算系統j發電余量和缺量的聯合UGF如下所示：

式中，π_(j,f)＝Pr{S_j＝s_(j,f)∩D_j＝d_(j,f)}，α(·)為系統j發電余量函數，β(·)為系統j發電缺量函數。特別地，對系統任意發電容量w_k和負荷需求l_m，其發電余量函數和缺量函數分別表示為：

α(w_k,l_m)＝max(0,w_k-l_m) (7)

β(w_k,l_m)＝max(0,l_m-w_k) (8)

進一步地，所述步驟4的計算過程具體闡述如下：

假定任意兩個多狀態系統間有一條可實現雙向輸送、最大輸送能力為c的聯絡線，且聯絡線的可用度為1，其UGF可記為：

η(z)＝z^c (9)

計算實現容量互相支援后系統j的發電缺量如下：

D_j′＝D_j-min(D_j,S_Ω,c) (10)

式中，D_j和D_j′分別表示系統j實現容量支援前后的發電缺量，S_Ω表示互聯結構中的所有系統發電余量之和。

那么，可以定義一個組合算子來描述各系統經過容量支援后發電缺量的聯合UGF如下所示：

式中，π′_f＝Pr{D₁′＝d₍′_1,f)∩D₂′＝d₍′_2,f)}，v是組成互聯結構的系統個數，μ(·)為系統實現容量支援后的發電缺量函數。特別地，對互聯結構中的任意系統j，實現容量支援后的發電缺量函數可表示為：

μ(d_j,s_Ω,c)＝d_j-min(d_j,s_Ω,c) (12)

進一步地，所述步驟5的計算過程具體闡述如下：

根據電力不足概率的定義可知，系統的LOLP值是指峰值負荷超過系統可用發電容量的概率，即系統發電容量的缺量不為0的概率，記為

LOLP_j＝1-Pr{D_j′＝0} (13)

由此可得到系統互聯時考慮負荷預測不確定性后的電力不足概率。

本發明的有益效果：由于考慮了負荷預測的不確定性，本發明中使用正態分布合理地描述了這種不確定性，從而將系統的負荷需求簡化為一個離散隨機變量，進一步使用了通用生成函數簡潔、高效地得到了系統互聯后的電力不足概率值。

附圖說明

圖1為本發明提出的一種互聯發電系統的可靠性評估方法的主流程圖；

圖2為本發明實施例中A、B系統互聯的結構示意圖；

圖3為本發明實施例中系統A發電容量的UGF對應表圖；

圖4為本發明實施例中系統B發電容量的UGF對應表圖；

圖5為本發明實施例中系統A的預測負荷誤差分布圖；

圖6為本發明實施例中系統A的峰荷分布概率表圖；

圖7為本發明實施例中系統B的預測負荷誤差分布圖；

圖8為本發明實施例中考慮負荷預測不確定性后A、B系統負荷需求的UGF對應表圖。

具體實施方式

為了使本發明的目的、技術方案及優點更加明了，以下通過具體的實施例對本發明作進一步地闡述。如附圖2所示的互聯發電系統，A系統共裝五臺10MW及一臺25MW的機組，總容量為75MW；B系統共裝四臺10MW及一臺25MW的機組，總容量為60MW。假定每臺機組的強迫停運率為0.02，兩系統之間有一條輸送能力為10MW的聯絡線，且假定聯絡線的可用度為1。系統A的峰荷是50MW，系統B的峰荷是40MW。對各系統進行可靠性評估，其步驟包括：

步驟1：計算系統A和系統B發電容量的UGF。

通用生成函數(UGF)是一種簡潔、高效的離散隨機變量組合運算工具，最早由Ushakov于1987年提出，隨后被Lisnianski和Levitin廣泛地應用于解決多狀態系統性能及可靠性評估問題中。其基本思想是將離散隨機變量表示為多項式形式，根據離散隨機變量的運算法則定義多項式的組合算子，并通過遞歸運算可得到最終結果的離散隨機變量的多項式形式。由于通用生成函數在處理離散隨機變量運算上的優勢。因此，它也被應用于結構可靠性分析。本發明就是使用通用生成函數來計算考慮負荷預測不確定性的互聯發電系統的電力不足概率。

首先，根據每臺機組的強迫停運率為0.02，寫出各機組發電容量的UGF如下所示：

ω_(1,1)(z)＝0.98z²⁵+0.02z⁰

ω_(1,2)(z)＝0.98z¹⁰+0.02z⁰

ω_(2,1)(z)＝0.98z²⁰+0.02z⁰

ω_(2,2)(z)＝0.98z¹⁰+0.02z⁰

其中，ω_(1,1)(z)和ω_(1,2)(z)分別表示組成系統A的兩類機組發電容量的UGF，ω_(2,1)(z)和ω_(2,2)(z)分別表示組成系統B的兩類機組發電容量的UGF。

再由式(2)計算得到系統A和系統B的UGF，其中發電容量的狀態概率值取八位小數，概率低于10^-8的狀態忽略不計，可得結果如附圖3和附圖4所示。

步驟2：計算系統A和系統B負荷需求的UGF。

首先，用正態分布來描述系統預測負荷的不確定性。按照給定的條件，系統A峰荷實際值與預測值的誤差服從均值為50MW、標準差σ＝0.02×50＝1MW的正態分布，將該分布劃分為七個離散型的等級區間，得到預測負荷誤差分布如附圖5所示，取標準差等于±1、±2、±3算出每個等級區間對應峰值負荷的大小，其存在概率即該等級區間的面積，從而可以得到考慮負荷預測的不確定性后的負荷概率分布表圖，如附圖6所示。同理，可以得到系統B預測負荷誤差分布如附圖7所示。

再按照式(5)寫出系統A和系統B負荷需求的UGF，結果如附圖8所示。

步驟3：按照式(6)計算各系統發電余量和缺量的聯合UGF。

步驟4：假定系統間聯絡線的可用率為1，為了后續數據便于統計和整理，對于兩系統互聯的情況，可將式(11)記為

U(z)＝π₁′z^(0,0)+π₂′z^(0,1)+π₃′z^(1,0)+π₄′z^(1,1)

其中，π₁′＝Pr{D₁′＝0∩D₂′＝0}，π₂′＝Pr{D₁′＝0∩D₂′>0}，π₃′＝Pr{D₁′>0∩D₂′＝0}，π₄′＝Pr{D₁′>0∩D₂′>0}。