一種基于MoCD算法的商品配送路徑規劃方法與流程

本發明涉及一種物流系統中的商品配送路徑規劃算法，具體涉及一種基于MoCD算法(基于Dijkstra算法的多目標約束算法)的商品配送路徑規劃方法。
背景技術：
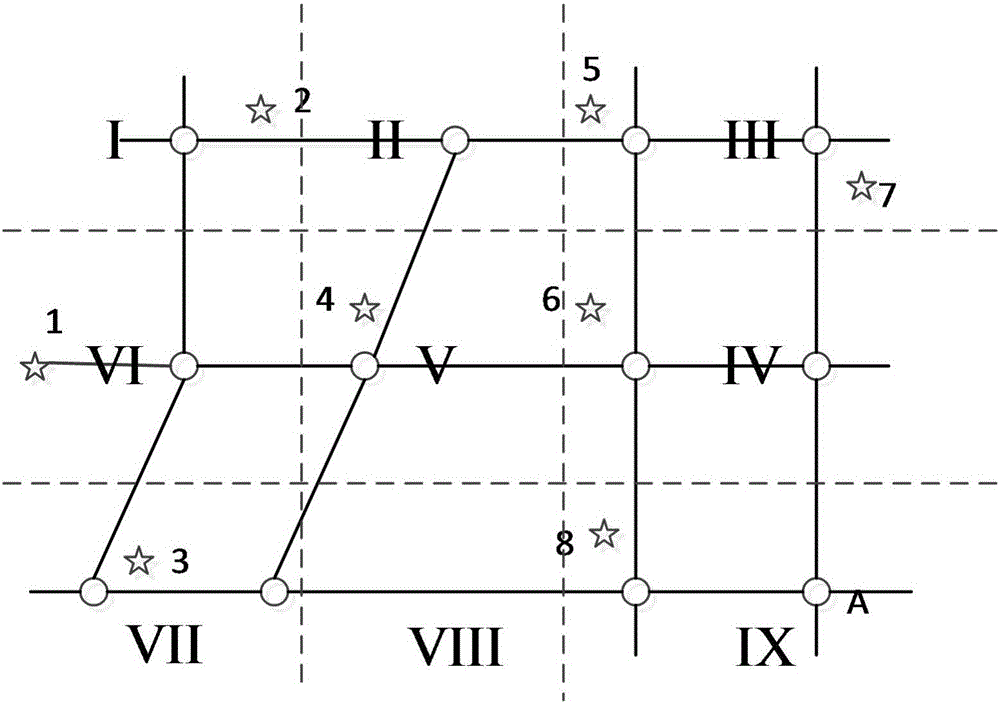
：近些年來，隨著互聯網的快速發展，電子商務已經滲透到各行各業當中，隨之而來的現代物流業正成為新的研究熱點。作為現代物流管理中的一個核心環節，商品配送引起了專家學者們的廣泛研究與關注，商品配送的技術水平和整體效率也得到了較大程度的提高。商品配送中的路徑規劃，是物流系統中的關鍵環節。較好的商品規劃路徑方案，有利于加快物流響應速度，提高服務質量，降低物流成本，提高效率以及增加經濟效益。目前，物流系統中的商品配送路徑規劃主要靠車載的導航系統，根據車輛地理位置和目的地地理位置，由導航系統中的地圖給車輛指引路線。國內外已經有很多的專家學者給出了路徑規劃的算法，其中主要有傳統的啟發式算法和人工智能算法。但這些算法大都只給出了最短路徑的規劃方案，并沒有考慮車輛的商品發往的目的地、需求數量、價格以及商品裝載的難易程度等。若某地區有較多商品廠家，當車輛向不同地點配送商品時，如何找到滿足車輛需求的廠家的最優路徑規劃方案成為當前面臨的問題。因此，該研究內容具有重要的研究價值。為了解現有技術的發展狀況，對已有的論文和專利進行了檢索、比較和分析，篩選出如下與本發明相關度比較高的技術信息：技術方案1：專利號為CN104616070A的《一種物流配送路徑規劃方法及裝置》的專利，涉及一種物流配送路徑規劃方法及裝置，主要通過五步完成：第一，獲取每個需求點的配送量和配送點與需求點之間以及各需求點之間的直接可達最短路徑的距離；第二，以配送點和需求點作為節點，以所述配送點與需求點之間以及各需求點之間直接可達最短路徑作為邊，構造路徑連通圖；第三，根據所述每個需求點節點的配送量以及每條邊的距離劃分所包含節點的總配送量不大于預設運量容限的任務子圖；第四，構造包含任務子圖中所包含的全部節點的最小支撐樹；第五，從所述最小支撐樹與所述配送點節點構成回路中選取包含最小支撐樹路徑最長的回路作為配送路徑主干，所述配送路徑主干之外的懸掛節點采用往返路徑，得到該任務子圖的配送路徑。該發明采用自組織方式合理將需求點進行鄰近合并劃分任務子圖，適用于大規模的配送路徑規劃。技術方案2：專利號為CN103383756A的《一種煙草物流配送路徑規劃方法》的專利，屬于煙草配送領域，涉及一種煙草物流配送路徑規劃的方法，主要通過四步來完成：第一，對該地區內的所有零售戶利用自下而上的一階段方法和直接指派的方法進行聚類，其中自下而上的一階段方法包括：初始狀態的每個零售點都是一個類，若類的容量沒有達到上限，鄰近的類相互聚合，直到沒有類可以再聚合，直接指派的方法包括：初始階段指定類的數目，并指定每個類的初始核，若類的容量沒有達到上限，將每個零售點向最接近的類聚合，并更新類的核，直到所有點都已聚合到相應的類；第二，基于離散模型的站點與服務區規劃，將整個配送地區均分為一定數量的點陣，然后給定站點數目，以最小化總里程為目標，采用數學模型計算最佳的選址方案；第三，基于配送工作量模型的最優路徑確定，主要考慮了綜合作業時間，采用Dijkstra算法計算最優路徑；第四，訂單日規劃，根據總體工作量需求，確定車輛數目范圍，以工作量均衡為目標，確定最佳的規劃方案。技術方案3：專利號為CN103413209A的《多客戶多倉庫物流配送路徑選擇方法》的專利，涉及一種配送路徑選擇方法，主要通過八步完成：第一，蟻群優化方法初始化；第二，路徑構建；第三，信息素構建；第四，禁忌搜索方法初始化；第五，構建鄰域路徑集；第六，評價鄰域路徑集；第七，路徑更新；第八，更新禁忌表。該發明能夠適應于多倉庫的物流配送的路徑優化處理。技術方案1采用了構造節點的最小支撐樹的方法，首先獲取每個需求點的配送量和配送點與需求點之間以及各需求點之間的直接可達最短路徑的距離，然后以配送點和需求點為節點，在配送點和需求點及需求點之間直接可達最短路徑為邊，構造路徑連通圖,進而根據每個需求點節點的配送量以及每條邊的距離對所述路徑連通圖劃分任務子圖，在任務子圖中構造最小支撐樹，選取包含最小支撐樹的最長路徑作為主干配送路徑，其他節點采用往返路徑，得到任務子圖的配送路徑，并在特定的情況下進行路徑的優化。在實際應用場景下，該方法需要統計各節點的需求信息，適合統一管理的情況下的較大規模的配送路徑規劃，但在非統一管理的場景下靈活性較差，普適性不強；技術方案2涉及煙草的配送領域，首先對所有零售戶進行聚類，接著將配送地區劃分點陣，根據數學模型計算最佳的配送點選址方案，然后根據訂單日的工作量確定車輛數目范圍，確定配送路徑。該方案根據煙草零售戶的較分散特點，采取該方式的煙草物流配送路徑規劃，能解決煙草的不同供需量情況下配送路徑規劃，但該方案方法復雜，算法的復雜性較高，在要求實時路徑規劃時效率較低；技術方案3采用了蟻群優化的方法進行配送路徑的優化，首先利用蟻群算法構建路徑，然后對所建立的路徑進行評價、更新，并結合禁忌搜索優化方法對路徑進行優化，最終得到配送車輛從出發到配送完貨物后返回出發地點的最優路徑。該方法能適應多客戶多倉庫物流配送路徑的規劃，可以得到較好的路徑規劃。但該方案計算開銷很大，搜索時間較長，在實際應用中對處理器的要求較高，理論意義較大，實用性不強。技術實現要素：為解決上述現有技術中的不足，本發明的目的是提供一種基于MoCD算法的商品配送路徑規劃方法，通過規劃最優路徑，達到節約運輸成本、提高車輛裝載率以及提高配送的效率的目的。本發明的目的是采用下述技術方案實現的：本發明提供一種基于MoCD算法的商品配送路徑規劃方法，其改進之處在于，所述方法包括下述步驟：步驟101：建立城市道路網模型；步驟102：確定商品價格信息；步驟103：根據不同廠家商品的配送目的地，篩選符合要求目的地的廠家；步驟104：確定商品供需方案；步驟105：利用Dijkstra算法對車輛到商品廠家的路徑進行規劃；步驟106：采用逐級搜索方式對城市道路網模型劃分區域進行搜索；步驟107：輸出最優路徑規劃方案，結束。進一步的，所述步驟101中，定義一條城市道路的交叉點或端點作為城市道路網的節點，節點有相對的經度、緯度地理坐標；兩節點間的路段定義為城市道路網的邊，路段的距離定義為邊的權值；根據城市道路網的特點，有以下分析假設：(1)所有的邊是雙向可通的，邊的權值為正值；(2)城市道路網中兩節點間有弧度的邊抽象為等距離直線的邊。進一步的，所述步驟104中，根據配送商品價格信息、配送目的地、需要商品數量、商品廠家存貨數量以及車輛需求情況給出商品供需方案，根據當前所處地理位置，在本區域內，搜索符合需求商品數量的廠家，給出一個或多個組合選擇。進一步的，所述步驟105中，由步驟104中給出的多個選擇，根據Dijkstra算法規劃各個選擇的最短路徑，若某一選擇中有多個節點，則利用Dijkstra算法規劃各個節點間的最短路徑。進一步的，所述步驟105中，所述Dijkstra算法原理為：引入一個輔助向量D，它的每個分量D[i]表示當前所找到的從起始點vs到每個節點vi的最短路徑長度；輔助向量D的初始狀態為：若從起始點vs到節點vi有邊，則每個分量D[i]為邊上的權值，否則令D[i]為無窮大∞；設集合M為求得最短路徑終點的集合，初始狀態為空集；利用Dijkstra算法對車輛到商品廠家的路徑進行規劃包括下述步驟：(1)從起始點vs出發，到各節點vi的最短路徑長度為D[i]的初值為：D[i]＝c＜vs,vi＞；(2)選擇節點vj，使得vj表示當前求得的從起始點vs出發的最短路徑終點，并且將最短路徑終點vj加入到集合M中；(3)更新從起始點vs出發到集合V-M上任一節點vk的可達最短路徑長度，如果D[k]＞D[j]+c＜vj,vk＞，則更新D[k]為D[k]＝D[j]+c＜vj,vk＞；(4)重復操作步驟(2)、(3)共n-1次，則得到從起始點vs出發到任一節點的最短路徑長度；(5)由下述公式計算得到從起始點vs到節點vd的最短路徑長度C(Psd)：C(Psd)=Σi=1n-1c(vi,vi+1)---(5-1);]]>其中：C(Psd)為從起始點vs到節點vd的最短路徑長度；n表示n個節點；c(vi,vi+1)是邊(vi,vi+1)的非負權值。進一步的，所述步驟106中，假設不同廠家的商品發往不同的目的地A，B，C，廠家Fi存有商品wi噸，價格為pi；車輛需求的商品數量為W噸，需要到m個廠家能滿足所需求的商品數量；則約束條件如下：Min(Σi=1mC(Pi-1,i))Σi=1mwi≥WMin(m)Min(pi)---(5-2);]]>其中：表示車輛經過m個廠家滿足運輸需求的最短路徑長度；wi表示廠家Fi存有的商品，單位為噸；C(Pi-1,i)表示節點i-1到節點i間的最短路徑，即為單個廠家滿足運輸需求的最短路徑長度；W表示車輛需求的商品數量，單位為噸；Pi-1,i表示節點i-1到節點i間的一條路徑；將整個城市道路網模型分為9個區域，根據車輛所處城市的不同位置，來實現由近及遠的搜索。進一步的，判斷是否滿意步驟105中給出的路徑規劃，若滿意，則Dijkstra算法結束；反之，擴大搜索區域，在所有相鄰區域(一般來說，不同城市相鄰區域值不同，以山東濟南市為例，主城區面積328km2,約合18*18km2,可知相鄰區域半徑6km。一般可認為大型城市相鄰區域半徑10km,中型城市相鄰區域半徑為5km,小型城市相鄰區域半徑為3km)內重復步驟103-步驟105，直到所有區域搜索完畢。為了對披露的實施例的一些方面有一個基本的理解，下面給出了簡單的概括。該概括部分不是泛泛評述，也不是要確定關鍵/重要組成元素或描繪這些實施例的保護范圍。其唯一目的是用簡單的形式呈現一些概念，以此作為后面的詳細說明的序言。與最接近的現有技術相比，本發明提供的技術方案具有的優異效果是：本發明提供的技術方案立足于商品配送路徑規劃，對多目標約束情況下的路徑規劃進行研究，研究商品配送路徑的規劃方法。研究在城市道路網模型的場景下，在某一地區存在多個同一商品的廠家，因商品價格的不同、不同廠家商品銷往地區不同，且廠家存有商品數量也不同，運輸商品的車輛如何根據需求來選擇商品廠家，滿足商品供需的條件，并使得車輛經過的路徑最短的問題。通過規劃最優路徑，達到節約運輸成本、提高車輛裝載率以及提高配送的效率的目的。通過研究發現，該問題其實是在多個目標條件的約束下，尋求滿足各條件下的最短路徑規劃。為此，本發明首先根據實際城市道路情況，以道路的交叉點或端點作為節點，建立了城市道路網的模型；其次確定商品價格信息，篩選符合商品發往目的地的廠家；然后根據需要商品數量以及廠家存貨數量選擇廠家，可以存在多個廠家組合以滿足需求商品數量的供需方案；最后由上一步確定的廠家地理位置和車輛位置，利用Dijkstra算法規劃最優的路徑，并采用逐級搜索的方法，提高本發明算法搜索的效率。實際運用效果表明，該方法可以根據車輛對不同商品數量的需求，很快的給出商品配送最優路徑規劃方案，在有多種供需方案下還可以給出不同的路徑規劃方案。為了上述以及相關的目的，一個或多個實施例包括后面將詳細說明并在權利要求中特別指出的特征。下面的說明以及附圖詳細說明某些示例性方面，并且其指示的僅僅是各個實施例的原則可以利用的各種方式中的一些方式。其它的益處和新穎性特征將隨著下面的詳細說明結合附圖考慮而變得明顯，所公開的實施例是要包括所有這些方面以及它們的等同。附圖說圖1是本發明提供的城市道路網示意圖；圖2是本發明提供的劃分區域的城市道路網示意圖；圖3是本發明提供的具體實施例一的基于MoCD算法的商品配送路徑規劃方法的流程圖；圖4是本發明提供的具體實施方式二的時間復雜度對比圖；圖5是本發明提供的具體實施方式二的空間復雜度對比圖；圖6是本發明提供的具體實施方式二的需求量為15噸時最優路徑示意圖；圖7是本發明提供的具體實施方式二的需求量為40噸時最優路徑示意圖。具體實施方式下面結合附圖對本發明的具體實施方式作進一步的詳細說明。以下描述和附圖充分地示出本發明的具體實施方案，以使本領域的技術人員能夠實踐它們。其他實施方案可以包括結構的、邏輯的、電氣的、過程的以及其他的改變。實施例僅代表可能的變化。除非明確要求，否則單獨的組件和功能是可選的，并且操作的順序可以變化。一些實施方案的部分和特征可以被包括在或替換其他實施方案的部分和特征。本發明的實施方案的范圍包括權利要求書的整個范圍，以及權利要求書的所有可獲得的等同物。在本文中，本發明的這些實施方案可以被單獨地或總地用術語“發明”來表示，這僅僅是為了方便，并且如果事實上公開了超過一個的發明，不是要自動地限制該應用的范圍為任何單個發明或發明構思。本發明首先根據實際城市道路情況，以道路的交叉點或端點作為節點，建立了城市道路網的模型；其次確定商品價格信息，篩選符合商品發往目的地的廠家；然后根據需要商品數量以及廠家存貨數量選擇廠家，可以存在多個廠家組合以滿足需求商品數量的供需方案；最后由上一步確定的廠家地理位置和車輛位置，利用Dijkstra算法規劃最優的路徑，，并采用逐級搜索的方法，提高本發明算法搜索的效率。實施例一本發明提供一種基于MoCD算法的商品配送路徑規劃方法，包括下述步驟：步驟101：建立城市道路網模型；步驟102：確定商品價格信息；步驟103：根據不同廠家商品的配送目的地，篩選符合要求目的地的廠家；步驟104：確定商品供需方案；步驟105：利用Dijkstra算法對車輛到商品廠家的路徑進行規劃；步驟106：采用逐級搜索方式對城市道路網模型劃分區域進行搜索；步驟107：輸出最優路徑規劃方案，結束。具體的：步驟101中，本發明建立了城市道路網的模型：縱橫交織、錯綜復雜的城市道路網主要由眾多街道相交、相連而構成，一條街道可能與若干條街道相交、相連，并且相交、相連的模式復雜。為了避免過多地考慮街道間的拓撲關系，以交叉路口作為分析對象，將包含交叉路口的道路拆分成最基本的路段，一條路段只在其端點處與其他路段相交。在數字地圖中，定義一條道路的交叉點或端點作為道路網的節點,節點有相對的經度、緯度地理坐標，兩節點間的路段定義為網絡的邊，路段的距離定義為邊的權值。根據城市道路網的特點,有以下合理的分析假設：(1)所有的邊是雙向可通的，邊的權值為正值；(2)網絡中兩節點間有弧度的邊抽象為等距離直線的邊。由以上假設，我們可以把城市道路網抽象為如圖1所示。圖1中五角星表示待配送商品的廠家位置，節點間的權值為它們之間的實際距離，單位為km。在圖1中，在進行從某一地點到某一廠家的最短路徑計算時，本發明將廠家地點與其最近的節點視為同一節點，然后再根據相應來車方向相應的增加或減少廠家與最近節點的距離，以此來實現最短路徑的計算，達到減少圖中節點數目，減少最優路徑的搜索時間。步驟104中，根據配送商品價格信息、配送目的地、需要商品數量、商品廠家存貨數量以及車輛需求情況給出商品供需方案，根據當前所處地理位置，在本區域內，搜索符合需求商品數量的廠家，給出一個或多個組合選擇。步驟105中，由步驟104中給出的多個選擇，根據Dijkstra算法規劃各個選擇的最短路徑，若某一選擇中有多個節點，則利用Dijkstra算法規劃各個節點間的最短路徑。假設現在需要運輸一批商品，此時車輛在圖1中A點，需要去某廠家運輸商品，這時就需搜尋合適的廠家，以達到路徑最短，且盡量滿足運輸量。在搜索路徑的時候，根據Dijkstra算法來實現距離最短的路徑，下面先介紹下Dijkstra算法。在圖論中，給定帶權圖G＝(V，E)，其中V是包含n個節點的集合，E是包含m條邊的集合，＜v,w＞是E中從v到w的邊，c＜v,w＞是邊＜v,w＞的非負權值，設a,b是V中的節點，Pab＝{v0＝a,v1,…,vn＝b}是V中由a到b的一條路徑，則路徑Pab的權值總和C(Pab)表示為：C(Pab)=Σi=1n-1c(vi,vi+1)]]>因此最短路徑問題就是在帶權的圖中，尋找從指定起點到終點的一條權值總和最小的路徑。Dijkstra算法的原理如下：(1)引入一個輔助向量D，它的每個分量D[i]表示當前所找到的從起始點vs到每個中間點vi的最短路徑長度。D的初始狀態為：若從vs到vi有邊，則D[i]為邊上的權值，否則令D[i]為∞。設集合M為求得最短路徑終點的集合，初始狀態為空集。最短路徑生成過程如下：(2)從vs出發，到圖上其他各節點vi的可能最短路徑長度為D[i]的初值為：D[i]＝c＜vs,vi＞；(3)選擇vj，使得vj就是當前求得的從vs出發的最短路徑終點，并且將vj加入到集合M中。(4)更新從vs出發到集合V-M上任一節點vk的可達最短路徑長度，如果D[k]＞D[j]+c＜vj,vk＞，則更新D[k]為D[k]＝D[j]+c＜vj,vk＞；(5)重復操作(2)、(3)共n-1次，則可得到從vs出發到任一節點的最短路徑長度。(6)最后由下述公式(5-1)計算得到從vs到vd的最短路徑長度C(Psd)：C(Psd)=Σi=1n-1c(vi,vi+1)---(5-1);]]>其中：C(Psd)為從起始點vs到節點vd的最短路徑長度；n表示n個節點；c(vi,vi+1)是邊(vi,vi+1)的非負權值。步驟106中，由Dijkstra算法可以得到從某一節點到其它節點的最短路徑長度，但運輸車輛在選擇某廠家運輸商品時還要考慮到商品發往的目的地、數量、價格等因素，加入其它條件肯定會導致算法搜索時間增多，因此本發明根據以上算法思想，提出了本發明的算法，基于Dijkstra算法的多目標約束(MoCD，Multi-objectiveConstraintDijkstra)的商品配送路徑規劃算法，簡稱MoCD算法。假設不同廠家的商品發往不同的目的地A，B，C，廠家Fi存有商品wi噸，價格為pi。車輛需求的商品數量為W噸，需要到m個廠家能滿足所需求的商品數量。則我們的約束條件如下：Min(Σi=1mC(Pi-1,i))Σi=1mwi≥WMin(m)Min(pi),---(5-2)]]>其中：表示車輛經過m個廠家滿足運輸需求的最短路徑長度；wi表示廠家Fi存有的商品，單位為噸；C(Pi-1,i)表示節點i-1到節點i間的最短路徑，即為單個廠家滿足運輸需求的最短路徑長度；W表示車輛需求的商品數量，單位為噸；Pi-1,i表示節點i-1到節點i間的一條路徑；然而在多目標的約束條件下，算法的搜索時間肯定會增大，因此我們引入逐級搜索的方法。如圖2中，將整個城市道路網分為9個區域，根據車輛所處城市的不同位置，來實現由近及遠的搜索。本發明算法的流程圖如圖3所示。實施例二本發明根據山東省某市區內的66家鋼材廠家對所提算法進行驗證，將基于Dijkstra算法的商品配送路徑規劃算法應用到某公司開發的App當中，根據手機App中的裝貨推薦功能對本發明算法的實用性進行驗證。下面主要從不同算法搜索路徑的時間和規劃方案來進行說明。(1)計算時間是衡量算法性能的因素之一。考慮66個鋼材廠家，某車輛需要運輸發往北京的某種鋼材，我們根據手機App給出搜索出的最優路徑時間作為算法的計算時間，運行10次求其均值，以下給出蟻群算法和本發明算法的平均計算時間。表1三種算法的平均計算時間從表1可以看出，本發明的算法與蟻群算法相比，路徑搜索時間較短，在實際應用中用戶體驗較好。(2)算法復雜度。算法的復雜度包括時間復雜度和空間復雜度，時間復雜度主要是算法搜索最優路徑所需的時間與節點數量的關系；空間復雜度主要是算法在運行時占用的內存資源。蟻群算法的時間復雜度為O(n4)，空間復雜度為O(n2)；Dijkstra算法的時間復雜度為O(n2)，空間復雜度為O(n)；本發明的算法是基于Dijkstra算法，其中給出商品數量供需方案時的時間復雜度為O(n)，空間復雜度為O(1)。因此，本發明中的MoCD算法的時間復雜度為T(n)＝O(n2)+O(n)＝O(n2)；空間復雜度S(n)＝O(n)+O(1)＝O(n)。如圖4、5所示，由圖4、圖5可以看出，蟻群算法在計算時會耗費大量的時間和內存資源，而本發明的MoCD算法的計算時間和計算開銷則大大降低，采用逐級搜索的方式可以進一步降低算法的搜索時間和對內存資源的占用。(3)規劃方案。考慮某市區內的66家鋼材廠家，某車輛在不同的初始位置，需求發往北京的某種鋼材分別為15噸和40噸時，本發明給出的最優路徑規劃方案如下。某車輛在需求量為15噸時，此地區內廠家滿足其需求，并且路徑最短的規劃方案結果如圖6所示。某車輛某時刻在另一地點，需求量為40噸時，給出了兩個廠家組合滿足其需求的方案，此時路徑規劃方案的結果如圖7所示。本發明提供的方法結合城市中道路實際情況，以道路交叉點或端點為節點，建立了城市道路網模型，并將廠家位置與其最近節點視為同一節點，減少了模型中節點的數量；針對多個目標約束下的商品配送路徑規劃問題，建立了以滿足車輛需求商品數量為目標，由車輛位置和滿足需求的廠家位置運用Dijkstra算法進行路徑規劃。并將城市進行分區，采用逐級搜索的方法進行路徑的規劃，提高了最優路徑的搜索效率。應該明白，公開的過程中的步驟的特定順序或層次是示例性方法的實例。基于設計偏好，應該理解，過程中的步驟的特定順序或層次可以在不脫離本公開的保護范圍的情況下得到重新安排。所附的方法權利要求以示例性的順序給出了各種步驟的要素，并且不是要限于所述的特定順序或層次。在上述的詳細描述中，各種特征一起組合在單個的實施方案中，以簡化本公開。不應該將這種公開方法解釋為反映了這樣的意圖，即，所要求保護的主題的實施方案需要清楚地在每個權利要求中所陳述的特征更多的特征。相反，如所附的權利要求書所反映的那樣，本發明處于比所公開的單個實施方案的全部特征少的狀態。因此，所附的權利要求書特此清楚地被并入詳細描述中，其中每項權利要求獨自作為本發明單獨的優選實施方案。最后應當說明的是：以上實施例僅用以說明本發明的技術方案而非對其限制，盡管參照上述實施例對本發明進行了詳細的說明，所屬領域的普通技術人員依然可以對本發明的具體實施方式進行修改或者等同替換，這些未脫離本發明精神和范圍的任何修改或者等同替換，均在申請待批的本發明的權利要求保護范圍之內。當前第1頁1 2 3