一種基于自適應時間步長的瞬變電磁?溫度場耦合計算方法與流程
本發明一種基于自適應時間步長的瞬變電磁-溫度場耦合計算方法,涉及電磁溫度計算領域。
背景技術:
在線圈發射裝置、繼電器、電機等設備中,運行時產生過高的溫升將影響線圈和接頭導電性、材料的絕緣性能,甚至會產生破壞性的熱膨脹,對于設備運行性能及安全性產生一定的影響。在上述問題中,瞬變的大電流使得導體的溫度在較短的時間內迅速增加,因而在計算過程不僅考慮電磁場對溫度場的影響,還需考慮溫度變化對電磁場材料導電性能的影響,為此需要建立瞬變電磁-溫度場順序強耦合模型。目前采用有限元法求解瞬變電磁-溫度場間接耦合時,電磁場和溫度場往往采用相同的時間步長。然而在求解過程中,溫度場響應較電磁場慢,若采用相同的時間步長計算,使得溫度場求解過頻,造成了求解時間的增加。
對于兩物理場瞬態間接耦合時,物理場響應時間不同的問題。有方法根據現有軟件,提出代碼耦合概念,對各物理場采用不同的時間離散策略,并在時間的耦合點上進行載荷的傳遞。也有方法針對在流-固耦合時,對流體區域和固體區域采用不同的時間步長的DFMT-SCSS算法,選取固體求解區域時間步長為流體求解區域的倍數計算。然而上述方法在計算兩物理場耦合時,兩物理場時間步長只是存在簡單的倍數關系,而物理場都采用恒定步長計算,存在兩物理場未獲得最佳離散策略的情況。為此提出自適應步長耦合概念,即各物理場采用自適應步長算法獲取最佳離散時間策略,并在預測的耦合時間節點上自動耦合。可以使各物理場獲得最佳的時間離散策略,也避免了響應較慢的物理場過頻的計算。
技術實現要素:
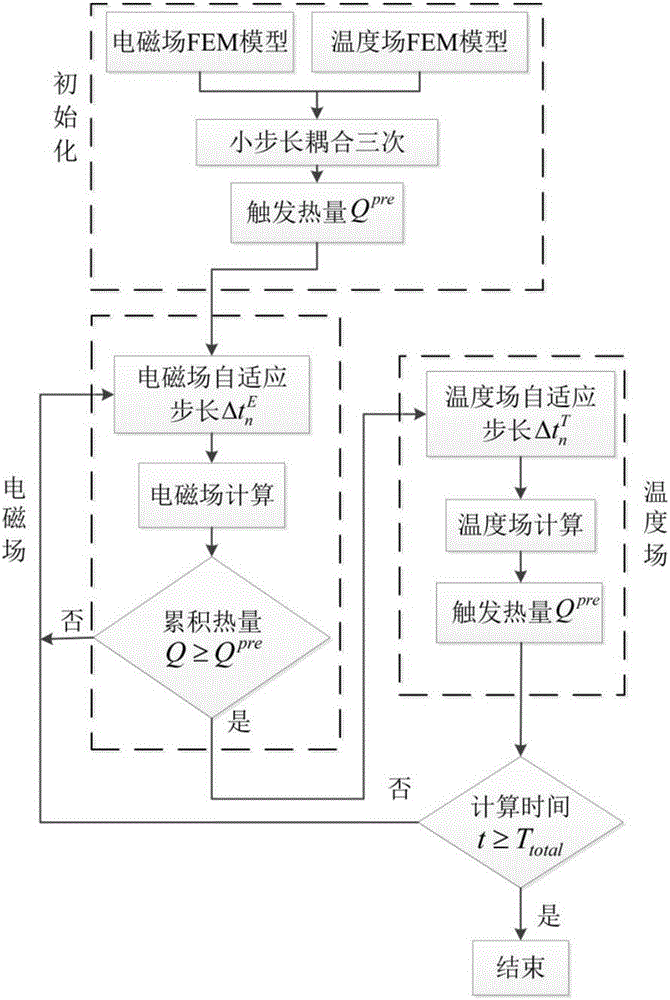
為解決上述技術問題,針對瞬態電磁-溫度場間接耦合問題,本發明提出一種基于自適應時間步長的瞬變電磁-溫度場耦合計算方法。在Tn時刻,如圖1所示,首先通過指數平滑法預測下一耦合時間點Tn+1。然后在兩耦合時間節點間,通過預測-校正法和響應特征值計算電磁場和溫度場最佳離散步長。得到Tn至Tn+1時間段內電磁場和溫度場最佳時間離散步長為△tnE和△tnT。電磁場、溫度場分別采用△tnE、△tnT計算至耦合時間節點。使各物理場在兩耦合時間節點上,以最佳的時間步長計算,避免了響應較慢的物理場過頻的計算。
本發明所采用的技術方案是:
一種基于自適應時間步長的瞬變電磁-溫度場耦合計算方法,包括以下步驟:
1)、初始化。首先建立分析對象的電磁場和溫度計算有限元模型,并給定電磁場計算中的磁導率、電阻率和溫度場計算的比熱容、導熱率等材料參數。最后施加初始條件、邊界及載荷;
2)、耦合時間點確定。采用溫度場觸發熱量來判斷電磁溫度場耦合時間節點。首先電磁-溫度場采用較小步長耦合三次,用來獲取溫度場觸發熱量Qpre的預測數據。然后采用指數平滑法預測溫度場觸發熱量,通過觸發熱量判斷耦合時間節點;
3)、電磁場自適應步長計算。通過載荷離散誤差和響應特征值確定電磁場載荷最佳離散的步長△tnE。啟動電磁場,采用最佳離散步長計算。當電磁場累積熱量達到溫度場觸發熱量時,暫停電磁場計算;
4)、溫度場自適應步長計算。同3)中,通過載荷離散誤差和響應特征值確定電磁場載荷最佳離散的步長△tnT。將電磁場計算平均熱功率作為載荷加至溫度場,當溫度場計算時間與電磁場同步時,暫停溫度場計算。更新電磁場節點溫度,并進行下一時間步的溫度場觸發熱量計算。反復迭代計算至最終時間。
本發明一種基于自適應時間步長的瞬變電磁-溫度場耦合計算方法,優點在于:
1)、由于順序耦合時,在計算電磁場的單個時間步內,并未考慮溫度場的變化,因而存在累積的非平衡誤差。采用溫度場觸發熱量來判斷耦合時間節點,可以有效控制非平衡誤差。
2)、與傳統等步長耦合方法相比,避免了由于溫度場響應時間比電磁場長,而采用統一計算時間步長導致溫度場求解次數過多而增加計算時間的問題,減小了計算時間。
附圖說明
圖1是電磁-溫度場自適應耦合示意圖。
圖2是電磁-溫度場自適應步長耦合流程圖。
圖3是載荷離散誤差圖。
圖4(a)是銅導環結構示意圖;
圖4(b)是有限元模型圖。
圖5(a)等步長溫度計算溫度分布圖;
圖5(b)自適應步長溫度分布圖。
圖6(a)是1號單元計算結果圖;
圖6(b)是140號單元計算結果圖。
具體實施方式
一種基于自適應時間步長的瞬變電磁-溫度場耦合計算方法,包括以下步驟:
1)、初始化。首先建立分析對象的電磁場和溫度計算有限元模型,并給定電磁場計算中的磁導率、電阻率和溫度場計算的比熱容、導熱率等材料參數。最后施加相應的初始條件、邊界及載荷;
2)、耦合時間點確定。采用溫度場觸發熱量來判斷電磁溫度場耦合時間節點。首先電磁-溫度場采用較小步長耦合三次,用來獲取溫度場觸發熱量Qpre的預測數據。然后采用指數平滑法預測溫度場觸發熱量,通過觸發熱量判斷耦合時間節點;
3)、電磁場自適應步長計算。通過載荷離散誤差和響應特征值確定電磁場載荷最佳離散的步長△tnE。啟動電磁場,采用最佳離散步長計算。當電磁場累積熱量達到溫度場觸發熱量時,暫停電磁場計算;
4)、溫度場自適應步長計算。同3)中,通過載荷離散誤差和響應特征值確定電磁場載荷最佳離散的步長△tnT。將電磁場計算平均熱功率作為載荷加至溫度場,當溫度場計算時間與電磁場同步時,暫停溫度場計算。更新電磁場節點溫度,并進行下一時間步的溫度場觸發熱量計算。反復迭代計算至最終時間。
具體步驟如下:
步驟1):建立電磁場計算有限元模型,并給定磁導率、電阻率材料參數,施加載荷。由似穩條件忽略位移電流,時變電磁場方程可寫為如下形式的矢量磁位方程:
式中:Ω1為導體區域,Ω2為非導體區域。A為矢量磁位(Wb/m);V為電位(V);σ為電導率(S/m);μ為磁導率(H/m);Js為源電流密度(A/m2)。
采用伽遼金法將上式寫成有限元格式:
式中:R為電磁場阻尼矩陣;S為電磁場系數矩陣;J為磁場載荷矩陣。
步驟2):建立溫度場場計算有限元模型,并給定比熱容、導熱率材料參數。在只考慮熱傳導和對流條件下,溫度場導熱微分方程可寫成如下形式:
式中:ρ為密度(Kg/m),Cp為比熱容(J/(Kg.K)),Q為發熱功率W。
初始條件及邊界條件為:
式中:G(x,y,z)表示初始溫度分布;F(x,y,z)表示恒定溫度邊界條件;Γq表示散熱量邊界條件,q為邊界發熱功率,h為邊界對流換熱系數。
采用伽遼金法將式(3),(4)形成有限元格式如下:
式中:C為溫度場比熱矩陣,K為溫度場導熱矩陣,P為載荷矩陣。
步驟3):采用溫度場觸發熱量來判斷電磁溫度場耦合時間節點。電磁-溫度場采用較小步長耦合三次,用來獲取溫度場觸發熱量Qpre的預測數據。
步驟4):獲取電磁場計算過程中允許材料變化最大溫度。線性材料熱功率P與電流密度為J關系:
Pn=∫VJn2ε(T)dV (6)
ε=aT+ε0 (7)
式中:V為單元體積,Pn為tn時刻發熱功率。Jn為Tn時刻電流密度,ε為電阻率,a為電阻隨溫度變化率,ε0為0℃時電阻率。
當輸入熱功率為Pn,由溫度變化引起功率計算誤差應滿足:
|Pn(Tn)-Pn(Tn+△T)|≤γPn(Tn) (8)
式(8)取等號時,可得出Tn時刻溫度允許變化最大值△Tmax。
步驟5):溫度場觸發熱量計算。根據Tn時刻最大溫度變化△Tmax。由Tn,Tn-1,Tn-2時刻輸入功率及溫度變化,預測Tn+1溫度場觸發熱量
首先計算各時刻輸入熱量及溫度變化,如表1。
表1各時刻熱量、溫度
再計算各時刻溫度隨熱量變化率,如表2。
表2時刻溫度變化率
最后計算溫度場觸發熱量計算。采用指數平滑方法預測tn+1時刻溫度場變化率Kn+1:
Kn+1=αKn+(1-α)Kn-1+(1-α)2Kn-2 (9)
溫度場觸發熱量為:
Qpre=△TmaxKn+1 (10)
步驟6):啟動電磁場,根據載荷離散誤差確定電磁場時間步長t∈(tn-1,tn)時,當載荷矩陣P采用線性插值時,等效載荷采用斜坡加載,如圖3所示。由載荷離散產生的誤差為如式(13)。
對式(13)采用梯形公式積分,得離散誤差近似如式(14)。
根據式(14),載荷離散誤差近似正比于(△t)2,可將下一步長計算可分為如下兩步:
(a)步長預測。根據第n步計算誤差,預測第n+1步長△t1n+1。
式中:為安全系數,etolerance為允許最大誤差;為第n時間步內產生的離散誤差。
(b)步長校正。判斷當第n+1時間步長△t1n+1所產生誤差是否滿足ek+1<etolerance。如不滿足采用(8)進行修正迭代計算,直至滿足ek<etolerance。
式中:為安全系數,
步驟7):根據響應特征值確定電磁場時間步長Hughes提出根據響應特征λr值確定計算穩定時間步長△tn+1的方法[16],定義△tn+1λ為震蕩限制條件。當△tn+1λ>>1時系統處于震蕩狀態。為保證計算穩定性可取最大步長需滿足:
式中:f<1,f為穩定系數;λr為響應特征值;△un為tn-1到tn時間段場量u的變化。
步驟8):電磁場在tn時刻離散時間步長為:
步驟9):耦合時間判斷。當Tn+1時刻電磁場累積熱量滿足以下條件之一時,Tn+1為電磁-溫度場耦合時間點,啟動溫度場計算。
(a)單元最大熱量變化達到步驟5)中單元預測熱量閾值時自動啟動溫度場計算:
(b)總體熱量變化達到步驟5)中單元預測熱量閾值時自動啟動溫度場計算:
步驟10):啟動溫度場計算,計算溫度場自適應時間步長溫度場自適應時間步長計算同步驟6)、步驟7)、步驟8);
步驟11):當溫度場計算時間到達步驟9)中耦合時間Tn+1時,停止溫度場計算,更新電磁場節點溫度。
步驟12):反復迭代步驟4)~步驟10),直至計算總時間Ttotal。
實施例:
以通電銅導環瞬態溫升為例:
本節以電銅導環熱分析為例說明自適應時間步長在電磁-熱耦合中的應用,該模型廣泛存在于繼電器、線圈發射等裝置中。將一長10mm,厚2mm銅導環置于空氣中,如圖4(a)所示),銅導環的上下及內外表面對流換熱系數均為5W/m2。對銅導環施加電流i=104sin(50πt),持續時間0.1s,分析銅環的溫度變化。
建立軸對稱模型,如圖5(b)所示,電磁場計算區域包含銅環、空氣區域,采用三角劃分網格,共988個節點,2061個單元。溫度場計算區域為銅環區域,也采用三角形劃分網格,共121個節點,200個單元。
當式(15)中電磁場載荷離散誤差取為etolerance=0.5%,式(8)、式(21)中取γ=1%,β=1。電磁-溫度場前三個時間步內采用1ms耦合,隨后采用自適應時間步長耦合。最后將自適應時間步長計算結果與定步長計算結果對比,如圖5(a)、圖5(b)所示,分別為銅導環施加交流載荷0.1s時,采用等步長和自適應時間步長計算所得的溫度分布云圖。
由圖6(a)、圖6(b)可見,采用自適應時間步長所得的銅環溫度分布與定步長溫度分布基本一致。其中1號單元溫度最高而相對誤差最小為0.35%,140號單元溫度最低而相對誤差最大為0.53%。為此選取1號單元和140號單元,分析其在整個加熱過程中溫度及誤差的變化規律。
1號和140號在0.1s內自適應時間步長與定步長計算所得單元溫度對比如圖6(a)、圖6(b)所示,銅導塊溫度近似以0.02s為周期上升。以0.06s~0.08s為例,在區域a和c中,電流幅值較小,溫度場升較慢,對應的溫度場計算步長較大。而區域b,電流幅值較大,溫度上升較快,對應溫度場計算時間步長較小,說明電磁-溫度場自動步長耦合算法的有效性。在整個計算過程中,自動步長計算與定步長計算誤差在在0.7%以內,明了該方法的準確性。
電磁-溫度場自適應時間步長與定步長耦合計算性能對比如表3所示。在0.1s內,采用定步長耦合,選取時間步長為1ms時,電磁場和溫度場均需計算100次,整體計算時間為235s。而采用自適應步長求解時,電磁場計算93次,溫度場計算29次,計算時間為184s,計算時間減小21%。
表3計算性能對比
- 還沒有人留言評論。精彩留言會獲得點贊!