一種復雜油氣儲層滲透率的定量評價方法與流程

本發明涉及一種復雜油氣儲層滲透率的定量評價方法，屬于石油勘探領域。

背景技術：

現有的儲層滲透率計算，主要是基于孔隙度和滲透率之間高精度的函數關系，采用孔隙度去建立儲層滲透率的計算公式。而對于復雜的油氣儲層來說，由于儲層的強非均質性，致使在均質儲層中孔隙度與滲透率之間高精度的函數關系并不存在。因此基于孔隙度和滲透率之間高精度的函數關系去計算復雜油氣儲層的滲透率并不可行。而針對復雜油氣儲層滲透率的計算包括兩種方法，一種是基于核磁測井資料在自由流體模型中計算滲透率，另一種是在平均T₂模型中計算滲透率，但當復雜油氣儲層缺乏核磁測井和成像測井等特殊測井資料的情況下，也就無法基于上述兩種方法來準確獲取復雜油氣儲層的滲透率。為了準確計算復雜油氣儲層的滲透率，必須對復雜油氣儲層進行分類，然后再在每一類中，基于孔隙度與滲透率之間高精度的函數關系，采用孔隙度去計算滲透率。但常規的分類方法，要么難以準確分類，要么難以推廣應用。

其中，基于核磁測井資料在自由流體模型中計算滲透率的計算公式為：

式中：K為滲透率；為孔隙度；C為經驗常數；FFI為自由流體的孔隙體積；BVI為束縛水的孔隙體積。

基于平均T₂模型計算滲透率其計算公式為：

式中：K為滲透率，mD；a為經驗常數；T_2gm是T₂分布的幾何平均值；為孔隙度。

技術實現要素：

針對上述問題，本發明的目的是提供一種基于流動單元和分類算法耦合的能夠準確計算復雜油氣儲層滲透率的定量評價方法。

為實現上述目的，本發明采取以下技術方案：一種復雜油氣儲層滲透率的定量評價方法，其包括以下步驟：

1)基于巖心樣品的物性分析結果，計算不同深度儲層的儲層品質因子和巖石孔隙體積與顆粒體積比；

2)根據不同深度儲層的儲層品質因子和巖石孔隙體積與顆粒體積比，計算不同深度儲層的流動單元指標；

3)將計算得到的不同深度儲層的流動單元指標細分為多個分布范圍，并使得每一流動單元指標的范圍區間對應著一類復雜油氣儲層；

4)針對細分后每一流動單元指標的范圍區間所對應的復雜油氣儲層的類別，采用分類算法，建立基于不同測井曲線數值劃分每一類復雜油氣儲層類別的分類模型；

5)通過每一類復雜油氣儲層的分類模型去劃分一口井整個井段的類別，針對每個井段復雜油氣儲層所屬的類別，獲取相應的孔隙度與滲透率之間的函數關系來計算該類別中復雜油氣儲層的滲透率，利用不同類別復雜油氣儲層滲透率的組合，完成整個井段復雜油氣儲層滲透率的定量評價。

所述步驟1)中，儲層品質因子的計算公式為：

式中，RQI為儲層品質因子；K為滲透率；為孔隙度。

所述步驟1)中，巖石孔隙體積與顆粒體積比的計算公式為：

式中，為巖石孔隙體積與顆粒體積比。

所述步驟2)中，流動單元指標的計算公式為：

式中，FZI為流動單元指標；RQI為儲層品質因子；為巖石孔隙體積與顆粒體積比。

所述步驟3)中，當每個分布范圍內的孔隙度與滲透率之間的函數關系均滿足所對應的一類復雜油氣儲層的滲透率計算精度的80％時，則以該細分范圍為準；如若不滿足所對應的一類復雜油氣儲層的滲透率計算精度的80％時，則需重新對不同儲層深度的流動單元指標FZI細分，直到細分后的每個范圍的孔隙度與滲透率之間的函數關系均滿足所對應的一類復雜油氣儲層的滲透率計算精度的80％為止。

每一類復雜油氣儲層孔隙度與滲透率之間的函數關系為：

式中，K為滲透率；為孔隙度；a、b為常數。

所述步驟4)中，分類模型可通過Geolog、GeoFrame、Forward或Lead軟件進行建立。

本發明由于采取以上技術方案，其具有以下優點：1、本發明方法避免開展大量的巖心實驗，能夠有效地節約成本，具有較強的經濟性。2、本發明方法基于流動單元和分類算法耦合來準確計算復雜油氣儲層的滲透率，在保證復雜油氣儲層滲透率定量評價結果準確性的同時，提供了一種簡單實用的新方法。

附圖說明

圖1是A井白云巖儲層分類前孔隙度與滲透率的交會圖；

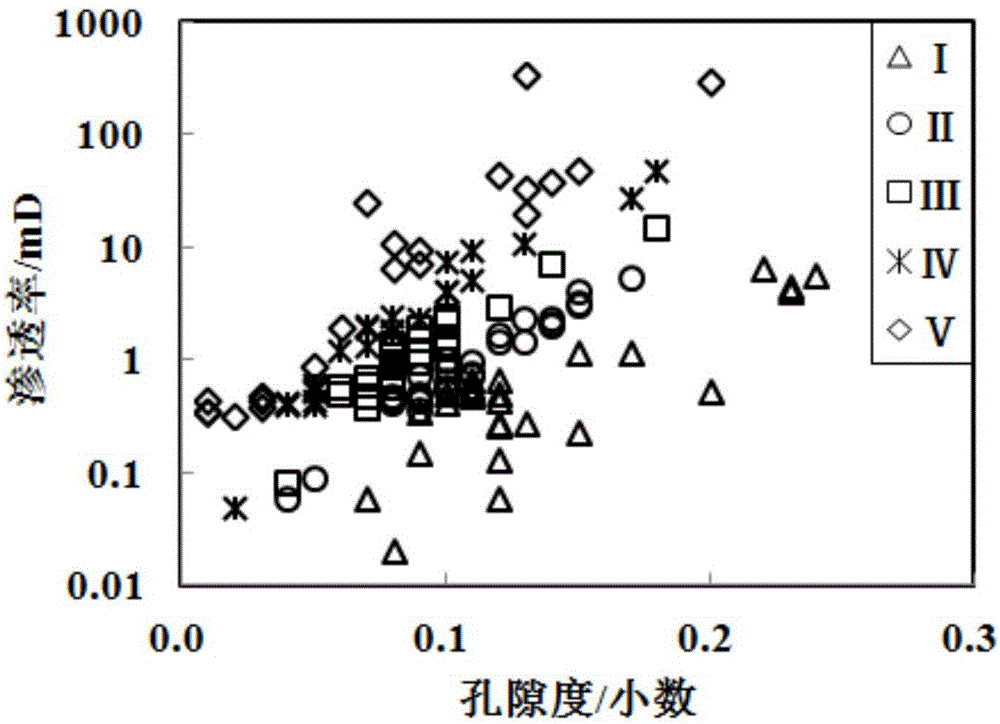
圖2是A井白云巖儲層分類后孔隙度與滲透率的交會圖；

圖3是A井白云巖儲層分類模型中不同測井曲線敏感性分析結果；

圖4是A井白云巖儲層基于流動單元和分類算法耦合的滲透率評價結果；

圖5是B井石灰巖儲層分類前孔隙度與滲透率的交會圖；

圖6是B井石灰巖儲層分類后孔隙度與滲透率的交會圖；

圖7是B井石灰巖儲層分類模型中不同測井曲線敏感性分析結果；

圖8是B井石灰巖儲層基于流動單元和分類算法耦合的滲透率評價結果。

具體實施方式

下面結合附圖和實施例對本發明進行詳細的描述。

本發明涉及一種復雜油氣儲層滲透率的定量評價方法，其包括以下步驟：

1)基于巖心樣品的物性分析結果，計算不同深度儲層的儲層品質因子RQI，計算公式為：

式中，RQI為儲層品質因子；K為滲透率；為孔隙度。

2)基于巖心樣品的物性分析結果，計算不同深度儲層的巖石孔隙體積與顆粒體積比計算公式為：

3)根據上述步驟1)和步驟2)中，儲層品質因子RQI和巖石孔隙體積與顆粒體積比計算不同深度儲層的流動單元指標FZI，計算公式為：

4)將計算得到的不同深度儲層的流動單元指標FZI細分為多個分布范圍，并使得每一流動單元指標FZI的范圍區間對應著一類復雜油氣儲層，分類方式如下：

Ι＝f(a＜FZI≤b),ΙΙ＝f(c＜FZI≤d),ΙΙΙ＝f(e＜FZI≤f)…

式中，Ι、ΙΙ、ΙΙΙ為復雜油氣儲層所屬的類別號；FZI為流動單元指標；a、b、c、d、e、f為流動單元指標數值。

當每個分布范圍內的孔隙度與滲透率之間的函數關系均滿足所對應的一類復雜油氣儲層滲透率計算的精度時，則以該細分范圍為準；如若不滿足所對應的一類復雜油氣儲層滲透率計算的精度時，則需重新對不同深度儲層的流動單元指標FZI細分，直到細分后每個范圍的孔隙度與滲透率之間的函數關系均滿足所對應的一類復雜油氣儲層滲透率計算的精度為止。其中，每一類復雜油氣儲層孔隙度與滲透率之間的函數關系如下：

式中，K為滲透率；為孔隙度；a、b為常數。

5)針對細分后每一流動單元指標FZI的范圍區間所對應的復雜油氣儲層的類別，采用分類算法，建立基于不同測井曲線數值劃分不同復雜油氣儲層類別的分類模型。

通過反復調整復雜油氣儲層的類別和不同測井曲線數值的組合，在保證每一類復雜油氣儲層孔隙度與滲透率之間的函數關系滿足滲透率計算精度的同時，最大程度地提高分類模型的精度。

6)基于不同測井曲線數值的組合，采用復雜油氣儲層的分類模型去劃分一口井整個井段的類別。針對每個井段復雜油氣儲層所屬的類別，采用相應的孔隙度與滲透率之間的函數關系來計算該類別中復雜油氣儲層的滲透率。利用不同類別復雜油氣儲層滲透率的組合，便完成了整個井段復雜油氣儲層滲透率的定量評價。其中，每一類復雜油氣儲層孔隙度與滲透率之間的函數關系如下：

式中，K為滲透率；為孔隙度；a、b為常數。

上述步驟4)中，大多數情況下，當每個分布范圍內的孔隙度與滲透率之間的函數關系能夠達到所對應的一類復雜油氣儲層滲透率精度的80％，即滿足要求。

上述步驟5)中，分類模型可通過Geolog、GeoFrame、Forward、Lead等軟件進行建立。

下面通過具體實施例對本發明方法做進一步說明。

實施例1：以某油田A井的白云巖儲層為例。

1)基于A井白云巖儲層巖心分析的孔隙度和滲透率，分別計算不同深度儲層的儲層品質因子RQI、巖石孔隙體積與顆粒體積比和流動單元指標FZI。

2)對不同深度儲層流動單元指標FZI的分布范圍進行細分，細分之后使得每一流動單元指標FZI的范圍區間對應著一類白云巖儲層，并為白云巖儲層所屬的類別進行編號，如Ⅰ、Ⅱ、Ⅲ……，分別建立每一類白云巖儲層孔隙度與滲透率之間的函數關系并滿足每一類白云巖儲層滲透率計算的精度要求。分類前，A井白云巖儲層孔隙度與滲透率的交會圖如圖1所示，分類后，A井白云巖儲層孔隙度與滲透率的交會圖如圖2所示。流動單元指標FZI劃分方案及相應的孔隙度與滲透率之間函數關系精度見表1。

表1流動單元指標FZI劃分方案及孔隙度與滲透率之間函數關系精度

3)基于不同測井曲線數值，采用決策樹分類算法針對表1中三種分類方案所對應的白云巖儲層類型，分別建立分類模型，其測井曲線敏感性分析結果如圖3所示，分類模型的精度見表2。

表2流動單元指標FZI分類模型的精度

4)基于表1中孔隙度與滲透率之間函數關系精度，和表2中流動單元指標FZI分類模型的精度，可以看出方案二、三流動單元指標FZI分類模型的精度大于方案一，而方案三孔隙度與滲透率之間函數關系精度高于方案二，因此，方案三為最佳方案。分類方案三所對應的孔隙度與滲透率之間函數關系與分類模型的精度見表3。

表3分類方案三所對應的孔隙度與滲透率之間函數關系與分類模型的精度

5)采用分類方案三所對應的分類模型，對A井白云巖儲層全井段進行儲層類型的劃分，將其分為五類，劃分結果如圖4中的第9道。基于表3中每一類白云巖儲層孔隙度與滲透率之間函數關系，可以計算得到每一類白云巖儲層的滲透率。將所計算五類白云巖儲層的滲透率進行組合，便能得到A井白云巖儲層全井段的滲透率，從而達到定量評價A井白云巖儲層滲透率的目的。

如圖4所示，在A井白云巖儲層基于流動單元和分類算法耦合的滲透率評價成果圖中，第1道是自然伽馬、自然電位和井徑測井曲線，表示該地層的巖性及井況特征；第2道是體積密度、中子孔隙度和縱波時差測井曲線，反映該地層的物性特征；第3道是深、中、淺電阻率測井曲線，刻畫該地層的電性特征；第5道是基于上述測井曲線所計算的孔隙度與巖心分析的孔隙度；第6道是分類前，基于孔隙度所計算的滲透率與巖心分析的滲透率，二者誤差相對較大，平均絕對誤差為15.13mD；第7道是分類后，基于流動單元和分類算法耦合所計算的滲透率與巖心分析的滲透率，二者誤差相對較小，平均絕對誤差為7.44mD。

實施例2：以某油田B井的石灰巖儲層為例。

1)基于B井石灰巖儲層巖心分析的孔隙度和滲透率，分別計算不同深度儲層的儲層品質因子RQI、巖石孔隙體積與顆粒體積比和流動單元指標FZI。

2)對不同深度儲層的流動單元指標FZI的分布范圍進行細分，細分之后使得每一流動單元指標FZI的范圍區間對應著一類石灰巖儲層并為石灰巖儲層所屬的類別進行編號，如Ⅰ、Ⅱ、Ⅲ……，分別建立每一類石灰巖儲層孔隙度與滲透率之間的函數關系。分類前，B井石灰巖儲層孔隙度與滲透率的交會圖見圖5；分類后，B井石灰巖儲層孔隙度與滲透率的交會圖如圖6所示。流動單元指標FZI劃分方案，及相應的孔隙度與滲透率之間函數關系精度見表4。

表4流動單元指標FZI劃分方案及孔隙度與滲透率之間函數關系精度

3)基于不同測井曲線數值，采用決策樹分類算法針對表4中三種分類方案所對應的石灰巖儲層類型，分別建立分類模型，其測井曲線敏感性分析結果如圖7所示，分類模型的精度見表5。

表5流動單元指標FZI分類模型的精度

4)基于表4中孔隙度與滲透率之間函數關系精度，和表5中流動單元指標FZI分類模型的精度，分類方案三為最佳方案。分類方案三所對應的孔隙度與滲透率之間函數關系與分類模型的精度見表3。

表6分類方案三所對應的孔隙度與滲透率之間函數關系與分類模型的精度

5)采用分類方案三所對應的分類模型，對B井石灰巖儲層全井段進行儲層類型的劃分，將其分為五類，劃分結果見圖8中的第9道。基于表6中每一類石灰巖儲層孔隙度與滲透率之間函數關系，可以計算得到每一類石灰巖儲層的滲透率。將所計算五類石灰巖儲層的滲透率進行組合，便能得到B井石灰巖儲層全井段的滲透率，從而達到定量評價B井石灰巖儲層滲透率的目的。

如圖8所示，在B井石灰巖儲層基于流動單元和分類算法耦合的滲透率評價成果圖中，第1道是自然伽馬測井曲線，表示該地層的巖性特征；第2道是體積密度、中子孔隙度和縱波時差測井曲線，反映該地層的物性特征；第3道是深、淺電阻率測井曲線，刻畫該地層的電性特征；第5道是基于上述測井曲線所計算的孔隙度與巖心分析的孔隙度；第6道是分類前，基于孔隙度所計算的滲透率與巖心分析的滲透率，二者誤差相對較大，平均絕對誤差為20.33mD；第7道是分類后，基于流動單元和分類算法耦合所計算的滲透率與巖心分析的滲透率，二者誤差相對較小，平均絕對誤差為7.37mD。

上述各實施例僅用于說明本發明，其中各部件的結構、連接方式等都是可以有所變化的，凡是在本發明技術方案的基礎上進行的等同變換和改進，均不應排除在本發明的保護范圍之外。