基于不確定連續屬性的決策樹分類器構建方法與流程
本發明涉及機器學習、人工智能以及數據挖掘領域,具體涉及一種基于不確定連續屬性的決策樹分類器構建方法。
背景技術:
決策樹研究是數據挖掘和機器學習中的一項重要和積極的研究課題。其所提出的算法被廣泛地應用于實際問題當中,如ID3,CART和C4.5,此類算法主要是研究準確率的問題。隨著科學技術的進步,近年來,不確定數據頻繁地出現在現實應用中,包括無線傳感器網絡、無線射頻識別、隱私保護等領域。其數據特點是數據值并非是確定的,即表示一個數據點,其表示方式是將多種取值作為一個整體,按照某種概率分布作為每個取值對應出現可能性,其越來越頻繁的出現促使相關的研究得到了廣泛關注和快速發展。而傳統數據挖掘技術中往往忽略了數據中的不確定性,其研究模型與客觀世界不符。所以不確定數據挖掘技術對數據挖掘技術的實際應用有著重要意義。屬性的不確定性包括離散屬性和連續屬性,在訓練和測試的過程中,為了保證有效的評估模型,驗證分類器的性能,數據集中的類別都是已知的。這里主要是針對于不確定連續屬性的分類與預測,另外由于測量儀器受精度的影響,采集的數據往往包含一定的誤差,不是完全準確的,為了提高不確定連續屬性的分類準確率,本發明提出基于不確定連續屬性的決策樹分類器構建方法。
技術實現要素:
針對于解決不確定連續屬性分類與預測的問題以及提高對其分類、預測的準確率問題,本發明提出了基于不確定連續屬性的決策樹分類器構建方法。
為解決上述問題,本發明是通過以下技術方案實現的:
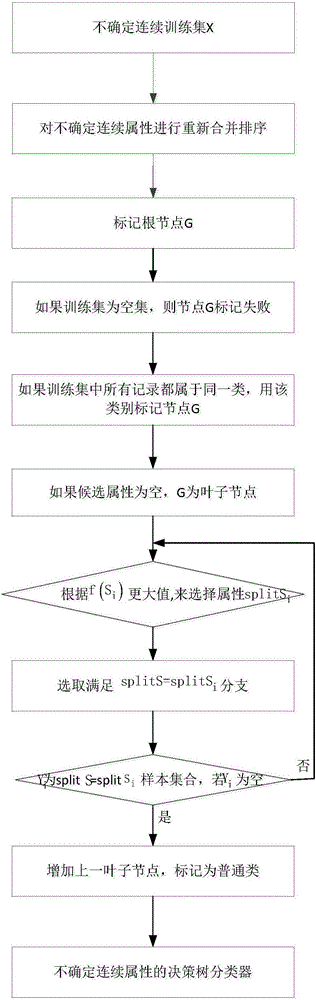
基于不確定連續屬性的決策樹分類器構建方法,包括如下步驟:
步驟1:設不確定連續屬性訓練集中有X個樣本,屬性個數為n,即n=(S1,S2,…Sn),同時分裂屬性Si對應了m個類L,其中Lr∈(L1,L2…,Lm),i∈(1,2…,n),r∈(1,2…,m)。Si∈(S1,S2,…Sn),其中屬性值具有連續不確定性。
步驟2:把不確定連續數據屬性Si的屬性值Sij合并排序,根據類對不確定性數據屬性Si進行屬性值Sij運算,記為概率和P(Sij),對類進行處理得每一分支屬性值的概率勢P(Sij,Lr)。
步驟3:創建根節點G。
步驟4:如果訓練數據集為空,則返回節點G并標記失敗。
步驟5:如果訓練數據集中所有記錄都屬于同一類別,則該類型標記節點G。
步驟6:如果候選屬性為空,則返回G為葉子結點,標記為訓練數據集中最普通的類。
步驟7:由于連續屬性值的不確定性,根據下面目標函數從候選屬性中選擇splitSi。
步驟8:標記節點G為屬性splitSi。
步驟9:由節點延伸出滿足條件為splitS=splitSi分支以及splitSi=splitSij子分支,如果滿足以下兩條件之一,就停止建樹。
9.1這里假設Yi為訓練數據集中splitS=splitSi的樣本集合,如果Yi為空,加上一個葉子結點,標記為訓練數據集中最普通的類。
9.2此節點中所有例子屬于同一類。
步驟10:非9.1與9.2中情況,則遞歸調用步驟7至步驟9。
步驟11:保存已生成的連續不確定性屬性的決策樹分類器。
本發明有益效果是:
1、構成的決策樹更好的規避了信息偏置為數量級大的問題。
2、可以實現對象為不確定連續屬性的歸類和預測功能。
3、此構建的決策樹分類準確度高。
4、此構建的決策樹更適用于對實際數據挖掘問題的應用。
附圖說明
圖1為基于不確定連續屬性的決策樹分類器構建流程圖。
具體實施方式
為解決不確定連續屬性分類、預測問題以及提高對其分類、預測的準確率問題,結合圖1對本發明進行了詳細說明,其具體實施步驟如下:
步驟1:設不確定連續屬性訓練集中有X個樣本,屬性個數為n,即n=(S1,S2,…Sn),同時分裂屬性Si對應了m個類L,其中Lr∈(L1,L2…,Lm),i∈(1,2…,n),r∈(1,2…,m)。Si∈(S1,S2,…Sn),其中屬性值具有不確定性。
步驟2:把不確定連續數據屬性Si的屬性值Sij合并排序,根據類對不確定連續數據屬性Si進行屬性值Sij運算,記為概率和P(Sij),對類進行處理得每一分支屬性值的概率勢P(Sij,Lr)。其具體運算過程如下:
不確定連續屬性Si,其取值P(Sij)為一個概率向量,記為:
P(Sij)∈(P(Si1),P(Si2),…,P(Sik)),且所以之前那些確定的連續屬性可以看作為這一特殊情況,即屬性Si中屬性值P(Sij)=1,其他概率為0的情形。
不確定連續屬性值在每個區間上都存在最大值和最小值端點。這種數值表示方式是出于保護客戶隱私為目的。不確定連續屬性的處理過程是將所有出現的關鍵點按升序排列,合并重復點,這樣屬性整個取值區間就被分割成多個子區間。
每個用例的取值區間會覆蓋一個或多個子區間。
假設任意一子集區間為[α,β],則其在區間[α,β]的概率分布為:
上式f(x)為此事件發生的概率分布,具體事件具體分析,這個由相應的專家確定,每個不確定連續屬性的概率分布函數普遍相同。
屬性Si在區間[α,β]的概率和P(Sij)為:
上式j∈(1,2,…,k),k為屬性Si對應的屬性值個數。
根據屬性值Sij對應的類Lr在區間[α,β]的概率勢P(Sij,Lr)為:
上式為屬性值Sij對應的類的種類,為在屬性值Sij對應的類中為Lr類。
P(Sij)為屬性值Sij根據類來取概率和,類L總共為m個。
步驟3:創建根節點G。
步驟4:如果訓練數據集為空,則返回節點G并標記失敗。
步驟5:如果訓練數據集中所有記錄都屬于同一類別,則該類型標記節點G。
步驟6:如果候選屬性為空,則返回G為葉子結點,標記為訓練數據集中最普通的類。
步驟7:由于連續屬性值的不確定性,根據下面目標函數f(Si)從候選屬性中選擇splitSi。其集體計算過程如下:
目標函數f(Si):
上式Lr∈(1,2,…,m),為Lr類。P(Sij)為步驟2中的屬性Si的概率勢,P(Sij,Lr步驟2中屬性Si的屬性值Sij關于類Lr的概率勢,j為屬性值個數。
當選擇屬性splitSi滿足目標函數f(Si)越大時,則找到標記節G。
步驟8:標記節點G為屬性splitSi。
步驟9:由節點延伸出滿足條件為splitS=splitSi分支以及splitSi=splitSij子分支,如果滿足以下兩條件之一,就停止建樹。
9.1這里假設Yi為訓練數據集中splitS=splitSi的樣本集合,如果Yi為空,加上一個葉子結點,標記為訓練數據集中最普通的類。
9.2此節點中所有例子屬于同一類。
分支葉子節點的確定先對比訓練集再由P(Sij,Lr)值大小確定,即
通過上式就可以確定葉子節點。
步驟10:非9.1與9.2中情況,則遞歸調用步驟7至步驟9。
步驟11:保存已生成的不確定連續數據的決策樹分類器。
基于不確定連續屬性的決策樹分類器構建方法,其偽代碼計算過程如下:
輸入:不確定連續數據訓練樣本集X。
輸出:不確定連續屬性的決策樹分類器。
- 還沒有人留言評論。精彩留言會獲得點贊!