一種改進的DIVRECT優化算法的制作方法

本發明涉及機電產品優化設計的
技術領域：
，特別是多輸入多輸出問題優化設計的
技術領域：

背景技術：
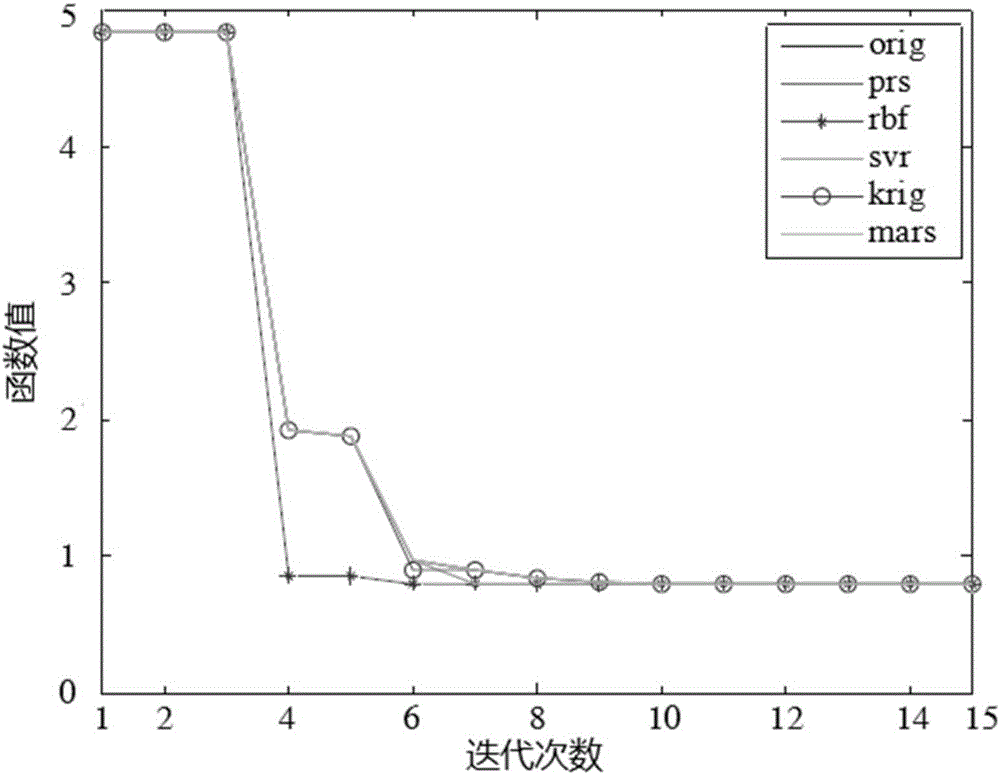
：細分矩形方法(DIVidingRECTangles,DIVRECT)作為一種全局優化算法，由DonaldR.Jones在1993年提出，它可以收斂并搜索到全局最佳點。DIVRECT算法將定義域當作一個n維超矩形，并對其進行不斷細分，然后根據每次迭代采樣點函數估值和細分情況決定搜索區域，直至搜索到全局最優解，因此非常適合于黑箱函數的優化仿真。DIVRECT方法是針對Lipschitz算法的不足而提出的，Lipschitz算法由于在搜索時必須取較大的常數而導致收斂速度緩慢。對于一個定義域為[a,b]區間的函數f(x)(見圖1)，若搜索函數全局最小值，Lipschitz方法是假設存在一Lipschitz常數K(此假設適用任意端點可估值閉區間)，滿足式：|f(x)-f(x')|≤K|x-x'|x,x'∈[a,b](1)如用m、n代替式(1)中x'，那么f(x)滿足式：f(x)≥f(m)-K(x-m)f(x)≥f(n)+K(x-n)(2)式(2)正好對應于圖1中的斜率-K和+K。若以X(m,n,f,K)表示f(x)最低點位置，對應值為B(m,n,f,K)，則有式：X(m,n,f,K)＝(m+n)/2+[f(m)-f(n)]/(2K)B(m,n,f,K)＝[f(m)+f(n)]/2-K(n-m)(3)式(3)作為Lipschitz算法的核心要素，其算法步驟首先從函數端點a和b搜索，然后估算x1＝X(a,b,f,K)函數值，因此將設計空間分為[a,x1]和[x1,b]，然后選擇擁有最小B值的區間進行下一步搜索，估算x2＝X(a,x1,f,K)處B值，此時將設計空間分為[a,x2]、[x1,x2]、[x1,b]三個區間，依次類推，每次迭代過程中的采樣點均在分段近似函數最小B值位置，因而可以不斷逼近函數f(x)，直至滿足終止標準。這種算法的缺陷在于：(1)Lipschitz算法強調全局搜索，從而導致收斂速度緩慢；(2)在初始化過程中對函數端點a和b估算，尤其是擴展到n維時需估算搜索空間的2n個頂點，因而進行優化過程中算法較復雜。為了克服Lipschitz算法缺點，相關文獻通過改進設計空間的分割方法提出DIVRECT算法。它著重強調對中心點而不是搜索空間的2n個頂點進行函數估值，用中心點q＝(m+n)/2表示[m,n]區間，令式(1)中參數x'值為q，則f(x)應滿足式：f(x)≥f(q)+K(x-q),x≤qf(x)≥f(q)-K(x-q),x≥q---(4)]]>目標函數則位于不等式斜率+K和-K交匯所構成圖形上方，下界函數式為：flow＝f(q)-K(n-m)/2(5)可以看出，其值只與區間中心點函數值有關。DIVRECT算法則把迭代過程采樣方式變為中心點采樣，并對所有潛在優化區域進行采樣，其算法步驟為：(1)設置c＝1，[m1,n1]＝[a,b]，q1＝(m1+n1)/2，并估算函數f(q1)值。設fmin＝f(q1)，令迭代初值t＝0，迭代次數為T；(2)識別哪些潛在區間為最優區間集S，并選擇任意區間j∈S；(3)令δ＝(nj-mj)/3，設qc+1＝qj-δ，qc+2＝qj+δ，對函數f(qc+1)和函數f(qc+2)估值并更新fmin；(4)對搜索區間進行細分，增加左右子區間：[mc+1,nc+1]=[mj,mj+δ][mc+2,nc+2]=[mj+2δ,nj]---(6)]]>其中，qc+1、qc+2為中心點，區間j設置為：[mj,nj]＝[mj+δ,mj+2δ](7)設c＝c+2；(5)設S＝S-{j}，如轉至步(2)；(6)設t＝t+1，若t＝T，停止搜索，否則轉至步(2)。對于多變量優化問題，則需要把一維DIVRECT算法擴展至多維，這樣搜索空間則轉化為n維超立方體單元，在搜索過程中，搜索空間被細分為更小的超立方體單元。但是，在設計域內DIVRECT算法需要多次采樣，才能保證搜索到全局最佳點，特別是優化后期，采樣點會越來越多，而且這些點為無效點，這樣造成收斂速度愈加緩慢。況且在實際優化中，目標模型一般較復雜，這樣優化算法往往很難被接受。實際上，在最佳點域內，DIVRECT算法假設目標函數是連續的，所以，可以利用最佳點域內的采樣點來構造精確的近似模型，這樣，即可加快算法收斂速度。元模型作為代理模型(Surrogate)，利用最小二乘回歸技術來實現二階多項式模型的擬合，可以通過實驗產生的采樣點來構造與源模型相近的數學模型代替源模型進行仿真優化分析，因而能節約計算資源，降低計算量。技術實現要素：為了解決現有技術中存在的缺陷，本發明提供了一種改進的DIVRECT算法。本發明提供的技術方案，一種改進的DIVRECT優化算法，其特征在于，包括以下步驟：步驟一：初始采樣：按照標準DIVRECT算法進行采樣；步驟二：識別潛在最優超立方體，函數估值；步驟三：識別最優域；步驟四：收集最優域內采樣點，獲取采樣點信息矩陣對應的函數值，構建元模型；步驟五：搜索最佳點，并進行函數估值，判斷該值是否為當前最優值；步驟六：判斷是否滿足收斂條件：如滿足則退出循環，否則轉向步驟二。優選方案，在步驟一中，標準DIVRECT算法具體步驟為：1)將搜索空間進行歸一化處理為單位超立方，設qi為中心點，并對函數f(q1)估值，同時，令fmin＝f(q1)，c＝1，迭代初值t＝0，迭代次數為T；2)識別潛在最佳超立方，放入集合S，并選擇任意超立方j∈S；3)細分超立方體，從超立方體j處采樣并對超立方體進行更小的子超立方體細分。更新fmin，令c＝c+Δc，Δc為新采樣點個數；4)設S＝S-{j}，如跳至步驟2)；5)t＝t+1，若t＝T，停止搜索，否則轉至2)。優選方案，在3)中，細分超立方體的具體步驟為：(1)設最長邊維度集合為M；(2)對點c+δei采樣并進行函數估值，其中，i∈M，c-超立方體中心點，ei-第i個單位向量；(3)沿M中維度細分包含點c的超立方體為3部分，先沿w值最小維度，然后再沿第二小w值細分，直到最大的wi值，其中，w＝min{f(c+δei),f(c-δei)}。優選方案，在步驟二中，識別潛在最佳超立方體的條件為：一超立方體細分為n個超立方體單元，設ai為第i個單元中心點，bi為中心點與頂點之間距離，若有δ＞0，使得超立方體j滿足優選方案，在步驟三中，識別最優域時首先定義超立方體區域密度式中，S-定義域內任一區域；V(S)-超立方體空間體積；-S域內采樣點；-采樣點個數，識別最優域算法步驟為：1)根據式求整個定義域內平均域密度找出函數值最小的當前采樣點，即為當前最佳點；2)求最佳點與非最佳點之間的歐氏距離，對非最佳點集進行排序；從集合當前位置cur算出點的坐標值，計算其與前一點間擴展區域；3)利用式求擴展區域密度ρi，如則為最優域并退出循環；4)令cur＝cur+1，如cur小于非最佳點集合個數，轉向2)，否則退出循環。優選方案，在步驟四中，構造元模型的方法為：1)選擇徑向基函數：選擇依據為目標函數的具體特征；2)采樣點的生成：收集最優域內的采樣點，然后對其進行函數估算，從而得到對應響應值；3)將m個采樣點xi及對應響應值f代入不同的徑向基函數得出線性方程組；4)對線性方程組求解，得出不同基函數對應權重系數λ＝[λ1,λ2,…,λn]T，再次將采樣點xi代入對應方程組即可得出元模型確切表達式。優選方案，在步驟五中，搜索最優點的方法：在元模型上調用Matlab的內置函數function進行，并對最優點調用源模型進行函數估值，如該值小于DIVRECT所有采樣點中最小的函數值，則該值為當前最優值；優選方案，在步驟六中，收斂條件下列三個條件其中之一：(1)當前最優值與預設目標優化值誤差小于δ；(2)三次迭代的最優值之差小于δ；(3)超過預設函數估值次數，其中，δ—預設極小數。相對于現有技術的有益效果，本發明通過對優化迭代過程中產生采樣點的數據分析，構建比較精確的元模型，從而達到提高收斂速度的目的。附圖說明圖1為本發明計算Lipschitz下限值示意圖；圖2為本發明布蘭函數優化過程對比圖；圖3為本發明六駝峰函數優化對比圖。具體實施方式需要說明的是，上述各技術特征繼續相互組合，形成未在上面列舉的各種實施例，均視為本發明說明書記載的范圍；并且，對本領域普通技術人員來說，可以根據上述說明加以改進或變換，而所有這些改進和變換都應屬于本發明所附權利要求的保護范圍。為了便于理解本發明，下面結合附圖和具體實施例，對本發明進行更詳細的說明。附圖中給出了本發明的較佳的實施例。但是，本發明可以以許多不同的形式來實現，并不限于本說明書所描述的實施例。相反地，提供這些實施例的目的是使對本發明的公開內容的理解更加透徹全面。一種改進的DIVRECT優化算法，其特征在于，包括以下步驟：步驟一：初始采樣：按照標準DIVRECT算法進行采樣；步驟二：識別潛在最優超立方體，函數估值；步驟三：識別最優域；步驟四：收集最優域內采樣點，獲取采樣點信息矩陣對應的函數值，構建元模型；步驟五：搜索最佳點，并進行函數估值，判斷該值是否為當前最優值；步驟六：判斷是否滿足收斂條件：如滿足則退出循環，否則轉向步驟二。優選方案，在步驟一中，標準DIVRECT算法具體步驟為：1)將搜索空間進行歸一化處理為單位超立方，設qi為中心點，并對函數f(q1)估值，同時，令fmin＝f(q1)，c＝1，迭代初值t＝0，迭代次數為T；2)識別潛在最佳超立方，放入集合S，并選擇任意超立方j∈S；3)細分超立方體，從超立方體j處采樣并對超立方體進行更小的子超立方體細分。更新fmin，令c＝c+Δc，Δc為新采樣點個數；4)設S＝S-{j}，如跳至步驟2)；5)t＝t+1，若t＝T，停止搜索，否則轉至2)。優選方案，在3)中，細分超立方體的具體步驟為：(1)設最長邊維度集合為M；(2)對點c+δei采樣并進行函數估值，其中，i∈M，c—超立方體中心點，ei—第i個單位向量；(3)沿M中維度細分包含點c的超立方體為3部分，先沿w值最小維度，然后再沿第二小w值細分，直到最大的wi值，其中，w＝min{f(c+δei),f(c-δei)}。優選方案，在步驟二中，識別潛在最佳超立方體的條件為：一超立方體細分為n個超立方體單元，設ai為第i個單元中心點，bi為中心點與頂點之間距離，若有δ＞0，使得超立方體j滿足優選方案，在步驟三中，識別最優域時首先定義超立方體區域密度式中，S—定義域內任一區域；V(S)—超立方體空間體積；—S域內采樣點；—采樣點個數，識別最優域算法步驟為：1)根據式求整個定義域內平均域密度找出函數值最小的當前采樣點，即為當前最佳點；2)求最佳點與非最佳點之間的歐氏距離，對非最佳點集進行排序；從集合當前位置cur算出點的坐標值，計算其與前一點間擴展區域；3)利用式求擴展區域密度ρi，如則為最優域并退出循環；4)令cur＝cur+1，如cur小于非最佳點集合個數，轉向2)，否則退出循環。優選方案，在步驟四中，構造元模型的方法為：1)選擇徑向基函數：選擇依據為目標函數的具體特征；2)采樣點的生成：收集最優域內的采樣點，然后對其進行函數估算，從而得到對應響應值；3)將m個采樣點xi及對應響應值f代入不同的徑向基函數得出線性方程組；4)對線性方程組求解，得出不同基函數對應權重系數λ＝[λ1,λ2,…,λn]T，再次將采樣點xi代入對應方程組即可得出元模型確切表達式。優選方案，在步驟五中，搜索最優點的方法：在元模型上調用Matlab的內置函數function進行，并對最優點調用源模型進行函數估值，如該值小于DIVRECT所有采樣點中最小的函數值，則該值為當前最優值；優選方案，在步驟六中，收斂條件下列三個條件其中之一：(1)當前最優值與預設目標優化值誤差小于δ；(2)三次迭代的最優值之差小于δ；(3)超過預設函數估值次數，其中，δ—預設極小數。基于此，本發明提出的改進的DIVRECT算法，通過對優化迭代過程中產生采樣點的數據分析，構建比較精確的元模型，從而達到提高收斂速度的目的。包括以下步驟：步驟一：初始采樣：按照標準DIVRECT算法進行采樣；步驟二：識別潛在最優超立方體，函數估值；步驟三：識別最優域；步驟四：收集最優域內采樣點，獲取采樣點信息矩陣對應的函數值，構建元模型；步驟五：搜索最佳點，并進行函數估值，判斷該值是否為當前最優值；步驟六：判斷是否滿足收斂條件：如滿足則退出循環，否則轉向步驟二。進一步的，在步驟一中，標準DIVRECT算法具體步驟為：1)將搜索空間進行歸一化處理為單位超立方，設qi為中心點，并對函數f(q1)估值，同時，令fmin＝f(q1)，c＝1，迭代初值t＝0，迭代次數為T；2)識別潛在最佳超立方，放入集合S，并選擇任意超立方j∈S；3)細分超立方體，從超立方體j處采樣并對超立方體進行更小的子超立方體細分。更新fmin，令c＝c+Δc，Δc為新采樣點個數；4)設S＝S-{j}，如跳至步驟2)；5)t＝t+1，若t＝T，停止搜索，否則轉至2)。進一步的，在3)中，細分超立方體的具體步驟為：(1)設最長邊維度集合為M；(2)對點c+δei采樣并進行函數估值，其中，i∈M，c—超立方體中心點，ei—第i個單位向量；(3)沿M中維度細分包含點c的超立方體為3部分，先沿w值最小維度，然后再沿第二小w值細分，直到最大的wi值，其中，w＝min{f(c+δei),f(c-δei)}。進一步的，在步驟二中，識別潛在最佳超立方體的條件為：一超立方體細分為n個超立方體單元，設ai為第i個單元中心點，bi為中心點與頂點之間距離，若有δ＞0，使得超立方體j滿足進一步的，在步驟三中，識別最優域時首先定義超立方體區域密度式中，S—定義域內任一區域；V(S)—超立方體空間體積；—S域內采樣點；—采樣點個數，識別最優域算法步驟為：1)根據式求整個定義域內平均域密度找出函數值最小的當前采樣點，即為當前最佳點；2)求最佳點與非最佳點之間的歐氏距離，對非最佳點集進行排序；從集合當前位置cur算出點的坐標值，計算其與前一點間擴展區域；3)利用式求擴展區域密度ρi，如則為最優域并退出循環；4)令cur＝cur+1，如cur小于非最佳點集合個數，轉向2)，否則退出循環。進一步的，在步驟四中，構造元模型的方法為：1)選擇徑向基函數：選擇依據為目標函數的具體特征；2)采樣點的生成：收集最優域內的采樣點，然后對其進行函數估算，從而得到對應響應值；3)將m個采樣點xi及對應響應值f代入不同的徑向基函數得出線性方程組；4)對線性方程組求解，得出不同基函數對應權重系數λ＝[λ1,λ2,…,λn]T，再次將采樣點xi代入對應方程組即可得出元模型確切表達式。進一步的，在步驟五中，搜索最優點的方法：在元模型上調用Matlab的內置函數function進行，并對最優點調用源模型進行函數估值，如該值小于DIVRECT所有采樣點中最小的函數值，則該值為當前最優值；進一步的，在步驟六中，收斂條件下列三個條件其中之一：(1)當前最優值與預設目標優化值誤差小于δ；(2)三次迭代的最優值之差小于δ；(3)超過預設函數估值次數，其中，δ—預設極小數。為驗證本發明提出的算法，采用布蘭(Branin)函數和六駝峰函數兩個例子進行驗證。(1)布蘭(Branin)函數：f(x)=(x2-5.14π2x12+5πx1-6)2+10(1-18π)cosx1+10,x1,x2∈[-5,10;0,15]]]>對比結果見表1和圖2，其中，orig表示原DIVRECT算法，PRS、RBF、SVR、KRIG、MARS表示基于不同元模型的DIVRECT算法。表1布蘭函數優化結果對比(2)六駝峰(six-humpcamel-back)函數f(x)=4x12-2.1x14+13x16+x1x2-4x22+4x24,x1,x2∈[-2,2;-2,2]]]>對比結果見圖3和表2。表2六駝峰函數優化結果對比從圖2、圖3可知，相比于原DIVRECT算法，新的DIVRECT算法能更快找到準確的全局最佳點，尤其是RBF元模型，在布蘭函數和六駝峰函數仿真中能顯著加快DIVRECT算法的收斂速度。從表1、表2可知，在函數估值次數對比中，尤其是RBF元模型的DIVRECT算法至少比原DIVRECT算法減少三分之二，效果非常明顯，這對于節約計算機資源，提高仿真優化效率具有重要意義。本發明公開了一種改進的DIVRECT優化算法，包括以下步驟：初始采樣；識別潛在最優超立方體，函數估值；識別最優域；收集最優域內采樣點，獲取采樣點信息矩陣對應的函數值，構建元模型；搜索最佳點，并進行函數估值，判斷該值是否為當前最優值；判斷是否滿足收斂條件。本發明針對標準DIVRECT算法在優化過程中不斷對中心點進行函數估值，因而迭代次數較多，并在不斷采樣過程中造成收斂速度緩慢等缺點，然后根據每次優化迭代產生的采樣點來構建元模型，并識別最優域，在最優域集合上搜索最優點，因而可以加快原DIVRECT算法的收斂速度，從而大大減少了計算工作量，降低了優化算法難度，節省寶貴計算資源，進而為工業設計中復雜機電產品結構優化設計提供一種新的思路與方法。當前第1頁1 2 3