一種滾動軸承表面損傷故障動力學建模方法與流程

本發明涉及一種滾動軸承故障動力學建模方法，特別涉及一種滾動軸承表面損傷故障動力學建模方法。
背景技術：
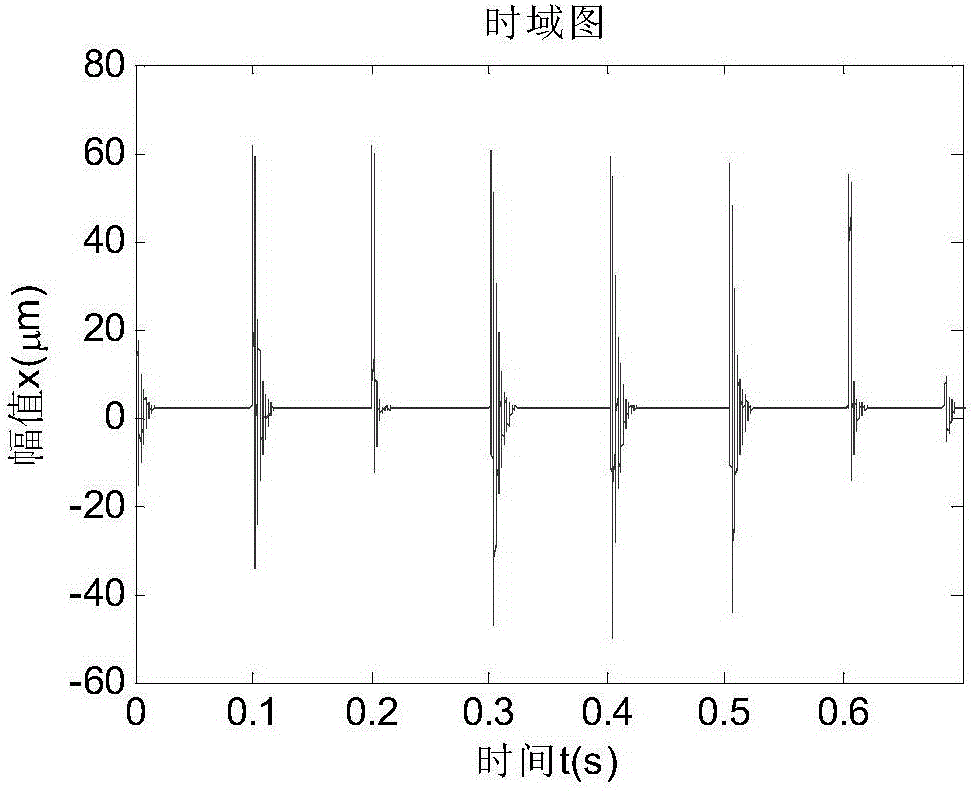
：滾動軸承故障診斷應用效果不佳的主要原因之一是缺乏滾動軸承故障機理研究。建立有效的、符合實際情況的滾動軸承故障動力學模型是滾動軸承故障機理研究的關鍵，也是滾動軸承故障診斷的技術基礎。針對滾動軸承故障動力學建模問題，眾多學者已開展了卓有成效的研究。張根源等基于單邊接觸和彈流潤滑理論模型對點缺陷滾動軸承的響應特征進行了分析，采用多體動力學方法建立了點缺陷滾動軸承動力學模型。徐東等通過對滾動軸承運轉過程中承壓滾子數變化規律的分析，建立了分段函數和缺陷沖擊函數模型。趙聯春等以深溝球軸承為對象，建立了軸承振動的彈性接觸模型，并以專門設計的試驗方法驗證了理論結果。陳於學等建立了早期缺陷非線性振動滾動軸承模型。東亞斌等建立了故障滾動軸承的等效模型。ZekiKiral等用力學模型結構模擬被軸承支座固定的故障軸承，并考慮不同位置缺陷對振動的影響。MatejTadin等考慮了在全局兩自由度中分析不同損傷位置的軸承振動特性。李昌等考慮潤滑油膜的接觸載荷與形變，運用ADAMS軟件對滾動軸承進行了動態虛擬仿真。但是在滾動軸承故障動力學建模未能有效地將故障沖擊融入到滾動軸承非線性動力學方程中，同時滾動軸承故障模型計算結果與仿真和實驗結果有較大出入，不能很好的應用于滾動軸承故障診斷。技術實現要素：為了解決上述技術問題，本發明提供一種高效高精度、計算結果準確的滾動軸承表面損傷故障動力學建模方法，它可以很好的為滾動軸承故障診斷提供技術支持。本發明解決上述技術問題的技術方案是：一種滾動軸承表面損傷故障動力學建模方法，步驟如下：1)在已獲得滾動軸承接觸等效剛度與等效阻尼的基礎上，考慮滾動軸承游隙以及承載區變化，建立滾動軸承彈簧阻尼振動模型；2)將表面損傷故障點的沖擊函數分別加載到外圈、內圈和滾動體上，分別建立滾動軸承外圈故障模型、滾動軸承內圈故障模型和滾軸軸承滾動體故障模型。上述的滾動軸承表面損傷故障動力學建模方法中，步驟2)中，滾動軸承內圈故障模型建立的具體步驟如下：根據公式(1)，計算第i個滾動體位置處的形變為δi，δi＝xcosθi+ysinθi-γ(1)式中：γ為滾動軸承的初始徑向間隙，θi是第i個滾動體與全局坐標x方向的夾角，x為內圈徑向x方向位移，y為內圈徑向y方向位移；沿x與y方向作用于內圈的外力，按公式(2)，公式(3)計算；Fx=KnΣi=1zλiδi1.5cosθi---(2)]]>Fy=KnΣi=1zλiδi1.5sinθi---(3)]]>Kn為單個滾動體與內外圈的接觸等效名義剛度，λi為第i個滾動體在負載區域的控制參數，Z為滾動體數量；內圈的運動方程如公式(4)所示：my··+cy·+Fy=wy+Id(t)sinψmx··+cx·+Fx=wx+Id(t)cosψ---(4)]]>m為內圈與轉軸的質量和，c為滾動體與內外圈相互作用的整體等效阻尼，wx、wy為負載作用在旋轉體上的徑向力，Id(t)為參數化的脈沖函數。在給定激勵的情況下，方程(4)是兩個耦合的非線性二階微分方程,將其無量綱化，滾動軸承的簡化方程如公式(5)所示：x‾··=1Knγ1.5(W+Id(t)cosΩτ)-cmvnx‾·-fx(x‾,y‾,Ω,τ)y‾··=1Knγ1.5Id(t)sinΩτ-cmwny‾·-fy(x‾,y‾,Ω,τ)---(5)]]>由于內圈表面損傷點的位置是隨內圈轉動而改變的，當損傷點的位置處于軸承的非承載區時，滾動體通過損傷點的振動影響可以忽略；損傷點處于承載區不同位置時，滾動體通過損傷點所產生沖擊力的大小不同；滾動體通過損傷點的角度為2arcsin(l/RI)，RI為內圈滾道直徑，l為損傷表面直徑；滾動體與損傷點表面相接觸角度為2arcsin(l/RI)，建立滾動體過損傷點的分段脈沖函數，如公式(6)所示：λ(υ)=1|υ|<arcsin(l/RI)0|υ|≥arcsin(l/RI)---(6)]]>當損傷點處于承載區并與滾動體相接觸時將產生沖擊，若處于非承載區時則不產生沖擊，建立承載區的分段脈沖函數，如公式(7)所示：s(v)=1|s|<L0|s|≥L---(7)]]>s為軸心位移方向與損傷點的夾角，L為滾子承載范圍角度的二分之一；對于不同的損傷有不同的表達，脈沖幅值的大小由負載和接觸點的速度所決定并且可以通過承載區的相對運動來函數化。滾動體與表面損傷的接觸時間是十分短的，因此在滾道上的損傷長度與軸承滾道長度的比例必須合適，這樣脈沖力才能與實際相符合，將脈沖函數代入滾動軸承的振動方程(5)中；由內圈損傷所產生的脈沖函數，其表達式如公式(8)所示：Id(t)=Aid(hid,L,ω)Σi=1zαid(i)·s(f(ψ,p(x)+arctan(y/|x|)))·λ(f(ψ,φi))---(8)]]>其中：hid為損傷點深度，φi為第i個滾動體質心與x軸正方向的夾角，ψ為軸承內圈上損傷點的位置與x軸正方向的夾角，ω為旋轉角速度；Aid(hid,L,ω)是關于損傷表面深度，長度及角速度的脈沖幅值函數關系式，aid(i)是第i個滾動體的幅值調制參數；f(ψ,p(x)+arctan(y/|x|))=mod(|ψ-arctan(y/|x|)|,2π)mod(|ψ-arctan(y/|x|)|,2π)≤π2π-mod(|ψ-arctan(y/|x|)|,2π)mod(|ψ-arctan(y/|x|)|,2π)>π,]]>式中：mod函數為求余函數；式中：Fr為滾動軸承徑向載荷，為第1個滾動體質心與x軸正方向的夾角，ε為徑向游隙。上述的滾動軸承表面損傷故障動力學建模方法中，步驟2)中，滾動軸承外圈故障模型建立的具體步驟如下：建立滾動體過損傷點的分段函數脈沖，如公式(10)所示：λ(υ)=1|υ|<arcsin(l/Ro)0|υ|≥arcsin(l/Ro)---(10)]]>υ為滾動體中心與損傷點中心的最小夾角；由外圈表面損傷所產生的脈沖函數，如公式(11)所示：Id(t)=Aid(hid,L,ω)Σi=1zαid(i)·λ(f(ψ,φi))---(11).]]>上述的滾動軸承表面損傷故障動力學建模方法中，步驟2)中，滾動軸承滾動體故障模型建立的具體步驟如下：根據公式(12)，計算滾動體的損傷點與x軸正方向的夾角，ψ＝ψ1-ωbt(12)ψ1為初始夾角，ωb為滾動體的自轉速度，t為時間；根據公式(13)，計算動坐標x軸正方向與絕對坐標x軸正方向之間的夾角，θx＝θx0+ωct(13)θx0為初始夾角，ωc為在絕對坐標中滾動體轉速，t為時間；根據公式(14)，計算滾動體上損傷點與外圈接觸的夾角，ψo＝ψ-θx(14)根據公式(15)，計算滾動體上損傷點與內圈接觸的夾角，ψi＝ψ-θx-180°(15)根據公式(16)，計算有損傷點的滾動體質心與x軸正方向的夾角；φ＝ωct+φ0(16)式中：φ0為軸承初始狀態下x軸與軸承正的第一個滾動體夾角；以x，y坐標軸為參考，根據公式(17)，計算滾子以逆時針方向與軸承位移的實時夾角；其中：建立滾動體過損傷點的分段函數脈沖，如公式(18)所示：λ(υ)=1|υ|<arcsin(l/r)0|υ|≥arcsin(l/r)---(18)]]>建立承載區的分段函數脈沖，如公式(19)所示：s(v)=1|s|<L0|s|≥L---(19)]]>建立由滾動體損傷所產生的沖擊函數，如公式(19)所示：其中：與現有技術相比，本發明具有以下有益效果：(1)本發明將表面損傷故障點的沖擊函數分別加載到外圈、內圈和滾動體上，建立滾動軸承外圈故障模型、滾動軸承內圈故障模型和滾軸軸承滾動體故障模型，更加符合實際情況，計算出的結果更為準確。(2)本發明的表面損傷建模，引入了承載區的分段函數和每個滾動體經過損傷表面的分段函數，來表征損傷點處于承載區不同位置時，滾動體通過損傷點所產生沖擊力的大小不同，具有簡單實用、計算準確的優點。附圖說明圖1為本發明的內圈故障模型。圖2為本發明的內圈故障x方向的振動信號時域圖。圖3為本發明的內圈故障x方向的振動幅頻圖。圖4為本發明的外圈故障模型。圖5為本發明的外圈故障x方向的振動信號時域圖。圖6為本發明的外圈故障x方向的振動幅頻圖。圖7為本發明的滾動體故障模型。圖8為本發明的滾動體故障x方向的振動信號時域圖。圖9為本發明的滾動體故障x方向的振動幅頻圖。圖10為本發明的內圈故障x方向振動加速度信號。圖11為本發明的內圈故障x方向振動加速度頻譜分析圖。圖12為本發明的外圈故障x方向振動加速度信號圖。圖13為本發明的外圈故障x方向振動加速度信號頻譜分析圖。圖14為本發明的滾動體故障x方向振動加速度信號圖。圖15為本發明的滾動體故障x方向振動加速度信號頻譜分析圖。圖16為本發明的內圈故障x方向振動信號分析圖。圖17為本發明的外圈故障x方向的振動信號分析圖。圖18為本發明的滾動體故障x方向的振動信號分析圖。具體實施方式下面結合附圖對本發明作進一步的說明。本發明的滾動軸承表面損傷故障動力學建模方法，包括如下步驟：1.滾動軸承內圈故障模型在考慮滾動軸承游隙的情況下，滾動體通過損傷點所產生沖擊力的大小會因損傷點處于承載區的不同位置而有所不同，忽略接觸表面的相對滑動，通過簡化可以將內圈運動視為兩自由度的質量彈簧阻尼系統。如圖1所示，負載通過軸加載在內圈上的效果力以及軸承局部表面損傷所產生的沖擊力均視為外載荷并作用于內圈上，第i個滾動體位置處的形變為δi，計算公式如公式(1)所示。δi＝xcosθi+ysinθi-γ(1)式中:γ為滾動軸承的初始徑向間隙，θi是第i個滾動體與全局坐標x方向的夾角，x為內圈徑向x方向位移，y為內圈徑向y方向位移。沿x與y方向作用于內圈的外力等于軸承承載分布力之和，計算公式如公式(2)，公式(3)所示。Fx=KnΣi=1zλiδi1.5cosθi---(2)]]>Fy=KnΣi=1zλiδi1.5sinθi---(3)]]>Kn為單個滾動體與內外圈的接觸等效名義剛度，λi為第i個滾動體在負載區域的控制參數，Z為滾動體數量。內圈的運動方程如公式(4)所示：my··+cy·+Fy=wy+Id(t)sinψmx··+cx·+Fx=wx+Id(t)cosψ---(4)]]>m為內圈與轉軸的質量和，c為滾動體與內外圈相互作用的整體等效阻尼，wx、wy為負載作用在旋轉體上的徑向力，Id(t)為參數化的脈沖函數。在給定激勵的情況下，方程(4)是兩個耦合的非線性二階微分方程[13],將其無量綱化，滾動軸承的簡化方程如(5)所示：x‾··=1Knγ1.5(W+Id(t)cosΩτ)-cmvnx‾·-fx(x‾,y‾,Ω,τ)y‾··=1Knγ1.5Id(t)sinΩτ-cmwny‾·-fy(x‾,y‾,Ω,τ)---(5)]]>內圈表面損傷點的位置是隨內圈轉動而改變的，當損傷點的位置處于軸承的非承載區時，滾動體通過損傷點的振動影響可以忽略。損傷點處于承載區不同位置時，滾動體通過損傷點所產生沖擊力的大小不同。這樣可引入承載區的分段函數和每個滾動體經過損傷表面的分段函數。滾動體通過損傷點的角度為2arcsin(l/RI)，RI為內圈滾道直徑，l為損傷表面直徑。滾動體與損傷點表面相接觸角度為2arcsin(l/RI)，建立滾動體過損傷點的分段脈沖函數，如(6)所示。λ(υ)=1|υ|<arcsin(l/RI)0|υ|≥arcsin(l/RI)---(6)]]>當損傷點處于承載區并與滾動體相接觸時將產生沖擊，若處于非承載區時則不產生沖擊，建立承載區的分段脈沖函數，如(7)所示。s(v)=1|s|<L0|s|≥L---(7)]]>式中：s為軸心位移方向與損傷點的夾角，L為滾子承載范圍角度的二分之一。對于不同的損傷有不同的表達，脈沖幅值的大小由負載和接觸點的速度所決定并且可以通過承載區的相對運動來函數化。滾動體與表面損傷的接觸時間是十分短的，因此在滾道上的損傷長度與軸承滾道長度的比例必須合適，這樣脈沖力才能與實際相符合，將脈沖函數代入滾動軸承的振動方程(5)中。由內圈損傷所產生的脈沖函數，其表達式如公式(8)所示。Id(t)=Aid(hid,L,ω)Σi=1zαid(i)·s(f(ψ,p(x)+arctan(y/|x|)))·λ(f(ψ,φi))---(8)]]>其中：hid為損傷點深度，φi為第i個滾動體質心與x軸正方向的夾角，ψ為軸承內圈上損傷點的位置與x軸正方向的夾角，ω為旋轉角速度；Aid(hid,L,ω)是關于損傷表面深度，長度及角速度的脈沖幅值函數關系式，aid(i)是第i個滾動體的幅值調制參數；f(ψ,p(x)+arctan(y/|x|))=mod(|ψ-arctan(y/|x|)|,2π)mod(|ψ-arctan(y/|x|)|,2π)≤π2π-mod(|ψ-arctan(y/|x|)|,2π)mod(|ψ-arctan(y/|x|)|,2π)>π,]]>式中：mod函數為求余函數。式中：Fr為滾動軸承徑向載荷，為第1個滾動體質心與x軸正方向的夾角，ε為徑向游隙。取參數Kn＝8.5941×109、m＝924.9g、γ＝0.00127mm、c＝484.026Ns/m、W＝9.06N、軸轉速為600rpm、初值取采用四階龍格庫塔計算方法求解，可得內圈x方向時域振動信號及其幅頻信號分別如圖2，3所示。從圖3中可以看出內圈轉頻為10.38Hz，內圈故障頻率的1倍頻為49.85Hz。引入滾動軸承變柔度頻率fvc即滾動體通過外圈某一定點時的頻率作為滾動軸承內圈徑向振動的基頻，計算公式如(9)所示。fvc=z2(1-dDcosα)fs---(9)]]>d為滾動體直徑，D為節圓直徑，α為接觸角，fs為內圈的旋轉頻率，將滾動軸承參數數據代入可求得變柔度頻率fvc＝3.05fs。從圖3可以看到轉速為600rpm時得到的理論計算fvc＝30.5Hz，與圖中所示的一階峰值的頻率基本相同，而且出現了倍頻關系。從內圈x方向上的頻譜中可以找到基頻30.46Hz與理論計算fvc幾乎一致，并且存在二倍頻關系，從而可以確定模型建立的正確性。2.滾動軸承外圈故障模型外圈故障模型如圖4所示。當損傷點的位置在外圈的承載區與滾動體相接觸時才會產生振動沖擊，因此損傷點一旦沒有處于承載區時，對軸承是不會產生沖擊力的。外圈產生的損傷點一般在其承載區，故外圈滾道表面損傷點產生沖擊力的頻率與滾動體經過外圈滾道損傷點的頻率相等。建立滾動體過損傷點的分段函數脈沖，如公式(10)所示：λ(υ)=1|υ|<arcsin(l/Ro)0|υ|≥arcsin(l/Ro)---(10)]]>υ為滾動體中心與損傷點中心的最小夾角。由外圈表面損傷所產生的脈沖函數，如公式(11)所示，外圈x方向時域振動信號及其幅頻信號分別如圖5，6所示。Id(t)=Aid(hid,L,ω)Σi=1zαid(i)·λ(f(ψ,φi))---(11)]]>從圖6中可以看出其外圈故障頻率為30.46Hz。3.滾動軸承滾動體故障模型滾動軸承的滾動體故障模型如圖7所示。假設滾動體與內外圈接觸時不產生相對滑移，其滾動體僅在xoy平面內作自轉與平移，這樣其表面的損傷點在一定時間內分別與內圈，外圈各接觸一次。根據公式(12)，計算滾動體的損傷點與x軸正方向的夾角：ψ＝ψ1-ωbt(12)式中：ψ1為初始夾角，ωb為滾動體的自轉速度，t為時間。根據公式(13)，計算動坐標x軸正方向與絕對坐標x軸正方向之間的夾角為，θx＝θx0+ωct(13)式中：θx0為初始夾角，ωc為在絕對坐標中滾動體轉速，t為時間。根據公式(14)，計算滾動體上損傷點與外圈接觸的夾角。ψo＝ψ-θx(14)根據公式(15)，計算滾動體上損傷點與內圈接觸的夾角。ψi＝ψ-θx-180°(15)根據公式(16)，計算有損傷點的滾動體質心與x軸正方向的夾角。φ＝ωct+φ0(16)式中：φ0為軸承初始狀態下x軸與軸承正的第一個滾動體夾角。這樣以x，y坐標軸為參考，根據公式(17)，計算滾子以逆時針方向與軸承位移的實時夾角。其中：滾動體過損傷點的分段函數脈沖為，λ(υ)=1|υ|<arcsin(l/r)0|υ|≥arcsin(l/r)---(18)]]>建立承載區的分段函數脈沖，s(v)=1|s|<L0|s|≥L---(19)]]>由滾動體損傷所產生的沖擊函數為，其中同理可得滾動軸承內圈x方向的振動信號時域圖及其幅頻圖分別如圖8、9所示。從圖9中可以看出滾動體故障特征頻率的1倍頻為39.46Hz。4.滾動軸承故障多體動力學仿真驗證根據實際滾動軸承尺寸建立滾動軸承三維實體模型如圖10所示。將滾動軸承支座簡化為彈簧-阻尼結構用來支撐外圈，滾動體通過設置好的接觸力分別與內外圈相接觸，滾動體與滾動體之間通過參數設置使其相互之間保持一定的角度，在分別在外圈、內圈和滾動體上設置損傷點模擬三種單故障的表面損傷沖擊振動。4.1滾動軸承內圈故障仿真內圈從靜止狀態開始旋轉，在0.3秒處達到3600rad/s穩定轉速，對其進行3秒鐘的仿真，內圈x方向的質心加速度時域圖及幅頻圖如圖11所示。內圈x方向振動加速度信號的時域圖通過共振解調分析后如圖11所示，從圖中可以看出內圈轉頻為10.09Hz，與模型計算值10.38Hz的偏差為0.29Hz，滾動軸承內圈的故障頻率的基頻為50.06Hz，與模型計算值49.5Hz偏差為0.46Hz，偏差的存在主要原因是由于軸承游隙，以及沖擊函數的影響。4.2滾動軸承外圈故障仿真內圈從靜止狀態開始旋轉，在0.3秒處達3600rad/s穩定轉速，對其進行1秒鐘的仿真，內圈x方向質心加速度時域圖及幅頻圖如圖12，13所示。從圖13中可以明顯看到倍頻關系，滾動軸承外圈故障特征頻率的基頻為30.15Hz，與模型計算值30.5偏差為0.35Hz。4.3滾動軸承滾動體故障仿真內圈從靜止狀態開始旋轉，在0.3秒處達3600rad/s穩定轉速，對其進行5秒鐘的仿真，內圈x方向的質心加速度時域圖以及幅頻圖如圖14、15所示。從圖15中可以明顯的看到滾動體的故障特征頻率的基頻39.56Hz與模型計算值39.62Hz偏差為0.06Hz，相鄰波峰差為3.70Hz，與滾動體公轉頻率的模型計算值3.81Hz偏差為0.11Hz。5.滾動軸承振動模型實驗驗證實驗裝置采用SpectraQuest公司(美國)的綜合故障模擬實驗臺，對帶內圈故障RexnordER10k滾動軸承進行振動信號采集。采集儀器為Brüel&公司的PULSELabShop平臺。在滾動軸承轉速為600rpm時，對x徑向進行加速度振動信號采集，對采集的原始振動信號直接進行FFT變換，這樣頻譜信號不會因消噪等信號處理方式使其固有的特征信號加入人為的干擾。通過實驗信號的頻譜處理分別得出x方向的內圈故障振動頻譜圖、外圈故障振動頻譜圖、滾動體故障振動頻譜圖，分別如圖18、19、20所示。從圖16中可以看到變柔頻率為30.4Hz與外圈故障基頻30.46Hz偏差為0.06Hz。內圈故障基頻為50.07Hz，與圖3中模型計算的內圈故障基頻49.85Hz偏差為0.22Hz，其2倍頻為100.4Hz。由于內圈故障響應相對于外圈故障響應的能量傳遞較弱，因此其信噪比相對較低，可以看出其除了特征頻率峰值外，均有大量的噪聲峰值。從圖17中可以看到其外圈的故障特征基頻為30.2Hz，與圖6中模型計算的特征基頻值30.46Hz偏差為0.26Hz，且同時出現尤為突出的2倍頻60Hz，圖中3倍頻90.6Hz幾乎被噪聲所淹沒。相對于內圈故障，外圈故障頻譜特征的信噪比在100Hz內是比較高的。從圖18中可以明顯的看到滾動體故障特征頻率的基頻為39.56Hz，與圖9中模型計算的基頻39.62Hz偏差為0.02Hz，其相鄰的波峰差為3.7Hz，與其滾動體公轉頻率的模型計算值3.81Hz偏差為0.11Hz。當前第1頁1 2 3