異構代價敏感機制決策樹構建方法與流程

本發明涉及機器學習、人工智能以及數據挖掘領域。

背景技術：

決策樹是數據挖掘和機器學習中的一項重要和積極的研究課題。其所提出的算法被廣泛地和成功地應用于實際問題中，如ID₃，CART和C4.5。現有算法之訓練決策樹分類器，旨在最大程度上提高分類的準確度，或最大限度地減少誤分類，但這必然會導致分類器偏向于主要的類而忽略罕見的或對精度影響較小的少數類。于是，在醫療診斷應用中，該反饋必然不符合數據挖掘的要求，因為在傳統決策樹方法的假設下，分布的類標記不平衡，并且所有分類錯誤造成的代價會被視為相同的成本。隨后，代價敏感決策樹學習算法引起了研究者們廣泛的興趣并取得了豐碩的研究成果。顯然構建一個適當的轉換不同代價單位的函數成為了挑戰，為此本文提出了一種有效的方法，此方法將減少所有不同代價所造成的代價機制和屬性的異質性。把所有不同的代價和屬性信息一起被納入分裂屬性選擇過程，并為此提供了一種異構代價敏感機制決策樹構建方法。

技術實現要素：

針對異構代價平衡性以及各種代價單位機制不同問題，提出了一種異構代價敏感機制決策樹構建方法。

本發明所采用技術方案：屬性S的目標函數f(S)為候選分裂屬性選擇因子，選取最大的f(S)值作為該節點候選分裂屬性，分支的分裂屬性選擇由gini(S_i)確定，即選取更小的gini(S_i)分支，加上一個葉子節點。循環執行上述操作，就可以遍歷整個訓練樣本集，得到強分類能力以及低誤分類代價和測試代價的決策樹。同時本文建樹過程中考慮了并解決了不同代價因子、各代價單位機制不同以及與信息純度之間的平衡性問題，所以此決策樹適應范圍更廣泛。

本發明有益效果是：

1、構建的決策樹有更好分類準確度，加強了分類能力

2、在決策樹構建過程中，標準化了誤分類代價和測試成本代價，解決了候選屬性誤分類代價和測試代價的不同單位機制問題，避免了候選屬性分裂選擇 的偏向大數量級屬性問題。

3、建樹過程中，很好的平衡由于測試代價和誤分類代價以及信息純度之間的存在的異構難題，把屬性分類能力和各種代價共同融合進候選分裂屬性選擇，得到了高的分類精度和降低誤分類代價和測試代價。

附圖說明

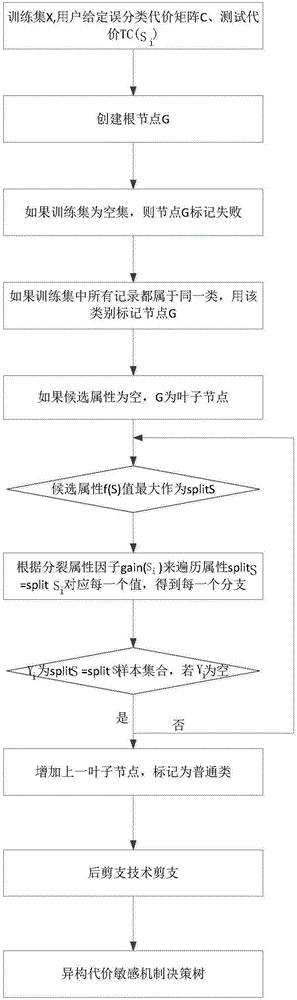
圖1為異構代價敏感機制決策樹流程圖

具體實施方式

為解決異構代價平衡性以及各種代價單位機制不同的問題，最后生成的決策樹更好的規避了過度擬合問題，本發明結合圖1進行了詳細說明，其具體實施步驟如下：

步驟1：設訓練集中有X個樣本，屬性個數為n，即n＝(S₁，S₂，…S_n),同時分裂屬性S_i對應了m個類L，其中L_r∈(L₁，L₂…，L_m),i∈(1，2…，n)，r∈(1，2…，m)。相關領域用戶設定好誤分類代價矩陣C、屬性測試代價為cost_i。

步驟2：創建根節點G。

步驟3：如果訓練數據集為空，則返回結點G并標記失敗。

步驟4：如果訓練數據集中所有記錄都屬于同一類別，則該類型標記結點G。

步驟5：如果候選屬性為空，則返回G為葉子結點，標記為訓練數據集中最普通的類。

步驟6：根據屬性S的目標函數f從候選屬性中選擇splitS。

目標函數f：

averagegini(S)為信息純度函數，TCration(S)為標準化測試代價比率函數，MCration(S)為標準化誤分類代價比率函數。

當選擇屬性splitS滿足目標函數f越大時，則找到標記結點G。

當出現目標函數f相等時，為打破平局標準，則按照下面的優先順序再進行選擇：

(1)更小的MCration(S)

(2)更小的TCration(S)

步驟7：標記結點G為屬性splitS。

步驟8：根據基尼指數gini(S_i)，由結點延伸出滿足條件為splitS＝splitS_i分支,如果滿足以下兩條件之一，就停止建樹。

8.1這里假設Y_i為訓練數據集中splitS＝splitS_i的樣本集合，如果Y_i為空，加上一個葉子結點，標記為訓練數據集中最普通的類。

8.2此結點中所有例子屬于同一類。

步驟9：非8.1與8.2中情況，則遞歸調用步驟6至步驟8。

步驟10：利用后剪支技術解決此決策樹模型中過度擬合問題。

步驟11：更新訓練數據集，保存新的示例數據。

以上步驟所涉及到的參數函數及定義，具體描述如下：

一、所述步驟1涉及到誤分類代價矩陣C、屬性測試代價為TC(S)

步驟1.1誤分類代價矩陣C

類別標識個數為m，則該數據的代價矩陣m×m方陣是：

其中c_ij表示第j類數據分為第i類的代價，如果i＝j為正確分類，則c_ij＝0,否則為錯誤分類c_ij≠0，其值由相關領域用戶給定,這里i，j∈(1，2，…，m)

步驟1.2屬性測試代價為TC(S)

TC(S)＝(1+cost_i)

其中cost_i為屬性S_i測試代價，這個由用戶指定。

二、所述步驟6求解目標函數，即f(S)，需求解信息純度函數averagegini(S)、標準化測試代價比率函數TCration(S)、標準化誤分類代價比率函數MCration(S)。具體求解過程如下：

步驟6.1：求解信息純度函數averagegini(S)

基尼指數是一種不純度分裂方法，基尼指數表示為gini(S_i)，定義為：

其中p(L_i/S_i)為類別L_i在屬性值S_i處的相對概率，當gini(S_i)＝0時，即在此結點處所有記錄都屬于同一類別，增加一葉子節點，即信息純度越大。反之，gini(S_i)最大，得到的有用信息最小，則繼續根據目標函數f(S)候選下一個屬性。

根據gini(S_i)可以得知averagegini(S)

這里屬性S有j個屬性值，即屬性值為(S₁，S₂，…，S_j)

信息純度函數averagegini(S)作用：可以提高決策樹的分類精度

步驟6.2：求解標準化測試代價比率函數TCration(S)

其中訓練集有n個候選屬性，即候選屬性為(S₁，S₂，…，S_n),S∈(S₁，S₂，…，S_n),TC(S_n)為候選屬性S_n測試成本。

TCration(S)函數作用：對測試成本進行標準化，避免了決策樹在歸納學習過程中偏向數量級更大的測試屬性，另外把不同單位代價機制轉化為同一單位代價機制。

步驟6.3：求解標準化誤分類代價比率函數MCration(S)

在分類代價基礎上，候選屬性S的標準化誤分類代價比率函數可表示為如下：

其中MC表示候選屬性分裂前的代價和，∑_{i∈classset(s)}MC(S)表示按候選屬性S分裂后的所有子類代價總和，其中classset(S)為候選屬性S分裂后的所有類的集合，根據具體例子，MC、∑_{i∈classset(s)}MC(S)可以很直觀的由用戶得出。

MCration(S)函數作用：對誤分類代價進行標準化，避免了決策樹在歸納學習過程中偏向數量級更大的測試屬性，另外把不同單位代價機制轉化為同一單位代價機制。

三、所述步驟10后剪支技術,具體求解過程如下：

后剪支條件為優先考慮到誤分類代價，然后考慮到測試代價，即對于用戶給定的正數α，β滿足下列兩條件，則實施剪支操作。

(1)MCration(S)＞α

(2)TC(S)＞β

剪支條件首先要滿足盡可能的使誤分類代價比率達到用戶指定條件，然后 足測試代價低到用戶要求。

偽代碼計算過程

輸入：X個樣本訓練集，訓練集的誤分類代價矩陣C，屬性測試代價為cost_i

輸出：異構代價敏感機制決策樹。