一種改進的布谷鳥搜索算法解決作業車間調度問題的制作方法

本發明涉及作業車間調度技術領域。

背景技術：

作業車間調度問題(Job-shop Scheduling Problem)是許多實際生產調度問題的簡化模型，具有廣泛的應用背景，譬如生產制造、交通規則、郵電通信、大規模集成電路設計等問題。作為一類滿足任務配置和順序約束要求的分配問題，JSP已被證明是一個典型的NP_hard問題，它的求解難度圓圓大于流水線調度問題。針對解決作業車間調度問題的算法一直是學術界和工程界共同關注的重要課題。

現有很多算法被用于解決JSP問題，包括遺傳算法、粒子群算法等，但沒有一種算法能夠直接將車間作業的屬性作為參數，最終得到一組明了的作業車間中生產調度方案解的算法。

布谷鳥搜索(Cuckoo Search,CS)算法是一種新的現代啟發式算法，由劍橋大學Yang和拉曼工程學院Deb于2009年提出的。該算法基于某些布谷鳥種類的巢寄生繁育行為和鳥類、果蠅等的萊維飛行(Levy flight)行為特征提出。布谷鳥搜索算法是模擬布谷鳥為尋找合適的產卵的鳥窩而隨機游走的尋窩過程。在這個宿主的選擇過程中，布谷鳥在繁殖期尋找與孵化期和育雛其相似的雛鳥食性基本相同、卵形與顏色易仿的宿主。多數情況下，宿主一旦識別出寄生卵，就將寄生卵扔出或棄巢，在其他地方另建新巢。而布谷鳥在下一次選擇宿主的時候也會放棄該鳥巢而重新選擇。為了便于模擬布谷鳥的尋窩方式，Yang和Deb提出了一下3個假設：(1)布谷鳥一次只產一個蛋，并隨機選擇鳥窩位置進行孵化；(2)在隨機選擇的一組鳥窩中，最好的鳥窩位置將被保留到下一代；(3)可利用宿主的鳥窩數量n是固定的，宿主發現一個外來鳥蛋的概率為Pa。Pa可以近似看作n個位置較差的鳥窩被隨機產生的幾個新鳥窩替換的概率，通常設Pa為一個固定值。

傳統的布谷鳥算法具有很好的全局最優搜索能力，算法參數少易于實現，但是該算法搜索速度不夠快，計算精度不夠高，算法應用范圍不夠大，搜索活力不足。

技術實現要素：

針對現有技術中存在的上述不足，本發明要解決的技術問題是提供一種改進的布谷鳥搜索算法解決作業車間調度問題。

本發明的目的是克服現有技術中存在的：傳統的布谷鳥搜索算法假設條件多，搜索速度不夠快，計算精度不夠高，算法應用范圍也不夠大，以及沒有一種算法能夠直觀地給出作業車間調度方案的算法。

本發明要實現的目標是：最小化最大完工時間。

本發明為實現上述目的所采用的技術方案是：一種改進的布谷鳥搜索算法解決作業車間調度問題。該算法的具體步驟如下：

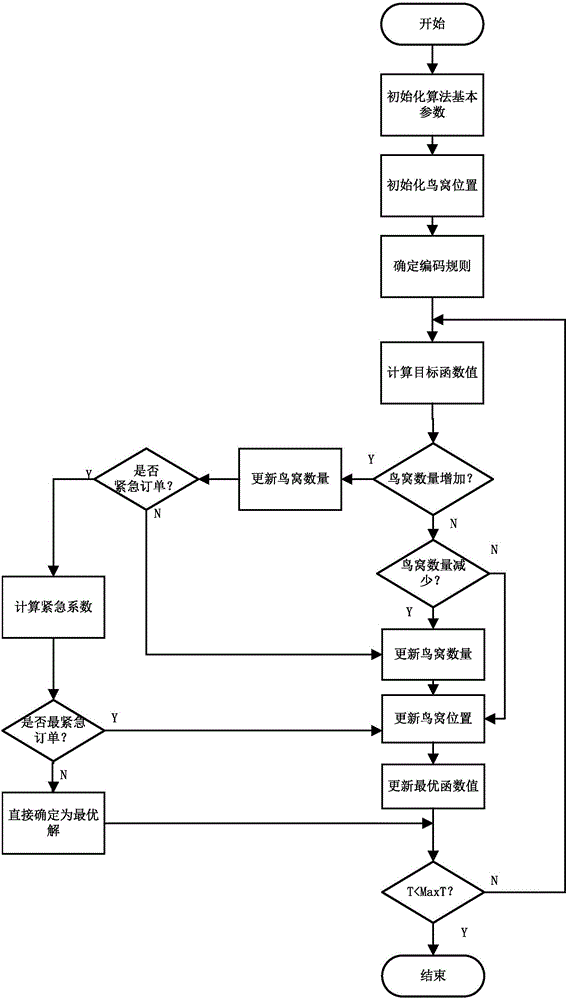
步驟1：初始化算法基本參數：設置鳥窩個數(工件數量)N,宿主發現外來鳥蛋的概率Pa(作業搶占概率)，以及最大迭代次數MaxT或搜索精度ε；

步驟2：初始化鳥窩位置(工件加工完成時間)：根據訂單周期T_o，訂單收益R，工件加工時間長度三個方面來確定鳥窩初始位置；

步驟3：確定編碼規則：按照編碼規則將鳥窩位置(完成時間)轉換為工序排列；

步驟4：計算目標函數值：計算各鳥窩位置對應的目標函數值，并獲得當前最優鳥窩位置；

步驟5：更新鳥窩位置：考慮了鳥窩數量變化的情況。增加，減少，以及增加的工件訂單是否為緊急訂單的情況；

步驟6：當到達最大搜索次數或滿足搜索精度時轉入步驟7，否則，轉步驟4進行下一次搜索。

步驟7：輸出最優調度值和對應的調度方案(染色體序列)。

本發明的有益效果是：

1、確定了布谷鳥算法中外來鳥蛋的計算方式，精確高效，使算法更加適用于實際生產環境中。

2、對于布谷鳥搜索算法在車間調度問題中的應用上，確定了鳥窩的初始位置的計算方式，使算法結果更加精確，同時計算方法簡單，方便高效，實用性高。

3、突破了布谷鳥算法的三個假設條件之一：鳥窩數量不變。本發明在考慮鳥窩數量增加的基礎上，考慮了鳥窩數量減少的情況，使算法的應用范圍更廣。

4、確定了訂單估計完成時間的計算方法。

附圖說明

一種改進布谷鳥搜索算法的基本流程圖

具體實施方式

為了使本發明的目的、技術方案及發明內容更加清楚，以下結合附圖詳細說明。

步驟1：初始化算法基本參數：設置鳥窩個數(工件數量)N,宿主發現外來

鳥蛋的概率Pa(作業搶占概率)，以及最大迭代次數MaxT或搜索精度ε：

其中，n為第L優先級的鳥巢(工件)數量；

步驟2：初始化鳥窩位置(工件加工完成時間)：根據訂單周期T_o，訂單收

益R，工件加工時間長度三個方面來確定鳥窩初始位置，具體方式如下：

其中，R為完成該訂單所獲收益，no為訂單o的工件數量；

步驟3：確定編碼規則：按照編碼規則將鳥窩位置(完成時間)轉換為工序排列，采用基于工序的編碼規則編碼，即染色體由w×n×m個基因組成，他們表示一個工序的排列，在這個工序排列中每個工件號最多出現m次，其染色體是由一個二維空間點(x,y)表示，即第x個訂單的第y個工件；例如，3×4×3(訂單×階數×工件×機器)的實例，染色體序列為(1,1)(1,2)(2,1)(1,1)(3,1)(3,1)(3,3)(3,2)(1,2)(1,2)(1,1)(1,4)。那么，它對應的工件加工序列為：

(J_1，1，1，J_1，2，1，J_2，1，1，J_1，1，2，J_3，1，1，J_3，1，2，J_3，3，1，J_3，2，1，J_1，2，1，J_1，2，2，J_1，1，3，J_1，4，1)，其中，J_ti，j表示第t個訂單的第i個工件的第j道工序，j表示工件i出現的次數。因此，上面例子的染色體序列表達的意思是先加工順序為：第1個訂單的第1個工件的第1道工序，加工第1個訂單第2個工件的第1道工序，在加工第2個訂單第1個工件的第1道工序，加工第1個訂單第1個工件的第2道工序，以此類推，最后加工第1個訂單第4個工件的第1道工序。因此在解碼時就可以按照工件的出現順序轉化為一個調度方案。

步驟4：計算目標函數值：計算各鳥窩位置對應的目標函數值，并獲得當前最優鳥窩位置，具體實現為：

目標函數：

f(T)＝min max_1≤o≤w{max_1≤k≤m{max_1≤i≤nT_oik}} (1)

約束條件：

T_oik-p_oik+M(1-a_oihk)≥T_oih

(o＝1，2，…，w；i＝1，2，…，n；h，k＝1，2，…，m) (2)

T_ojk-T_oik+M(1-x_oijk)≥p_oik

(i，j＝1，2，…，n；o＝1，2，…，w；k＝1，2，…，m) (3)

T_oik≥0(o＝1，2，…，w；i＝1，2，…，n)；k＝1，2，…，m) (4)

x_oijk＝0或1(i，j＝1，2，…，n；o＝1，2，…，w；k＝1，2，…，m) (5)

max_i{T_oi}≤T_o (6)

其中，式(1)表示目標函數，即完成時間(Makespan)；式(2)表示工藝約束條件決定的每個工件的操作的先后順序；式(3)表示加工每個工件的每臺機器的先后順序；式(4)表示完工時間變量約束條件；式(5)表示變量可能的取值大小，式(6)表示第o個訂單的所有工件最大完成時間小于訂單周期T_o的時間約束；上述公式中所涉及的符號定義含義如下：T_oik和p_oik分別為第o個訂單(或階數)中的第i個工件在機器k上的完成時間點和加工時間長度；M是一個足夠大的整數；a_oihk和x_oijk分別為指示系數和指示變量，其含義為：

步驟5：更新鳥窩位置：

(1)一種情況：如果沒有新的鳥窩出現(鳥窩數量沒有增加(沒有新的訂單的出現))：開始迭代，保留上代最優鳥窩位置不變，更新鳥窩位置(即全局搜索)，從而隨機產生下一代鳥窩，并評估位置更新后每個鳥窩的目標函數值，記錄當前最優鳥窩位置。具體實施方案如下數學公式所示：

其中，表示第i只布谷鳥在第t代的鳥窩位置(在車間調度問題中用C_oik表示)，α是步長大小參數，一般取α＝0.1。參數S是隨機游動的步長，計算公式如下：

S＝u+α·σ (10)

其中，

在局部搜索時對每一鳥窩位置按條件進行更新：用一個隨機數Ra作為鳥窩主人發現外來鳥蛋的概率并與Pa進行比較，若Ra>Pa，則隨機改變鳥窩位置，否則保持原來位置不變,并計算位置移動后每個鳥窩的目標函數值，記錄當前最優鳥窩位置，用如下0-1規劃模型表示：

(2)另一種情況：如果有新的鳥窩出現(有新的訂單出現)，鳥窩數量增加，即：N+H，H為新增的鳥窩數量，同時，判斷是否為緊急訂單：是，則做緊急訂單處理操作，把該訂單的工件設置為所需加工的工序的優先級，不是緊急訂單，則不做緊急處理。

緊急訂單處理操作如下：

計算緊急系數，緊急系數越大的訂單緊急程度越大，越需要得到優先處理，緊急系數的計算如下：

其中，max{To_pre}為訂單o的估計完成時間，其計算方式為：

max{To_pre}＝T_ave+α·R

其中，α∈(0，1)，實數，R為完成該訂單所獲收益，no為訂單o的工件數量；

當有鳥窩數量減少(有訂單還沒加工完就被迫撤離)的時候，直接定義N＝N-Z，其中，Z為減少的鳥窩數量，算法依舊依照上述算法執行；

步驟6：當到達最大搜索次數或滿足搜索精度時轉入步驟7，否則，轉

步驟4進行下一次搜索；

步驟7：輸出最優調度值和對應的調度方案(染色體序列)。