一種基于多維高斯云模型的巖爆等級評價方法與流程
本發明屬于地下工程技術領域,具體涉及一種基于多維高斯云模型的巖爆等級評價方法。
背景技術:
巖爆是深部巖體工程開挖或開采過程常見的一種地質災害,主要在高地應力條件下,由于巖體工程開挖卸荷引起圍巖內應力場重分布,導致硬脆性圍巖中儲存的彈性應變能突然釋放而產生爆裂、松脫、剝離、彈射甚至拋擲等破壞現象的一種動力失穩地質災害。巖爆的發生直接威脅作業人員和設備的安全,影響工程進度,甚至摧毀整個工程。隨著埋深的增加或應力水平的提高,我國地下工程的巖爆呈頻發趨勢。因此,巖爆的準確預測對于地下工程的安全和施工進度的保障顯得尤為重要。
近些年來,國內外在巖爆預測方面做了大量的研究,研究學者們從不同角度結合不同的理論數值分析方法對巖爆進行了預測研究。然而由于巖爆是一種非常復雜的非線性動力學現象,其發生機理復雜,具有模糊性和隨機性的特點。因此,現有分析方法難以對巖爆的發生與否及其烈度等級進行準確、快速的預測。
技術實現要素:
為了克服現有技術中存在的缺陷,本發明的目的在于提出一種基于多維高斯云模型的巖爆烈度等級預測方法,能夠客觀、準確、快速地評價深部地下工程的巖爆烈度等級。
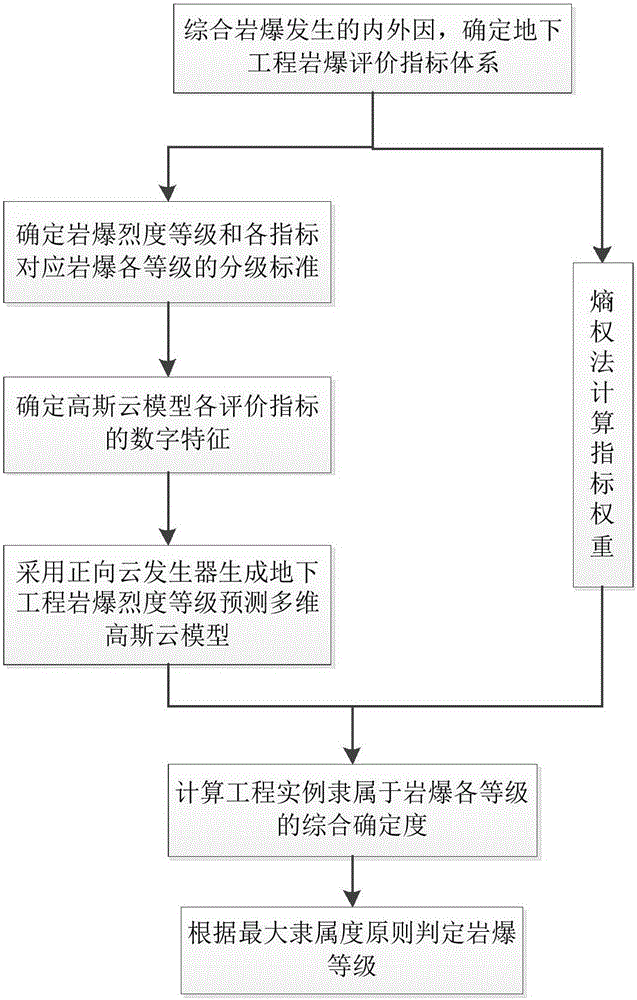
一種基于多維高斯云模型的巖爆等級評價方法,包括以下步驟:
步驟1:建立巖爆評價指標體系并確定巖爆等級的分級標準;
步驟2:求取步驟1中評價指標體系中各評價指標對應各巖爆等級的高斯云數字特征,并通過正向多維高斯云發生器生成多維高斯云模型;
步驟3:收集典型深部地下工程巖爆實例數據,構建豐富的訓練樣本庫,并采用熵權法,計算訓練樣本庫中各指標熵權,并以此作為深部地下工程巖爆評價過程中的各指標權重;
步驟4:將工程中各評價指標的實測值代入多維高斯云模型,并結合各指標的權重計算工程隸屬于各巖爆等級的綜合確定度;
步驟5:根據最大確定度原則判定工程的巖爆烈度等級;
所述步驟1中建立的巖爆評價指標體系中包含四個指標,分別為巖石單軸抗壓強度與抗拉強度比σc/σt、切向應力與巖石單軸抗壓強度比σθ/σc、彈性變形能指數Wet和巖石完整性系數Kv;
所述巖爆等級包括四個等級,分別為I級、II級、III級及IV級,依次對應為無巖爆、輕 微巖爆、中等巖爆和強烈巖爆;
所述巖爆等級的分級標準如表1所示:
表1巖爆預測指標分級標準
所述步驟2中多維高斯云模型的構建是根據確定的各評價指標的分級標準,確定各巖爆等級中評價指標預測云模型的期望(Ex1,Ex2,Ex3,Ex4)、熵(En1,En2,En3,En4)和超熵(He1,He2,He3,He4),通過運行多維正向高斯云發生器生成;
每一個巖爆等級下均有對應的評價指標預測云模型的期望、熵和超熵;
所述多維高斯云模型的期望的計算公式為:
多維高斯云模型的熵的計算公式為:
多維高斯云模型的超熵的計算公式為:He=K
式中:Cmax和Cmin分別為對應等級標準中對應評價指標的最大邊界值和最小邊界值,按照表1所示的巖爆預測指標分級標準獲取對應評價指標在對應某等級的上、下邊界值;當巖爆預測指標分級標準中評價指標無上邊界取值時,Cmax取實例中評價指標的倍作為上邊界取值;
K為反映云滴離散程度的常數,取值為En的0~1/3倍。
所述步驟4中結合各指標的權重計算工程隸屬于各巖爆等級的綜合確定度的計算公式如下:
其中,U為綜合確定度,x(x1,x2,x3,x4)為四個巖爆評價指標取值的集合,x1,x2,x3,x4分別對應σc/σt、σθ/σc、Wet和Kv四個評價指標,m為評價方法中的評價指標數量;j為評價方法中評價指標集合的下標;ωj為對應指標的熵權,根據熵權法進行求取;xj為巖爆評價指標取值,為已知值;Exj為相應巖爆等級下評價指標所對應的期望值,依據高斯云模型的期望公式計算得到;E′nj為對應巖爆等級下評價指標的正態隨機數,根據熵和超熵計算獲得。
每個巖爆等級均有一個綜合確定度。
所述步驟5中根據最大確定度原則判定工程的巖爆烈度等級是指若最大的兩個綜合確定度數值之差小于設定閾值,則判定工程巖爆等級隸屬于兩個綜合確定度中最大綜合確定度對應的等級。
云模型能夠通過數字特征期望Ex、熵En、超熵He實現不確定性概念的定性到定量的轉換。其中期望Ex表示概念在論域空間的中心值;熵En表示論域空間中可被定性概念接受的云滴的取值范圍;超熵He是熵En的熵,反映了云滴的離散程度。
云模型在分析巖爆問題的不確定性上具有以下優勢:1)同概率論相比,云模型考慮了模糊性;2)同模糊集合中用隸屬度表示模糊性相比,云模型考慮了隸屬度的隨機性;3)同粗糙集利用精確知識背景下的上、下近似兩個集合來度量不確定性,云模型考慮了背景知識的不確定性。高斯云是多種云模型中應用最為廣泛的一種,多維高斯云模型是一維高斯云模型的推廣,可以反映多維定性概念。鑒于此,本發明以不確定性人工智能思想為基礎,將多維高斯云理論運用到巖爆發生和烈度分級預測中,同時采用熵權法確定各評價指標的權重,提出了一種巖爆預測的多維高斯云模型。
有益效果
本發明提供了一種基于多維高斯云模型的巖爆等級評價方法,首先構建巖爆烈度等級評價指標體系,將巖爆分為多個等級并確定了分級標準;然后求取各指標對應各巖爆等級的高斯云數字特征并建立多維高斯云模型;廣泛收集多組重大深部工程巖爆實例建立豐富的訓練樣本庫,并采用熵權法結合編程技術求取評價指標集中各指標的熵權;將各評價指標的實測值代入多維高斯云模型,結合相應的權重計算得到隸屬于各巖爆等級的綜合確定度;最后根據最大確定度原則確定工程巖爆烈度等級。該方法能夠全面、客觀、準確地評價巖爆等級,評價結果客觀,為深部地下工程巖爆烈度分級預測提供一種全新方法。
其優點具體體現在以下幾點:
(1)本發明基于深部地下工程巖爆預測方面的最新研究成果,綜合考慮巖爆成因和特點,選取多個影響因素作為評價指標,建立了巖爆烈度等級判別的多指標評價方法,克服了因單一指標不能很好反映巖爆發生規律而導致判別結果準確性低的缺點;同時應用熵權法求取各評價指標的權重,有效避免了權重求取過程中人為主觀因素的影響,確保了本發明方法預測結果的可靠度;
(2)本發明使預測信息直觀可靠,運用多維高斯云模型可以生動直觀地刻畫巖爆概念的的模糊性與隨機性,將評價指標定量值與定性巖爆烈度等級概念科學合理地關聯到了一起,并將巖爆等級這一定性概念轉換為綜合確定度,實現了定性與定量的轉換,結果直觀、準確, 便于實際應用分析;
(3)本發明具有很好的繼承性,只要獲得深部地下工程的4個預測指標值,就可迅速、準確的對巖爆等級進行判定預測,在實際工程中具有一定的應用意義。
附圖說明
圖1為本發明所述方法的流程示意圖;
圖2為正向所謂高斯云發生器示意圖。
具體實施方式
下面結合附圖對本發明技術方案進行詳細說明,但是本發明的保護范圍不局限于所述實施例。本發明提供一種基于多維高斯云模型的巖爆等級評價方法,如圖1所示,按如下步驟進行:
步驟1:建立巖爆評價指標體系并確定巖爆等級的分級標準。
綜合考慮影響巖爆發生的多種因素,參考相關研究成果,選定巖石單軸抗壓強度與抗拉強度比σc/σt、切向應力與巖石單軸抗壓強度比σθ/σc、彈性變形能指數Wet和巖石完整性系數Kv四個定量化指標建立巖爆等級預測的評價指標體系,這4項指標相互獨立、互為補充,能夠比較完整地反映巖爆的特征,而且在實驗室或現場容易測試獲取,便于不同巖爆工程實例間的比較分析研究。同時,參考國內外學者的研究成果,依據巖體破壞形態、力學特征、聲學特征、破壞過程、破壞程度、塊體大小等表觀現象將巖爆劃分為四個等級:無巖爆(I級)、輕微巖爆(II級)、中等巖爆(III級)和強烈巖爆(IV級)。
在確定影響巖爆發生評價指標體系的基礎上,結合王元漢在《巖爆預測的模糊數學綜合評判方法》和周科平在《深部金屬礦山RS-TOPSIS巖爆預測模型及其應用》中的相關研究成果,獲得了巖爆烈度等級和各評價指標的關系,如表1所示:
表1巖爆預測指標分級標準
步驟2:求取各指標對應各巖爆等級的高斯云數字特征并建立多維高斯云模型。
本發明中多維高斯云模型的期望的計算公式為:
多維高斯云模型的熵的計算公式為:
多維高斯云模型的超熵的計算公式為:He=K
式中:Cmax和Cmin分別為對應等級標準的最大、最小邊界值;k為常數,可以根據變量的模糊閾度進行調整。
采用正向多維高斯云發生器(如圖2)生成巖爆烈度等級預測的多維高斯云模型。首先根據指標分級標準計算期望(Ex1,Ex2,Ex3,Ex4)、熵(En1,En2,En3,En4)和超熵(He1,He2,He3,He4),多維高斯云模型的數字特征如表2所示。
表2多維高斯云模型數字特征
然后生成以Ex(Ex1,Ex2,Ex3,Ex4)為期望值,En(En1,En2,En3,En4)為標準差的高斯隨機數x(x1,x2,x3,x4),生成以En(En1,En2,En3,En4)為期望,He(He1,He2,He3,He4)為標準差的正態隨機數En'(En1',En2',En3',En4');最后通過x(x1,x2,x3,x4)、期望(Ex1,Ex2,Ex3,Ex4)和熵(En1,En2,En3,En4)計算確定度,計算公式為:
則x(x1,x2,x3,x4)和U(x(x1,x2,x3,x4))為多維高斯云的一個云滴;迭代N次后產生N個云滴,即可生成多維高斯云模型。
步驟3:收集具有代表性的深部地下工程巖爆實例建立豐富的訓練樣本庫,采用熵權法,利用編程技術計算各指標的熵權,并以此作為深部地下工程巖爆評價過程中的各指標權重。
收集到20組具有代表性的巖爆工程實例(實例數據如表3所示),以此建立巖爆實例訓練樣本庫。
表3地下工程巖爆分析數據樣本庫
采用熵權法計算巖爆各評價指標權重的具體步驟為:
(31)設m個評價對象和n個評價指標中的第i個對象的第j個指標取值為xij,構造原始評價指標數據矩陣X=(xij)mxn,并對矩陣X進行數據歸一化處理。
對越大越優的指標,即效益型指標,歸一化公式為:
對越小越優的指標,即成本型指標,歸一化公式為:
(32)根據歸一化后的數據計算各評價指標熵值ej及偏差度dj,計算公式為:
dj=1-ej
(33)根據各評價指標熵值ej及偏差度dj計算各指標的權重,計算公式為:
Wj=dj/(n-Σej)
按照信息熵的基本原理,根據熵權法求權重的基本步驟編制相關計算程序計算樣本中各評價指標的權重,其中在歸一化數據時,σc/σt為越大越好型,采用效益型指標計算公式進行歸一化,其他三因子為越小越好型,成本型指標計算公式進行歸一化。按照上述步驟,編制計算程序,輸入樣本庫數據計算得到各評價指標的熵值、偏差度和熵權如表4所示。
表4各評價指標熵權
步驟4:將各評價指標的實測值代入多維高斯云模型,并結合步驟3中的權重計算工程隸屬于各巖爆等級的綜合確定度。
將工程實例中各評價指標的實測值代入上述多維高斯云模型中,并結合各指標權重計算得到工程實例隸屬于各巖爆等級的綜合確定度,計算公式為:
步驟5:根據最大確定度原則判定工程的巖爆烈度等級。
根據最大確定度原則判定工程的巖爆烈度等級,按照上述計算過程計算工程隸屬于各巖爆等級的綜合確定度(UI,UII,UIII,UIV),求出最大值Max(UI,UII,UIII,UIV),則最大值對應的等級即為工程巖爆烈度等級判定結果。若結果中最大的兩個綜合確定度數值比較接近,即|U1-U2|<b(本發明定義b=0.01),且最大的兩個綜合確定度均大于等于0.1,則判定該工程隸屬于U1和U2所對應的等級,但偏向于較大的確定度對應的巖爆等級。
以步驟3中所建立的樣本庫中典型巖爆工程實例進行本發明方法的可靠性檢驗,其中多維高斯云模型的數字特征如表5所示。
表5多維高斯云模型數字特征
把采用本發明方法的判別結果與RS-TOPSIS法的判別結果及實際巖爆等級進行對比分析,結果如表6所示。
表6巖爆烈度判別結果
注:*表示誤判
樣本庫中的巖爆實例回判結果顯示:本發明巖爆判別模型判別結果全部正確,表明多維高斯云模型用于巖爆烈度分級預測是可行的。同時可知,巖爆烈度是一個定性概念,在分級過程中受不確定因素影響,因此應用云數字特征可將巖爆烈度的模糊性和隨機性轉化為確定度這個定量值,結果便于工程應用。同時該發明具有很好的繼承性,即只要獲得深部地下工程的4個預測指標值,就可迅速、準確的對巖爆等級進行判定預測,在實際工程中具有一定的應用意義。
某鐵礦地層自上古生界到新生界較為齊全,三迭系地層分布廣泛,自古生代以來,經歷了多次構造運動,褶皺、斷裂均較發育,且具明顯的繼承性活動為其特征,礦體地應力復雜,目前采深已超過700m。因此,有必要對其進行巖爆預測,以采取相應的措施保障生產安全。
在室內巖石力學試驗、現場地應力測量及工程地質調查的基礎上,應用本發明建立的多維高斯云模型對該鐵礦-510m、-550m、-580m、-600m和-650m水平進行巖爆預測,判別結果如表7所示。
表7某鐵礦巖爆實測數據及判別結果
從現場的實際情況來看,巖爆初始發生在-530m水平階段,隨著開采深度越來越大,巖石的脆性不斷增加,巖爆現象時有發生,當開采到-600m水平時,巖爆呈大規模連續分布,并伴隨著聲響、振動和彈射現象,對生產已造成了威脅。對比本發明評價模型的判別結果和實際情況,結果顯示預測結果與工程實際吻合。由此可見,本發明中的基于多維高斯云模型的巖爆烈度分級預測是完全可行的,能比較客觀地反映巖爆問題的真實情況,具有一定的工程實際應用意義。
該方法具有簡單高效、準確率高、具有可繼承性等優點,可有效解決當前深部地下工程建設過程中巖爆地質災害預測效果不佳的問題。
以上所述,僅為本發明較佳的具體實施方式,本發明的保護范圍不限于此,本領域技術人員根據本發明的技術方案得出的其它的實施方式,同樣屬于本發明的技術創新范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!