基于二維激光傳感器的三維環境表面三角網格構建方法與流程

本發明涉及基于激光點云的環境建模領域，具體地說是一種基于二維激光傳感器的三維環境表面三角網格構建方法。

背景技術：

三維激光掃描技術是上世紀九十年代中期開始出現的一項高科技技術，它通過高速激光掃描測量的方法，大面積高分辨率地快速獲取被測對象表面的三維坐標數據，為空間信息的獲取提供了全新的技術手段。原始的三維激光點云數據缺少足夠的結構特征和語義信息，因此如何重構出與原激光掃描環境拓撲結構較為接近的環境模型成為人們重點關注的問題。網格構建是人們實現對三維環境表面模型的重建的方法，其中三角網格重構又是環境表面模型重建中使用最廣泛的一種方法，因為三角形是最簡單的多邊形并且具有構造靈活，邊界適應性好等優點，處理上也比較簡單，適用于對空間點云數據進行曲面重建。

當前較為常用的做法是對三維點云數據進行delaunay三角化，能夠快速的實現對三維激光點云數據的環境表面重建，α-shape、voronoi、crust算法、luigigiaccari的網格算法等算法都是在delaunay算法的基礎之上實現對三維激光點云數據的三角網格重構的。α-shape算法是刪除了四面體凸包中包圍球或外接圓半徑大于α的四面體來得到重建模型表面。“voronoi協方差”理論是基于voronoi圖計算過程中的一個協方差矩陣，得到點云曲面局部的主曲率和主方向，通過改變局部鄰域大小迭代計算協方差矩陣來提取特征點。crust算法是基于計算幾何中的voronoi圖和delaunay三角剖分。crust算法的優點就在于思想直接、簡單，重建效果更為精細，它可以對在細節區域具有密集點，在無特征或較少特征區域具有稀疏點的采樣點集實現曲線重建。luigigiaccari的網格算法是通過去除冗余三角面，提取模型表面三角平面的方法，該算法具有支持不規則的表面重構，能夠應用于多數情況下的開放表面。

這些經典的三維表面重建算法在處理均勻一致的三維激光點云數據時較為有效，但是由于激光掃描角度、掃描距離等原因，三維激光點云數據可能會出現點云數據不均勻或掃描面出現某種不連續的情況，這時上述經典算法很難構建出理想的三角化元素，甚至可能引入某些干擾的三角化元素，這將嚴重影響三角網格構建的效果。

技術實現要素：

針對現有技術的不足，本發明提供一種基于二維激光傳感器的三維環境表面三角網格構建方法，能夠重構出與原環境拓撲結構較為接近的三角網格，有效的避免了網格中三角化元素交叉錯亂和干擾等缺陷。

本發明為實現上述目的所采用的技術方案是：

一種基于二維激光傳感器的三維環境表面三角網格構建方法，包括以下步驟：

步驟1：二維激光傳感器采集三維環境掃描的掃描數據，并發送到上位機；

步驟2：將采集到的掃描數據轉換為笛卡爾空間坐標下的三維激光點云矩陣；

步驟3：將得到的三維激光點云矩陣根據均勻采樣法進行數據壓縮，得到三維激光點云數據；

步驟4：對三維激光點云數據進行三角網格構建。

所述均勻采樣法為從第一組單次掃描數據開始，每過掃描時間t取一組單次掃描數據，每次掃描的點云數一定，根據測量點的掃描順序，從單次掃描的起始點開始，每隔num個點記錄一個掃描點的掃描數據。

所述掃描數據包括轉動角度和距離值，其中轉動角度包括偏置角和關節角；

偏置角為：激光傳感器的掃描射線在激光掃描平面上的偏轉角度θ；

激光傳感器坐標系的xs'軸與pos'的夾角θ，其中pos'為掃描點p與激光傳感器坐標系原點os'的連線。

關節角為：激光傳感器在豎直方向上俯仰轉動的角度ψ；

距離值為：掃描點p到激光傳感器坐標系原點os的距離l，即pos'的長度為l。

所述三角網格構建包括以下過程：

步驟1：三維激光點云數據是按照點云矩陣的形式保存的，對點云矩陣中的數據點進行編號，點云矩陣p中第i行第j列的點表示為pi,j；

步驟2：對點云矩陣的m×n個數據進行劃分，得到(m-1)×(n-1)個小的點云矩陣；

步驟3：劃分后的每個點云矩陣包含四個點云數據，采用連接對角線方式對其劃分，完成三角網格構建。

所述對點云矩陣的m×n個數據進行劃分過程為：點云矩陣共有m行，相鄰兩行劃分為一組，則共可劃分為m-1組；每組共有n列，每相鄰兩列再次劃分為一組，則共可以劃分為n-1組，得到(m-1)×(n-1)個點云矩陣。

所述連接對角線方式為第一行的第二個點與第二行的第一個點相連接。

本發明具有以下有益效果及優點：

1.本發明適用范圍廣，能夠適用于多數的三維激光點云數據的環境建模。

2.本發明針對性強，能夠很好的處理激光點云數據的不均勻或者掃描面不連續的情況。

3.本發明處理效果好，能夠很好的重構出于原掃描環境拓撲結構相近的三角網格。

4.本發明原理簡單，處理速度快。

附圖說明

圖1為本發明的方法流程圖；

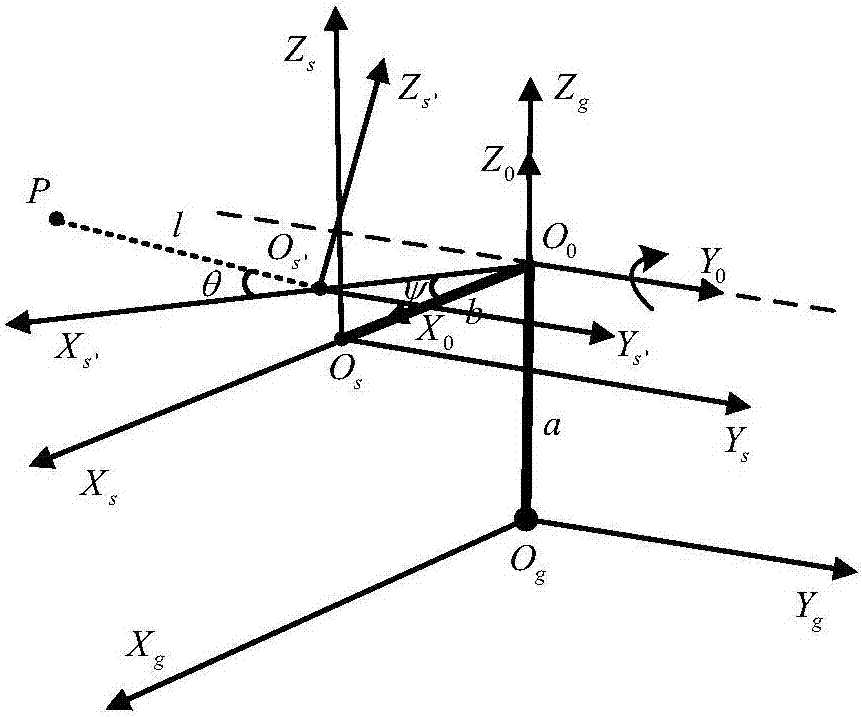
圖2為本發明的激光點云數據坐標系變換圖；

圖3為本發明的三維激光點云圖；

圖4為本發明的三維激光點云按行首次分組圖；

圖5為本發明的三維激光點云按列再次分組圖；

圖6為本發明的對點陣qt進行三角形構建圖；

圖7為本發明的最終的三角網格圖。

具體實施方式

下面結合附圖及實施例對本發明做進一步的詳細說明。

本發明的實現原理是：首先利用一維俯仰轉動云臺和二維激光傳感器搭建了三維激光掃描儀，并建立笛卡爾空間下的直角坐標系。利用上位機軟件記錄二維傳感器的掃描數據和一維俯仰轉動云臺的轉動角度值。再通過坐標變換實現上位機所記錄距離值、偏轉角度值和俯仰角度值到三維空間直角坐標系的變換并利用均勻采樣法實現對三維點云數據的壓縮。對壓縮后三維點云數據進行編號將其變成點云矩陣，為了實現點云矩陣的三角網格劃分首先對點云矩陣進行按行分組操作，然后再進行按列分組操作，則點云矩陣被劃分成了多個只有四個點云數據的小型點云矩陣。取任意一個小點云矩陣，連接對角頂點，形成對角線，從而構建出了兩個三角形網格。遍歷所有四個點的小型點云矩陣，連接相同位置的對角頂點最終實現對三維環境表面的三角網格構建。

如圖1所示為本發明的方法流程圖。

其步驟如下：

(1)由二維激光傳感器和一維俯仰轉動云臺構成三維激光掃描儀，結合上位機構成三維激光掃描系統。

(2)上位機軟件通過以太網實現與二維激光傳感器的通訊，通過can總線實現與一維轉動云臺的數據通訊。上位機從二維激光傳感器獲取三維環境掃描的掃描數據并同步記錄一維俯仰轉動云臺的俯仰角度值。

(3)通過坐標變換將采集到的數據轉換成笛卡爾空間坐標系下的三維激光點云數據。

(4)適當的進行點云數據的壓縮處理，以減少因點云過密而大量消耗的時間和資源。

(5)對經過步驟(4)處理過后的三維激光點云數據進行三維環境表面的三角網格構建。

如圖2所示為本發明的激光點云數據坐標系變換圖。所述步驟(1)的實現方法為：

1)由云臺支架和一維轉動模塊組成一維俯仰轉動云臺，將此云臺安裝在基座上。

2)以地面為xgogyg平面，建立三維場景基坐標系{xg,yg,zg}。此時的zg軸與一維俯仰轉動云臺的轉動模塊的水平轉軸交于o0點，yg軸平行于轉動模塊的水平轉軸，xg軸的正方向指向二維激光傳感器即將安裝位置的方向。

3)以o0點為原點建立直角坐標系{x0,y0,z0}。此時的x0軸平行于xg軸，y0軸平行于yg軸，z0軸與zg軸重合。

4)將二維激光傳感器安裝在一維俯仰轉動云臺上。以二維激光傳感器的掃描面為xsosys平面，建立二維激光傳感器坐標系{xs,ys,zs}。則此時的xs軸與x0軸重合，ys軸平行于y0軸，zs軸與z0軸平行。

所述步驟(2)的實現方法為：

1)安裝完成三維激光掃描儀后，以此時的三維激光掃描儀的位置為初始位置，則此時的俯仰角度值ψ為0°，此位置時某激光掃描點到二維激光傳感器坐標系原點os的距離為l。

2)上位機軟件啟動記錄之后，同步記錄下激光掃描點的距離值l、偏置角度θ和相應的俯仰角度值ψ，將這些的數值分別保存到三個文件中。同一俯仰角度時，只記錄一組掃描點數據。當俯仰角度值ψ變化后，記錄一組二維激光傳感器產生的距離值l，并同步記錄下與之對應的偏置角度值θ。

所述步驟(3)的實現方法為：

1)當俯仰角度值為ψ時，建立此時的二維激光傳感器坐標系{xs',ys',zs'}。坐標系{xs',ys',zs'}即為坐標系{xs,ys,zs}轉動ψ角度后的坐標系。

2)計算二維激光掃描點在二維激光傳感器坐標系{xs',ys',zs'}下的直角坐標值。當俯仰角度為ψ時某掃描點p的到原點os'距離值為l，偏置角度為θ，則點p在{xs',ys',zs'}下的直角坐標為：

3)通過坐標變換求取二維激光掃描點在基座標系下的直角坐標值。設a為轉動模塊水平轉軸y0到yg的距離；o點是y0軸與xs軸的交點，設b為oos的長度。則p點在基座標系{xg,yg,zg}下的坐標值為：

所述步驟(4)的實現方法為：

1)通過記錄的點云數據，從第一組單次掃描數據開始，每過時間t取一組單次掃描數據，并記錄下這組數據，刪除其余的未記錄的點云數據。

2)在步驟1)的基礎之上，再次減少點云數量。二維激光傳感器的掃描時間固定，單次掃描的產生點云數是固定的，根據記錄掃描點的掃描順序，從單次掃描的第一個掃描點開始，每隔num個掃描點記錄一個掃描點數據，刪除其余未記錄的點云數據。

所述步驟(5)的實現方法為：

1)三維激光點云數據是按照點云矩陣的形式保存的，對點云矩陣中的數據點進行編號，點云矩陣p如下：

其中，元素pi,j＝xi,ji+yi,jj+zi,jk(i＝1,2…,m；j＝1,2…,n)表示上位機記錄的激光傳感器的第i次掃描的第j個掃描點。如圖3所示為三維激光點云圖。

2)點云矩陣p中共有m×n個數據，對點云矩陣進行劃分。點云矩陣共有m行，相鄰兩行劃分為一組，則共可劃分為m-1組，如圖4所示為本發明的三維激光點云按行首次分組圖。

每組共有n列，每相鄰兩列再次劃分為一組，則共可以劃分為n-1組，如圖5所示三維激光點云按列再次分組圖。點云矩陣經過兩次劃分可以劃分為(m-1)×(n-1)個小組。則有

其中，

qt＝q(i-1)(n-1)+j＝{pi,j,pi,j+1,pi+1,j,pi+1,j+1}(i＝1,2…,m-1；j＝1,2…,n-1)

3)經過步驟2)，點云矩陣p被劃分成了(m-1)×(n-1)個小的點云矩陣，每個點云矩陣中有四個點云數據。為實現三角網格構建，對其進一步劃分，采用連接對角線方式對其劃分。第一行的第二個點與第二行的第一個點相連接，實現對單個小組的三角形劃分，如圖6所示本發明的對點陣qt進行三角形構建圖。遍歷集合q中所有的元素，共構建2(m-1)(n-1)三角形，則點云矩陣p可構建成含有2(m-1)(n-1)個三角形的三角網格，如圖7所示為本發明的對點陣qt進行三角形構建圖。

本發明未詳細說明內容為本領域技術人員公知技術。