基于數字巖心的水淹層新飽和度模型建立方法與流程
本發明涉及一種石油勘探開發行業測井領域中的一種飽和度評價方法,具體的說是一種新的水淹層飽和度模型的建立方法。
背景技術:
水淹層測井飽和度評價是油田開發過程中的一項重要技術,如何提供可靠的測井飽和度解釋結論一直是測井分析人員不斷探索解決的一個難題。而對于不同地質條件下水淹狀況的復雜性又給測井飽和度評價增加了難度。水淹復雜情況在一定程度上影響決策者開采方案的設計、實施及開發效果。因此,有必要開展水淹層測井飽和度解釋研究,建立更符合真實水淹機理的飽和度模型,這也是注水開發長期穩產高產,提高油田最終采收率的一項關鍵技術。
目前對水淹層飽和度模型主要集中在兩大類方法上:一類是并聯電阻率模型,另一類是基于離子交換與物質平衡方程的電阻率模型。并聯電阻率模型采用水淹層巖石體積模型構建,將水淹層巖石體積劃分為不同組分,假設各個組分是并聯導電從而計算巖石電阻率;基于離子交換與物質平衡方程的電阻率模型假設離子之間進行相互交換,進而計算不同含水飽和度下混合液礦化度,得到混合液電阻率,從而計算巖石電阻率。
對于并聯電阻率模型,最簡單模型為注入水與原始地層水完全獨立,以并聯方式導電,導電公式如下:
式中,rz為混合液電阻率,sw為地層中含水飽和度,swi為束縛水飽和度,rwi為束縛水電阻率,rwj為注入水電阻率。
該并聯模型完全將注入水與原始地層水獨立,并沒有考慮兩者之間離子交換作用,而且無法表示淡水水淹地層電阻率“u”型或者“s”型的特征。申輝林等人引入注入水倍數參數,將注入水體積與相滲曲線結合,其并聯模型為:
式中,v1為束縛水體積,v2為注入水體積,v為束縛水與注入水體積之和。該并聯模型可以表示出淡水水淹地層電阻率“u”型或者“s”型的特征,但該水淹層巖石體積物理模型并聯過程中把從地層中產出的水也計算在內,不符合實際情況。
第二類電阻率計算模型是基于離子交換與物質平衡方程的電阻率模型。鄒長春等人根據兩種溶液混合前后的離子數不變的原理,提出了計算混合液平均礦化度進而得到混合液電阻率的公式:
vc=v1c1+v2c2
式中,c1、c2分別是第一、二種溶液的礦化度;c是混合液礦化度。在特定的溫度下,溶液的電阻率與礦化度之間具有一一對應的關系,利用這種關系可以有效地計算混合液電阻率。但該水淹層巖石體積物理模型假設兩種混合液完全混合,與真實水淹機理相差較大。
無論是并聯電阻率模型還是基于離子交換與物質平衡方程的電阻率模型,有兩點水淹機理沒有考慮:一是注入水與原始地層水會發生離子交換,但由于接觸程度不同,注入水并不能完全接觸所有束縛水,兩種溶液并不是完全融合;二是水淹層巖石體積物理模型中注入水體積應為孔隙中自由流動的注入水體積,而不是總體積。為了得到更符合實際的水淹層飽和度模型,提高飽和度測井解釋的精度,必須要考慮上述真實的水淹機理。
技術實現要素:
本發明的目的就是針對目前水淹層飽和度模型水淹機理與實際條件相差較大、飽和度計算精度較低的問題,提供一種基于數字巖心技術進行水淹機理分析,得到不同注入水礦化度下電性規律,可以獲得更加準確的測井解釋水淹層飽和度,為儲層評價提供有力幫助的基于數字巖心的水淹層新飽和度模型建立方法。
其技術方案是:基于數字巖心的水淹層新飽和度模型建立方法,首先根據注入水先與大孔隙表面的薄膜束縛水接觸,后與小孔隙束縛水接觸,給出大孔隙薄膜束縛水和小孔隙束縛水的漸進混合式水淹層巖石體積物理模型,然后構建水淹層數字巖心,基于數字巖心技術進行水淹機理分析,得到不同注入水礦化度下電性規律,并得出不同注入水礦化度下電性規律計算公式,最終構建水淹層新飽和度模型。
基于數字巖心的水淹層新飽和度模型建立方法,包括以下步驟:
a.建立新等效水淹層巖石體積物理模型
根據注入水先與大孔隙表面的薄膜束縛水接觸,后與小孔隙束縛水接觸,將地層束縛水分為大孔隙薄膜束縛水swi1和小孔隙束縛水swi2,新等效水淹層巖石體積物理模型包括五部分:巖石骨架、剩余油、大孔隙薄膜束縛水、小孔隙束縛水、孔隙中注入水;
b.構建水淹層數字巖心
通過ct掃描法或數值模擬方法構建水淹層數字巖心;
c.基于數字巖心技術進行水淹機理分析,確定不同注入水礦化度下電性規律,并得出不同注入水礦化度下電性規律計算公式
首先需要確定束縛水分布:采用格子boltzmann方法,得到數字巖心中流體流速分布,當孔隙中流體流速為零時,認為該部分孔隙為束縛水;束縛水位置不變,采用數學形態法確定孔隙內其它位置的流體分布,進而得到不同含水飽和度下巖心流體分布;
然后在電性計算輸入參數時,將束縛水分為兩部分,一部分為注入水直接接觸到的大孔隙束縛水,另一部分為與注入水較遠或未接觸到的小孔隙束縛水,根據產水率劃分水淹級別,將束縛水電阻率輸入參數按照水驅油過程分為三個階段:未水淹階段,中低水淹階段,高水淹階段;
最后得出不同注入水礦化度下電性規律計算公式,即不同含水飽和度下不同水的電導率計算如下:
其中,假設在未水淹階段無離子交換;在中低水淹階段假設注入水離子與大孔隙薄膜束縛水逐漸交換,直到該階段結束完成,注入水與大孔隙薄膜束縛水完全離子交換;在高水淹階段,注入水開始與小孔隙束縛水進行離子交換,直到注入水將油完全驅替,束縛水礦化度等于注入水礦化度;
未水淹階段,產水率fw≤10%,大、小孔隙束縛水礦化度為地層原始礦化度;
中低水淹階段,產水率10%<fw≤80%,進行離子交換的束縛水電阻率:
其中,
高水淹階段,產水率fw>80%,進行離子交換的束縛水電阻率:
其中,
基于步驟b構建的水淹層數字巖心,將以上公式計算得到的參數、注入水礦化度參數等輸入電性計算中,得出不同注入水礦化度下電性規律;
d.構建水淹層新飽和度模型
根據步驟c所述,漸進混合式水淹層新飽和度模型分為三個階段:
第一階段,未水淹階段,地層產水率fw≤10%,混合液電阻率計算公式:
式中,rz為混合液電阻率,sw為地層中含水飽和度,swi為束縛水飽和度,rwi為束縛水電阻率,rwj為注入水電阻率;該階段的起始狀態為sw=swi,混合液電阻率為束縛水電阻率,沒有注入水注入,該階段的結束狀態為未水淹階段的結束,即sw=swt1,swt1為fw=10%時地層含水飽和度;
第二階段,中低水淹階段,地層產水率10%<fw≤80%,含水飽和度與注入倍數之間的關系如下式所示:
等效的注入水與大孔隙束縛水部分離子交換后的混合液礦化度為cwp:
混合液電阻率為:
式中,參數p計算方式與第三步計算方式一致,束縛水礦化度cwi,注入水礦化度cwj,t為溫度,單位為攝氏度;
混合液電阻率rz為:
第三階段,高水淹階段,地層產水率fw>80%。等效的注入水及大孔隙薄膜束縛水與小孔隙束縛水部分離子交換后的混合液礦化度cwq:
混合液電阻率為:
式中,參數q計算方式與第三步計算方式一致,束縛水礦化度cwi,注入水礦化度cwj,t為溫度,單位為攝氏度;
混合液電阻率rz為:
在得到混合液電阻率rz后,將其帶入印度尼西亞方程,從而計算水淹層含水飽和度:
式中,vclay為泥質含量,rt為地層電阻率。
所述水淹層數字巖心構建方法中的ct掃描方法是從水淹層取心后進行ct掃描,對ct掃描圖像進行濾波處理、圖像分割及代表元體積分析后得到巖石基質的三維數字巖心;數值模擬方法是根據常規巖心分析孔滲數據約束,采用過程法構建水淹層數字巖心。
本發明與現有技術相比較,具有以下優點:基于數字巖心的水淹層新飽和度模型計算水淹層飽和度,能夠考慮大孔隙薄膜束縛水和小孔隙束縛水離子交換作用,得到不同注入水礦化度下電性規律,可以準確計算水淹層飽和度,為測井評價儲層以及油田開發提供幫助,在計算水淹層飽和度方面具備其它滲透率模型無可比擬的優勢,實際應用效果顯著,因此極具推廣價值。
附圖說明
下面是結合附圖和實施例對本發明進一步說明。
圖1是新等效水淹層巖石體積物理模型示意圖;
圖2是水淹層數字巖心的示意圖;
圖3是水淹層數字巖心不同注入水礦化度下電阻率變化規律;
圖4和圖5是利用本發明對埕島油田井測井資料處理成果圖;
圖6是新飽和度模型計算結果與實驗分析結果進行對比圖。
具體實施方式
下面結合附圖和實施例來詳細說明本發明。
基于數字巖心的水淹層新飽和度模型的構建步驟如下:
第一步,建立新等效水淹層巖石體積物理模型。
如圖1所示為新等效水淹層巖石體積物理模型,包括五部分:巖石骨架、剩余油、大孔隙薄膜束縛水、小孔隙束縛水、孔隙中注入水。
第二步,構建水淹層數字巖心。
收集水淹層巖心粒度資料和壓汞資料,常規巖心分析孔隙度36.07%,滲透率1189.10md,根據孔、滲參數對沉積過程進行約束,采用過程法構建水淹層數字巖心,模型的分辨率為15μm,邊長為1.05cm,如圖2所示(孔隙1,骨架2)。由于模型尺寸較大,數值模擬計算量也較大,因此需要選擇一個大小合適的數字巖心,既具有相似的巖石物理屬性,又具有較高的運算效率。對數字巖心進行rev分析,選取的邊長為0.3mm較為合適。
第三步,數字巖心技術進行水淹機理分析,研究不同注入水礦化度下電性規律。
基于第二步rev分析后構建的數字巖心,采用格子boltzmann方法,得到數字巖心中流體流速分布,當孔隙中流體流速為零時,認為該部分孔隙為束縛水。束縛水位置不變,采用數學形態法確定孔隙內其它位置的流體分布,進而得到不同含水飽和度下巖心流體分布。該數字巖心束縛水飽和度為35.73%,殘余油飽和度22.01%,大孔隙薄膜束縛水飽和度30.28%,小孔隙束縛水飽和度5.45%。經過計算,未水淹階段結束fw=10%時地層含水飽和度為40.93%,中低水淹結束fw=80%時地層含水飽和度為49.35%。埕島油田原始地層水的礦化度平均為4730mg/l,因此,在數值模擬中采用地層水礦化度4730mg/l,注入水礦化度分別為1000mg/l,3000mg/l,8000mg/l,15000mg/l,30000mg/l。在20℃下,地層水電阻率1.25ω.m,注入水電阻率分別為5.46ω.m,1.92ω.m,0.76ω.m,0.42ω.m,0.23ω.m。在電性計算輸入參數時,油和骨架的電導率均為0,而孔隙中的水分為經過離子交換的注入水、大孔隙經過離子交換的束縛水、大孔隙原始束縛水、小孔隙經過離子交換的束縛水、小孔隙原始束縛水五類。
未水淹階段、中低水淹階段、高水淹階段不同含水飽和度下不同水的電導率計算如下:
未水淹階段,注入水量少,注入水接觸到束縛水體積少,產水率fw≤10%,大、小孔隙束縛水礦化度為地層原始礦化度;
中低水淹階段,注入水量增加,產水率10%<fw≤80%,注入水與大孔隙束縛水離子混合程度等效為注入水與大孔隙束縛水體積的p倍(0≤p≤1)中的離子完全平均混合,假設參數p是線性變化的,即參與注入水離子交換的大孔隙薄膜水的體積是線性增加的,直到該階段結束,所有大孔隙薄膜束縛水均與注入水離子完全平均混合,此時,地層產水率fw=80%,p的計算公式為:
參數p=0為中低水淹階段開始時,即sw=swt1,swt1為fw=10%時地層含水飽和度,p=1為中低水淹階段結束時,即sw=swt2,swt2為fw=80%時地層含水飽和度。進行離子交換的束縛水電阻率:
其中,
高水淹階段,產水率fw>80%,注入水開始與小孔隙束縛水進行離子交換,直到注入水將油完全驅替,束縛水礦化度等于注入水礦化度。注入水及大孔隙薄膜束縛水與小孔隙束縛水離子混合程度等效為注入水及大孔隙薄膜束縛水與小孔隙束縛水體積的q倍(0≤q≤1)中的離子完全平均混合,假設參數q是線性變化的,即參與注入水離子交換的小孔隙束縛水的體積是線性增加的,直到該階段結束,所有小孔隙薄膜束縛水均與注入水離子完全平均混合,q的計算公式為:
參數q=0為中高水淹階段開始時,即sw=swt2,swt2為fw=80%時地層含水飽和度;q=1為水淹階段結束時,即sw=1。進行離子交換的束縛水電阻率:
其中,
基于步驟b構建的水淹層數字巖心,將以上公式計算得到的參數、注入水礦化度參數等輸入電性計算中,得出不同注入水礦化度下電性規律。
在參數確定后,利用有限元方法計算不同注入水礦化度和不同含水飽和度條件下巖石電阻率。圖3為水淹層數字巖心cb1fb-3-20為不同注入水礦化度下電阻率變化規律,可以發現當注入水礦化度小于地層水礦化度,巖心電阻率隨著含水飽和度增加呈現先減小后增大再減小的“s”型曲線。礦化度越低,“s”曲線上升幅度越大。當注入水礦化度大于地層水礦化度,巖心電阻率隨著含水飽和度增加逐漸減小,礦化度越高,減小的幅度越大。
第四步,構建水淹層新飽和度模型
漸進混合式水淹層新飽和度模型分為三個階段。
第一階段,未水淹階段,地層產水率fw≤10%,混合液電阻率計算公式:
式中,rz為混合液電阻率,sw為地層中含水飽和度,swi為束縛水飽和度,rwi為束縛水電阻率,rwj為注入水電阻率。該階段的起始狀態為sw=swi,混合液電阻率為束縛水電阻率,沒有注入水注入,該階段的結束狀態為未水淹階段的結束,即sw=swt1,swt1為fw=10%時地層含水飽和度。
第二階段,中低水淹階段,地層產水率10%<fw≤80%,假設地層大孔隙薄膜束縛水swi1,小孔隙束縛水swi2,總束縛水swi,注入倍數為k,巖石體積v,孔隙度φ注入水驅替地層中油氣,地層此時含水飽和度為sw,累計注入量為kvφ,產油氣量qo=φv(sw-swi),產水量qw=kvφ-φv(sw-swi)=φv(k-(sw-swi))。
產水率公式:
含水飽和度與注入倍數之間的關系如下式所示:
等效的注入水與大孔隙束縛水部分離子交換后的混合液礦化度為cwp:
混合液電阻率rz為:
式中,參數p計算方式與第三步計算方式一致,束縛水礦化度cwi,注入水礦化度cwj,t為溫度,單位為攝氏度。
混合液電阻率rz為:
第三階段,高水淹階段,地層產水率fw>80%。等效的注入水及大孔隙薄膜束縛水與小孔隙束縛水部分離子交換后的混合液礦化度cwq:
混合液電阻率為:
式中,參數q計算方式與第三步計算方式一致,束縛水礦化度cwi,注入水礦化度cwj,t為溫度,單位為攝氏度。
混合液電阻率rz為:
在得到混合液電阻率rz后,將其帶入印度尼西亞方程,從而計算水淹層含水飽和度:
式中,vclay為泥質含量,rt為地層電阻率。
第五步,實際資料處理
收集井中20塊水淹層巖心資料,對于每塊巖心重復以上四步。通過對構建的20塊數字巖心進行分析,發現大孔隙薄膜水與
相關系數r2為0.70。
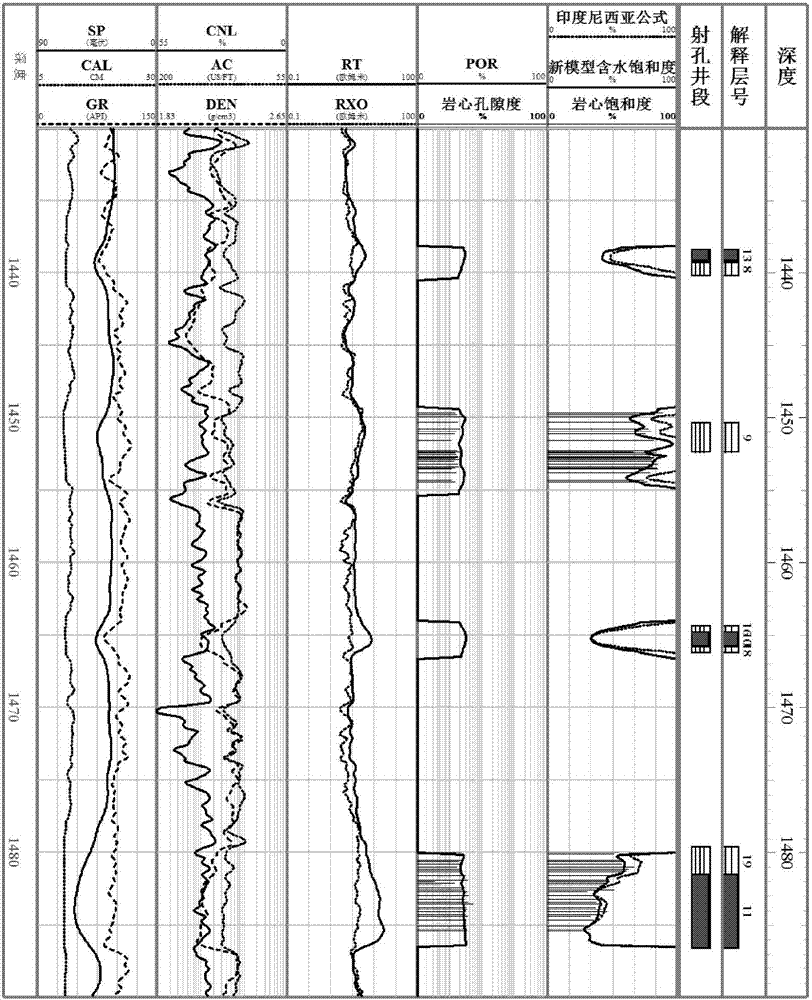
利用收集到的巖心分析資料擬合相滲透率經驗公式、總束縛水飽和度經驗公式、殘余油飽和度經驗公式,埕島油田地下原油粘度平均33mpa﹒s,原始地層水粘度0.446mpa﹒s。地溫梯度0.0385℃/m。將這些計算參數帶入水淹層新飽和度模型并編制處理程序。在實際計算過程中為減小誤差,采用迭代的方法求取地層含水飽和度。根據井密閉取芯對應的層位,利用編制的新水淹層測井飽和度解釋程序,選取兩個深度段進行處理,分別為1260m-1310m和1430m-1490m,處理結果如圖4和圖5所示。將新飽和度模型計算結果與實驗分析結果進行對比,如圖6所示,平均相對誤差為8.86%,驗證了基于數字巖心的水淹層新飽和度模型的適用性。
利用本發明基于數字巖心的水淹層新飽和度模型計算水淹層飽和度,能夠解決目前水淹層飽和度模型水淹機理與實際條件相差較大、飽和度計算精度較低的問題。基于數字巖心技術進行水淹機理分析,將束縛水分為大孔隙薄膜束縛水和小孔隙束縛水兩類并分別考慮離子交換,得到不同注入水礦化度下電性規律,可以獲得更加準確的測井解釋水淹層飽和度,為儲層評價提供有力幫助,具有較高推廣價值和社會效益。
本發明并不限于上述的實施方式,在本領域技術人員所具備的知識范圍內,還可以在不脫離本發明宗旨的前提下做出各種變化,變化后的內容仍屬于本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!