一種空天飛行器熱防護系統快速分析與設計方法與流程

技術領域：

本發明涉及空天飛行器熱防護系統分析與設計領域，特別涉及一種基于有限差分法的非穩態熱傳導分析和熱防護系統尺寸優化設計方法。

背景技術：
：

空天飛行器在服役環境中受嚴重的氣動加熱作用，表面氣動加熱產生的高溫，以及在結構內部引起的熱應力嚴重威脅結構安全。為應對結構高溫及熱應力作用，在空天飛行器結構設計中，需大量采用耐高溫的熱結構及熱防護系統(thermalprotectionsystem，tps)。tps由隔熱層、防熱層以及承力結構三部分構成。這些結構在飛機服役過程中受氣動力、氣動熱、慣性力、振動和噪聲等復雜載荷及環境綜合作用，要進行這類受熱結構的設計，常規飛機結構的設計方法已不能滿足要求，需要制定針對這類結構特點的結構設計頂層文件。

國內外針對tps的關鍵技術都做了大量的研究。國外從上世紀五、六十年代起，對氣動加熱的計算方法做了大量理論性研究，目前主要集中在使用熱防護的結構形式的工藝、材料和試驗的研究。martin等通過隱式一維有限元模型比較了10種不同的熱防護結構，在可重復使用飛行器再入過程中一系列氣動熱載荷下的比較分析，得出防熱氈式結構在絕大多數使用范圍內都有最輕的重量，陶瓷防熱瓦和金屬tps具有相近的重量。daryabeigi分析了熱力耦合分析的適用范圍，得出了耦合分析的重要性隨溫度的降低、載荷速率的增加和內部耗散的增加而增加。國內研究內容主要集中于氣動熱的計算、氣動外形設計和具體防熱結構的研究，很少有對新型空天飛行器方案的設計研究和新型的防熱結構構型設計。魏鑫、馬忠輝通過對幾種被動熱防護結構形式進行分析計算，給出了不同熱防護形式的防熱效果比較結果。在熱防護機理研究方面，閆長海提出了隔熱效率的概念，馬玉娥推導了熱力耦合的計算格式。由于流場與傳熱的模型計算量大，所以多數采用一維和二維模型，如尹凱軍對防熱瓦式熱防護系統的研究；趙玲對蓋板式熱防護結構的建模分析，李凰立、蘇大亮采用簡化的二維模型計算了熱流密度、溫度場和熱應力。實際的熱防護問題中，熱載荷除了向結構內部的傳遞外，由于飛行器不同部位熱載荷的巨大差異，橫向的熱載荷傳遞也十分重要。因此在復雜的熱載荷或主動冷卻條件下，三維的模型能夠更真實的反映熱載荷和機械載荷的傳遞和分布。對于熱防護系統的設計過程，三維分析十分必要。

然而，在空天飛行器設計概念設計階段需突出快速性要求，作為空天飛行器設計模塊中重要的一部分，快速分析設計也是熱防護系統設計需研究的重點。針對飛行器整機熱防護系統快速設計國內外學者開展了大量的研究工作。engel和praharaj采用經過驗證的工程方法計算飛行器表面特征點的熱流密度，結合這些特征點熱防護材料的一維溫度響應，實現了對熱防護系統的快速設計；并開發了相應的軟件平臺。為了滿足航天飛行器概念設計階段tps設計和分析能力mcguire、chen、bradford、coward等基于氣動力/氣動熱分析和熱防護系統設計/優化兩個模塊，發展了tpssizer、hyaat、sentry、tcat等熱防護系統自動設計工具。但上述方法存在不能實現熱防護系統方案選擇自動化、需要使用其他軟件進行分析等不足。國內目前主要是通過數值方法對特定tps進行分析設計，還沒有針對飛行器整機熱防護系統設計的成熟工具軟件和方法。

技術實現要素：
：

本發明的技術解決問題：綜合國內外研究現狀，本發明旨在對現有的熱防護系統分析與設計方法和理論進行綜合整理和對比研究，突出空天飛行器概念設計階段的快速性要求，形成適合空天飛行器快速熱防護系統分析和快速設計理論和方法。同時，發展和編制快速熱防護系統分析與設計程序一套，該程序能夠計算熱防護系統材料表面的瞬時深度熱傳導，以便在上升和再入階段保護飛行器；該程序也可以整合至空天飛行器總體設計的快速設計平臺內，提高整個概念設計過程的速度和自動化水平。

本發明的技術解決方案：一種空天飛行器熱防護系統快速分析與設計方法，其分析過程包括內外循環：其中，內循環為一維熱傳導分析計算過程，而外循環為優化設計過程。整個快速分析與設計方法包括四個模塊，即：一維非穩態熱傳導計算模塊、tps厚度優化模塊、tps結構內壁節點坐標確定及結構總重計算模塊以及tps分析與設計程序結構說明模塊。

一維非穩態熱傳導計算模塊：考慮飛行器表面傳熱機理，由有限差分格式求解。首先，飛行器表面傳熱機理如下。為方便描述，以光滑表面一維傳熱為例，在一個連續區域內其熱量傳遞情況如圖1所示：

(1)由能量守恒定律表面熱流之和為0，可得：

qgw+qrad，w，nc+qrad，g-qrad，w-qw＝0

表面溫度ts為熱量達到平衡時的溫度。此處假設tgw≡ts，忽略在滑流區域內可能存在的溫度跳躍。

(2)在高超聲速飛行中，熱量傳遞給飛行器表面主要通過三種物理過程實現：

①第一種是氣體往表面的熱量擴散，即表面處的熱流qgw。通常包括熱傳導，在熱化學非平衡條件下質量擴散所引起熱傳遞以及滑流產生的熱傳遞。

②第二種是由于非凸面效應，來自飛行器其它表面的熱輻射所傳遞的熱量qrad，w，nc。這種熱傳遞可以通過一個假定或等效的輻射系數εeff來進行描述。它考慮了所涉表面部分的相互可見性，尤其是特征邊界層的厚度，其局部決定了表面輻射熱流qrad，w。在分析中，來自太陽的輻射加熱忽略不計。

③第三種是激波邊界層內處于振動激發、離解和電力狀態下的氣體所產生的熱輻射qrad，g。對于傳統近地軌道再入飛行器，以及飛行速度v＜≈8km/s，飛行高度h＜≈100km的cav來說，由于氣體對流換熱qgw占主導地位，qrad，g通常可以忽略不計。

(3)飛行器表面通過兩種方式散熱：

①出于冷卻目的的表面輻射散熱qrad，w，本文中通常表示為qrad：

其中，ε為飛行器表面輻射系數；σ為stefan-boltzmann常數。

②表面材料的內部熱傳導qw，下文用qcond表示。這是一種自然的熱傳導過程，其主要取決于外層結構的厚度，即本發明所提的tps結構厚度。通常情況下，qcond遠小于qrad。但為了得到熱載荷的精確預測值，就必須考慮圖1所示完整的熱傳遞情況。本模塊將重點探討如何采用數值方法快速分析tps材料中的熱傳導過程。

考慮該飛行器熱防護系統快速分析與設計方法需滿足的快速性設計要求，本模塊選取一維熱傳導有限差分格式求解，一維非穩態熱傳導方程如下：

tps外邊界x＝0及內邊界x＝l邊界條件分別如下：

其中，由于氣體對流換熱qgw占主導地位，有qconv＝qgw。需要指出，x＝0邊界條件即為前文所述需滿足的能量守恒定律，包括流場的對流換熱qconv，表面高溫產生的熱輻射qrad＝εσts⁴以及tps材料熱傳導所吸收的熱量qcond＝-kdt/dx。而x＝l邊界處假設tps結構內邊界(機體表面)絕熱。

對上邊界，考慮到邊界條件(x＝0處)，使用向前差分法，可得：

其截斷誤差為o(δt，δx)。

對內部節點，采用中心差分法，可得：

對內邊界，考慮到邊界條件(x＝l處)，使用向后差分法，得下式：

建立上述所有節點的差分方程后，可以構造如下非線性方程組：

……

采用牛頓迭代法解上述方程組，第一步建立雅可比矩陣

將問題轉化成為如下公式所示的非線性方程組ax＝b求解。其中，a為雅可比矩陣，x為時間節點n+1處的溫度變化，且在時間節點n處，b＝-f。

通過估算節點n+1時的初始溫度，采用追趕法來計算每一個空間節點處的δtⁿ⁺¹，則下一步迭代計算時，節點n+1處的溫度變為tⁿ⁺¹＝tⁿ⁺¹+δtⁿ⁺¹。當向量δtⁿ⁺¹、向量fⁿ二范數的絕對值小于給定臨界值(如：1×10^-6)或是迭代達到給定的最大迭代次數(默認為1000次)時，迭代終止。這里，可假設第一時間節點n+1處材料的溫度迭代初值為1000k。

當需要分析多層材料熱防護結構時，在不同材料層(第i層與第i-1層)之間選取如下公式所示的邊界條件。

其中，ki為第i層對應的導熱系數。需要指出的是，假設層間動反作用存在(kineticreactions)，且層間滿足化學平衡而不滿足熱平衡。同時，假設各材料屬性在整個分析過程中保持常數，若需考慮材料屬性隨溫度變化的材料，可考慮采用線性或三次樣條曲線插值函數。

另外，可考慮結構內邊界也有表面熱流的一類邊界條件，此時，內邊界的表面熱流應和導熱熱流相等，如下公式所示，其中n表示內邊界上的點。

選用向后差分格式，整理后可得

tps厚度優化模塊將通過優化分析輸出結果為tps重量、厚度等參數。該優化問題的描述如下：

s.t.ti層外壁，max，(x)-ti，limit≤0，i＝1，2，...，m

ti層內壁，max(x)-ti，limit≤0，i＝1，2，...，m

其中，設計變量x＝(x1，x1，...，xm)為m層tps材料對應的材料厚度，第i(i＝1，2，...，n)個設計變量定義域為li≤xi≤ri；目標函數為tps結構總重量(質量)，可表示為tps表面參考點單位面積上各層厚度與材料密度的函數，ρ＝(ρ1，ρ2，...，ρm)為各層材料的密度；約束函數表示為傳導過程中各層上下表面節點處最大溫度ti層外壁，max(x)及ti層內壁max(x)均不超過材料極限許用溫度ti，limit。

采用nasa開發的conmin優化模塊(fortran語言編寫)進行優化分析，輸出目標函數值，優化迭代次數，最優設計變量等。具體分析過程將在后文中將詳細介紹。

tps結構內壁節點坐標及結構總重計算模塊：由tps厚度優化模塊得到tps結構表面各節點對應的厚度，便可以按結構劃分的單元、單元各節點坐標及對應厚度導出tps單元結構體的幾何關系，從而求得各單元結構體的體積、各單元節點對應內部節點的坐標、tps結構的總體積及總重，具體計算過程將在后文具體實施方式中展示。

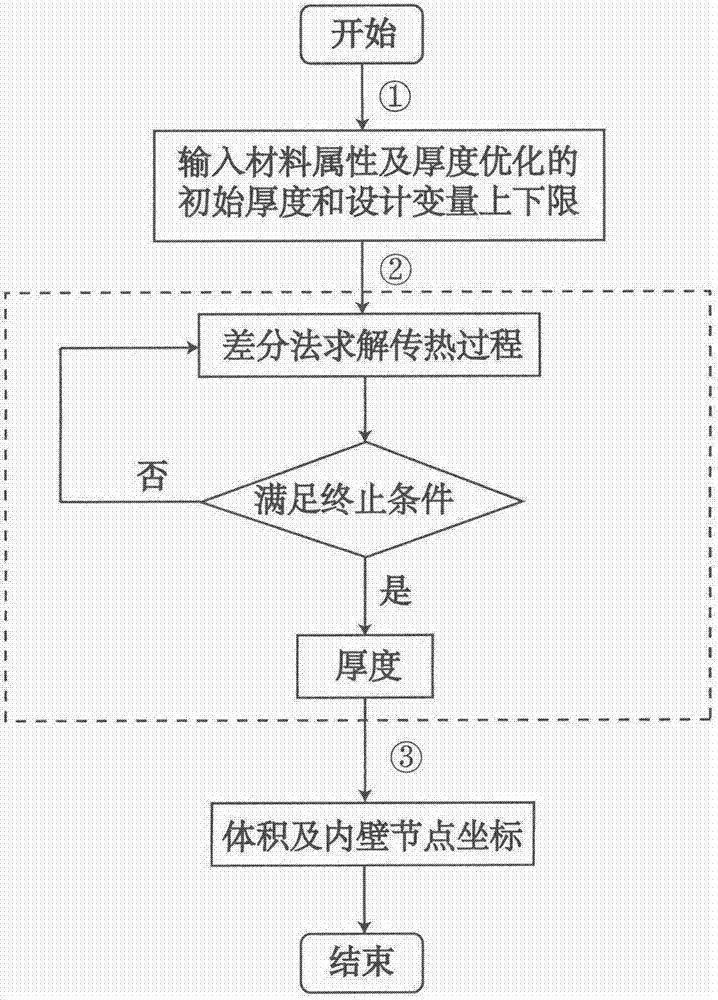
tps分析與設計程序結構說明模塊，其計算流程見圖3。其中，步驟①②需在給定txt格式輸入文件后運行tps厚度優化模塊程序，并由txt格式文件輸出各個節點對應的設計厚度值以及計算時間；步驟③需讀取步驟②的txt格式文件厚度計算結果及單元和相應節點信息，進而運行tps結構內壁節點坐標及結構總重計算模塊程序，由txt格式文件輸出各單元對應的單元體積、熱防護結構的總體積及總重以及結構內壁相應節點坐標。其中，步驟②有限差分格式熱傳導分析的tps模塊分別：差分法求解熱傳導方程的主程序，幫助讀取熱傳導分析所需的溫度、熱流及時間步長信息的子程序，采用追趕法求解分析過程出現的三對角矩陣的子程序以及計算有限差分法終止判據所需的第二類范數的外部函數。而步驟③也包括用于計算內壁相應節點坐標及各單元體積、熱防護結構總體積、總重兩個子程序。需要指出，用于計算內壁相應節點坐標的子程序可以處理任意結構體，而計算各單元體積、熱防護結構總體積、總重的子程序需要依據相應的幾何結構修改內部幾何關系設置，默認幾何結構為后文算例中的鈍頭椎體結構。

本發明與現有技術相比的優點在于：

(1)采用有限差分格式求解一維非穩態熱傳導問題，分析工具快速有效，突出了分析過程的快速性。

(2)采用以熱防護系統防熱材料厚度為目標函數、各層內材料許用溫度為約束函數的優化方法，可以給出熱防護系統厚度(尺寸)，提供了一種更優的熱防護系統設計方案，適用于工程應用。

(3)根據厚度優化結果確定內壁節點坐標以及采用單元結構體近似法求解單元結構體體積，可以有效完善熱防護系統快速設計方案。

(4)由于該系統各模塊之間相對獨立，每個模塊都有各自獨立的輸入、輸出文件，便于修改和維護。

附圖說明：

圖1連續區域內表面熱狀態示意圖；

圖2熱防護模塊計算流程圖；

圖3鈍頭錐體示意圖；

圖4各單元對應的防熱結構體示意圖；

圖5尖端球冒處內外節點幾何關系示意圖；

圖6后部椎體處內外節點幾何關系示意圖；

圖7鈍頭椎體結構內外壁節點多視圖。

具體實施方式：

下面結合附圖和實例對本發明做進一步說明。以一種典型15°半錐角鈍頭椎體結構的一維非穩態傳熱過程為實例。該結構選自nasa報告《effectsofangleofattackandbluntnessonlaminarheatingratedistributionsofa15°coneatamachnumberof10.6》，結構尺寸如圖3所示，結構尖端是半徑為0.0095m的球帽，后部整體為15°半錐角的椎體。

(1)節點處厚度計算

選取強化碳碳復合材料(rcc)(材料密度1580kg/m³，比熱0.77kj/kg-k，導熱系數k，4.3w/m-k，輻射系數，0.79)，默認壁面溫度為300k，材料許用溫度1900k(為便于案例應用，此處內壁許用溫度僅保守取到1450k，可作為今后設計時，內部第二層材料的參考許用溫度)。其中，外壁面邊界表面熱流密度數據qconv由氣動熱計算獲得，氣動熱計算過程選取對稱結構的一半(關于xoy平面對稱，取z正方向部分)，在結構表面共選取3708個節點、建立7192個三角形單元；本例的熱傳導分析過程也采用相同的處理方法，在對應節點處進行。結合實際條件，假設內壁絕熱，選取一維非穩態熱傳導計算模塊所述的x＝l邊界對應的邊界條件。

所有計算過程均由visualstudio編譯環境下的fortran90代碼編寫，采用intercore-i7(cpu@3.40ghzand8.0gbram)的臺式機進行計算。本例材料層數為1，考慮結構尺寸(鈍頭體尖端球帽半徑為0.0095m)，選取初始設計變量厚度為0.008m、設計變量定義域為[0.00635，0.009](m)；同時，取時間步長為1s，總時間2000s。在各節點處，采用tps厚度優化模塊進行外循環，一維非穩態熱傳計算模塊進行內循環，最終獲得各個節點對應所需熱防護材料厚度t。由于本例所選取的許用溫度約束較大且優化目標為線性形式，所有節點處的厚度在優化過程中均最終快速收斂為最優值0.00635m。

(2)防熱結構內部各節點位置及結構總重計算

將(1)中各節點對應的厚度數據讀入tps結構內壁節點坐標及結構總重計算模塊，可計算出防熱結構內部各節點位置、各單元對應的防熱結構體積及結構總重。具體計算過程如下：

(1)各單元對應的防熱結構體積及結構總重

各節點處，熱防護結構厚度方向為垂直外表面指向內部，如圖4所示。三角形單元各節點a、b、c由相應厚度ta、tb、tc對應內部節點a′、b′、c′。由于單元尺寸足夠小，可采用如下公式的近似方法，

v＝sabc×(ta+tb+tc)/3

取厚度ta、tb、tc的均值作為該結構的等效厚度，求得圖4所示的五面體結構體積，其中v為單元熱防護結構體積，sabc為三角形單元面積。再將各單元體積求和，可得該熱防護結構的總體積及總質量。本例中，鈍頭椎體熱防護結構的總體積為0.00179m³，總質量為2.821kg(如前文所述，實際計算只取一半對稱結構)。

(2)內部各節點位置

該鈍頭椎體結構分為尖端球帽和后部椎體兩部分，求內部各節點位置時將兩部分分開考慮。

①尖端球帽

在尖端球帽部分(x方向坐標0.03426m之內，見圖3)，外壁面節點a與由厚度對應的內部節點a′的幾何關系如圖5所示，a與a′在圖5所示的空間笛卡爾坐標系下對應的坐標分別為(xa，ya，za)及(xa.，ya.，za.)，(xa.，ya.，za.)可按如下公式求得：

cosβ＝(xoo-xa)/r

xa′＝xa+t×cosβ

za′＝(r-t)×sinβ×sinα

其中，xoo為球帽結構對應球心oo點的x軸坐標。

②后部椎體

在椎體部分(x方向坐標0.03426m～0.5687m，見圖3)，外壁面節點a與由厚度對應的內部節點a′的幾何關系如圖6所示，(xa.，ya.，za.)可按如下公式求得。

xa′＝xa+t×sin15°

za′＝(xa/cos15°/cos15°×sin15°-t)×cos15°×sinα

將所得內壁面節點數據和原始外壁面節點數據導入catia軟件，可生成該熱防護結構的整體結構關系圖，見圖7。其中，黑點表示外壁面節點，白點表示由上述計算得出的對應內壁面節點。

以上所述的僅為本發明的較佳實例，本發明不僅僅局限于上述實例，凡在本發明的精神和原則之內所做的局部改動、改進等均應包含在本發明的保護范圍之內。