一種高效解決堆芯燃料棒非穩態導熱問題的模擬方法與流程

本發明屬于核電廠溫度測量控制領域，特別涉及一種高效解決堆芯燃料棒非穩態導熱問題的模擬方法。

背景技術：

核電站堆芯燃料棒是反應堆中溫度最高的部分，因此為了避免堆芯熔毀，就需要時刻掌握燃料棒各個位置的溫度，通過控制堆芯反應性，使燃料棒溫度在合理范圍內。

為了獲取堆芯燃料棒的溫度，我們在需要的位置插入溫度探測器。但探測器的個數是十分有限的，并且為了避免溫度探測器損壞，溫度探測器大都被安置在堆芯燃料棒兩端，溫度較低的位置。這種通過溫度探測器得到的溫度參數雖然較為準確，但由于探測器個數、位置的限制導致所得的溫度參數是離散的幾個溫度點，并且由于探測器本身在測量溫度時具有一定的滯后性，因此單純的利用溫度探測器得到的燃料棒溫度分布情況局限性較大。正如切爾諾貝利核電站在1986年4月26日進行半烘烤實驗時發生事故，正是由于實驗人員不能掌握到堆芯燃料棒整體的溫度分布情況，并且由于反應性控制、溫度探測器的滯后性，以及沒有科學可靠的燃料棒上的溫度預測，因此使得實驗人員誤操作，造成了難以彌補的損失。

在此次事故之后，人們增加了對反應堆燃料棒溫度的監控，在加入了更多的溫度探測器后添加了數值模擬方法，因此可以得到燃料棒上整體的溫度分布情況，用于為調節堆芯反應性提供參考。現有方法時在得到探測器所測得的溫度數據后，利用有限體積法對燃料棒溫度分布進行模擬。

上述計算方法存在不足之處：

（1）單純的利用溫度探測器只能得到幾個離散的溫度點，并不能得到燃料棒上整體的溫度分布；

（2）有限體積法在溫度場求解上具有較好的應用，但其采用區域離散的方法未知量涉及到全域,因此所建立的矩陣較大,所需計算時間較長，計算效率不高。

技術實現要素：

本發明針對現有技術的不足，提供了一種高效解決堆芯燃料棒非穩態導熱問題的模擬方法，本方法占用資源小，計算快速，結果可靠，尤其適用于在燃料棒功率發生波動的時候。

本發明采用的技術方案為：

步驟1，對實際燃料棒模型進行合理簡化，建立幾何模型，并對模型進行離散編號：

將總長為L的燃料棒平均（或不均勻）分成長度為 的n端，從上到下編號依次為：1、2、3…n、（n+1）

步驟2，采用降階的方法使原有的導熱二階偏微分方程變成了兩個一階偏微分方程組：

由非穩態能量守恒方程的偏微分方程得：

式中T為溫度，t為時間，為材料密度，c為材料比熱容，S為內熱源。

設 ，則V是溫度T在x方向上的溫度梯度于是有：

步驟3，建立數學模型上任意一點的各物理量關于初始點物理量的關系式；

通過積分化簡步驟2中的偏微分方程組，首先得到穩態情況下，燃料棒上任意一點i的溫度場與初始點1的溫度場之間的關系：

其中為第i點t時刻的溫度，為第i點t時刻的熱流量，為初始點t時刻的溫度，為初始點t時刻的熱流量

其中：

其中：

步驟4，利用已知邊界條件求解關系式中的未知量：

通過探測器做探測到的溫度作為已知，可以求解步驟3中所涉及到的未知量。

步驟5，求解所需位置在不同時刻的溫度參數；

如果燃料棒功率發生變化，則以變化的功率和穩態時的溫度參數作為已知，利用步驟4中得到的未知數，帶入步驟3中的關系式，求解出在接下來的時間內，燃料棒上的溫度分布。用于預測堆芯反應性調節對堆芯安全性造成的影響，避免燃料棒溫度過高;

而本文所采取的數值模擬方法就可以避免了超大型矩陣的建立和計算，在整個計算過程中，最高階矩陣只有兩階，并且矩陣大小不會隨模型節點數的不同而發生變化。這種只有小型矩陣參與計算的過程增加了計算機的計算速率，尤其在離散單元數量較多時，可以避免求解超大型矩陣，從而達到快速計算的效果。除此之外，使用本發明所使用的儲存空間較小，采用全局求解方法，溫度分布和熱流分布同時求解得到，無需再此求解;

也正是由于使用本方法可以高效、快速、準確的計算燃料棒的穩態，非穩態的溫度分布問題，因此也就可以更加快速的預測到控制棒發生變化時，燃料棒上溫度將要發生的變化，預測出是否會產生危險，保證了核電廠的安全運行。

附圖說明

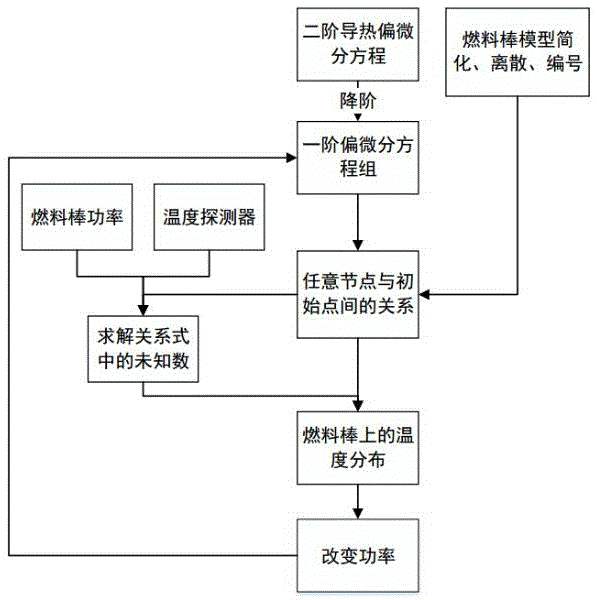
圖1為本發明方法流程圖；

圖2為簡化后的燃料棒示意圖；

圖3為穩態時燃料棒溫度分布的示意圖；

圖4為功率突然升高后燃料棒溫度隨時間變化的示意圖。

具體實施方式

本發明提供一種高效解決堆芯燃料棒非穩態導熱問題的模擬方法，下面結合附圖和具體實施方式對本發明做進一步說明。

根據如圖1所示的本方法的流程圖，對如圖2所示的燃料棒進行穩態、非穩態分析，以保證燃料棒安全工作。

對實際燃料棒模型進行合理簡化，建立幾何模型，并對模型進行離散編號，如圖2所示燃料棒為一個長直柱狀結構，內部包含有燃料芯塊，外部為冷卻劑。因此將燃料棒簡化為一個在軸向上的一維結構，燃料棒與冷卻劑換熱和燃料芯塊產熱部分被簡化為一個熱源加載在燃料棒上。

簡化后的燃料棒長L=3 m，截面積為A=7e-5 m2，沿軸向將其分成60，份共61個節點。通過堆芯內部的溫度探測器得到燃料棒兩端溫度分別為T_A=1100K ，T_B=1000K ，導熱率為25 W/(mK)，比熱容C=480J/(kgK) ，密度=8055Kg/m³ 。通過計算堆芯反應性得到沿軸向從下到上的燃料棒功率密度，與燃料棒和冷卻劑換熱進行疊加，作為一個熱源加載到燃料棒上，熱源項為：

對原有二階穩態導熱方程進行降階，并得到燃料棒上任意一點與初始點的關系。帶入上述已知條件，可以得到如圖3所示的計算結果，并利用有限體積法進行計算用以對新方法的準確性進行說明。

從圖3中可以看出，利用本發明對燃料棒穩態時的溫度分布進行分析與解析解分析結果吻合的非常好，利用本發明可以達到現有常規方法的計算精度，可以應用到工程應用當中去，并且，由于計算過程中，本發明只涉及到二階矩陣的計算，并不像有限體積法需要解一個60階的大矩陣，因此計算較為高效。除此以外，如果利用傳統的解析法進行求解，雖然結果精準，但是傳統解析法并不通用，如界面發生變化、模型材料參數發生變化等，傳統的解析法都不能很好的解決。

接下來調節控制棒和反應堆冷卻劑中的硼濃度，使得燃料棒的功率發生變化，使得燃料棒上的熱源從原有的，提升到， 則在接下來的時間里，燃料棒會由于其內部的功率變大，因此溫度場會隨時間發生變化并漸漸區域穩定。

如圖4所示，在燃料棒功率增高之后，燃料棒溫度隨時間而增大，在t=2 S與第10 S的結果誤差在2%以內，基本趨于穩定，燃料棒溫度逐漸趨于穩定，在x=1.45 m溫度達到最高，從最初的1657.3 K提升到了1814.6 K。