結合關鍵工序的遺傳局部搜索算法求解柔性作業車間調度的制作方法

本發明涉及作業車間調度技術領域，具體地涉及一種實用性強的柔性作業車間調度領域。

背景技術：

作業車間調度問題(Job Shop Scheduling Problem，JSP)作為典型的組合優化問題之一，其研究起始于20世紀50年代，最早要追溯到1954年科學家對兩臺機床的流水車間調度問題的提出和解決。近幾十年來，由于實際生產的需要和相關技術尤其是智能優化算法的不斷提出，越來越多的學者致力于JSP研究。從單資源約束到多資源約束、確定性到不確定性、單目標到多目標、小規模到大規模，各類JSP都得到了廣泛的研究。且已有部分智能調度方法的研究成果成功應用于實際生產過程中。

柔性作業車間調度問題(Flexible Job Shop Scheduling Problem，FJSP)更接近生產實際，是經典作業車間調度問題的延伸，最早是在1990年提出的，它的可行解范圍更大、問題的復雜性更高，因此屬于強NP-hard問題。FJSP是指建立FJSP的模型，通過某種算法為每項作業的每道工序分配適當的機器，并確定各機器上工序的加工順序，以在滿足各種約束條件的前提下，實現作業的完工時間最短、拖期最小、各機器的負載均衡等優化目標。

從FJSP的提出到現在，國內外有很多專家學者提出了多種算法。主要集中在改進粒子群算法、改進遺傳算法、混合算法等進化算法。遺傳算法(Genetic Algorithm,GA)作為一種啟發性搜索方法，是基于“適者生存”機制設計的算法，其思想來源于達爾文的進化論和孟德爾的遺傳學說。GA主要是通過從改進交叉操作和變異操作的角度以適應于具體問題的求解。但GA在進化過程中遺傳算子操作會出現不可行的解，且對于不同規模的柔性作業車間調度問題，其種群大小、變異率、交叉率等參數的不同選擇對求解的結果影響很大，使得求解結果不穩定，即使采用相同的參數進行求解，由于算法搜索過程中的隨機性，使得多次求解結果也存在不同程度的偏差，且存在局部搜索能力不足的問題。

技術實現要素：

針對上述的不足之處，本發明要解決的問題是提供一種結合關鍵工序的遺傳局部搜索算法，以控制局部搜索范圍，更快的找到可行解。

本發明的目標是：第一.解決進化過程中遺傳算子操作出現不可行解的問題；第二.遺傳搜索隨機性大，造成求解結果不穩定的問題；第三.計算時間長的問題。

本發明針對上述目的所采用的技術方案是：第一.對工序向量交叉操作后執行修復程序；第二.由于遺傳搜索提供較好的多樣性個體，局部搜索能探索最優方案，將兩者結合起來；第三.根據關鍵工序的移動才能影響總完工時間的概念，采用關鍵工序控制局部搜索范圍；第四.設計兩個向量分別代表工序順序和設備分配兩個子問題的編碼方式；第五.查找設備閑置時間的新的解碼方式。

該發明采用結合關鍵工序的遺傳局部搜索算法求解柔性作業車間調度，具體流程如下：

步驟1：采用隨機方式產生N個染色體作為初始種群，N為種群規模；

步驟2：判斷是否達到最大進化代數，是則返回最優解程序結束執行步驟10；否則執行下一步驟3；

步驟3：采用錦標賽選擇法選擇N×P_c個個體，P_c為交叉概率；

步驟4：將選擇的個體的染色體進行有修復程序的成對交叉；

步驟5：以變異概率P_m對交叉后的染色體進行變異操作；

步驟6：更新交叉變異后的種群N；

步驟7：采用錦標賽選擇法選擇N×P₁個個體，P₁為關鍵工序鄰域搜索概率；

步驟8：對選擇的個體基于關鍵工序的進行鄰域搜索；

步驟9：更新局部搜索后的種群N,進化代數加1，返回步驟2，重復操作；

步驟10：解碼染色體，返回種群N中C_max最小的方案，結束

本發明的有益效果是：第一.修復程序保證了遺傳操作后的染色體都是可行解；第二.遺傳算法與局部搜索結合能獲得總完工時間更小的調度方案；第三.限制關鍵工序的鄰域搜索，控制了搜索的方向，避免了不必要的搜索的范圍，大幅減少了計算時間；第四.新的編碼方式便于遺傳操作和理解；第五.新的解碼方式獲得的調度方案是最優的自動調度方案。

附圖說明

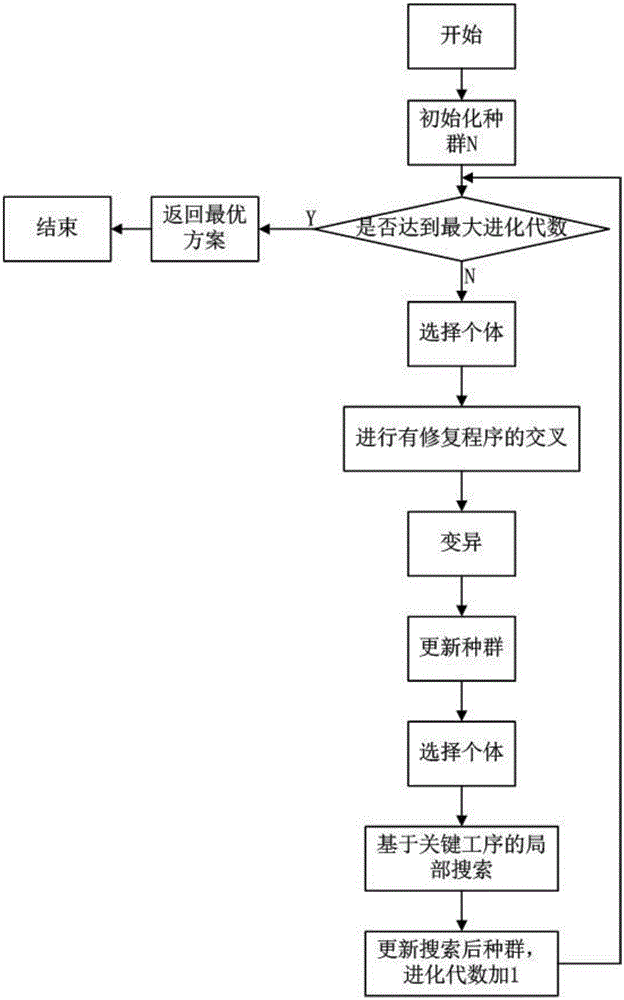
圖1表示本算法的詳細流程圖

圖2表示一個3個工件3臺設備的柔性作業車間問題實例。

圖3表示本算法所提出的改進的交叉算法過程實例，包括一個基因修復過程。

圖4表示本算法的解碼過程實例，這種解碼方式所獲得的調度方案是自動調度，是最優的調度方案。

圖5表示一個染色體解碼后所對應的析取圖，為了清除表示關鍵路徑和關鍵工序。

具體實施方式

為了使本發明的目的、技術方案及優點更加清楚明白，以下結合附圖和實施例對本發明進一步詳細說明。應當理解此處所描述的具體實施例僅僅用于解釋本發明并不用于限定本發明。基于本發明中的實施例，本領域技術人員在沒有作出創造性勞動前提下所獲得的所有其他實施例，都屬于本發明保護的范圍。

本發明針對現有的遺傳算法在進化過程中遺傳算子操作會出現不可行的解，且對于不同規模的柔性作業車間調度問題，其種群大小、變異率、交叉率等參數的不同選擇對求解的結果影響很大，使得求解結果不穩定，即使采用相同的參數進行求解，由于算法搜索過程中的隨機性，使得多次求解結果也存在不同程度的偏差，且存在局部搜索能力不足的問題。本發明提出了一種新的編碼、解碼方式，有修復程序的交叉操作，并且使用了基于關鍵工序的領域搜索方式，大大提高了算法的性能，能夠更好的運用到實際生產中。

多目標柔性作業車間調度問題可以結合圖2一個3個工件3臺設備的柔性作業車間調度問題實例表述，圖中“-”表示該設備不能加工到該工序。表述如下：n個獨立工件的集合J＝{J₁，J₂，…，J_n}，m臺設備的集合M＝{M₁，M₂，…，M_m}，工件J_i由n_i個優先約束的工序序列組成，這些工序根據給定的序列一個接一個的加工。每一道工序O_i，j表示工件J_i的第j道工序，必須從給定的一個子集M_i，j∈M中選擇一臺設備加工。工序的加工時間由設備決定。P_i，j，k表示O_i，j在設備M_k上的加工時間。調度安排包括兩個子問題:分配每一道工序一個合適的設備的路徑子問題和確定所有設備上的工序序列的排序子問題。

令C_i表示工件J_i的完工時間，優化目標是最小化總完工時間：

C_max＝max{C_i|i＝1，2，…，n} (1)

為了簡化問題，做了如下假設：所有設備在t＝0時刻都是可用的，所有工件在t＝0時刻釋放，每一臺設備在同一時刻只能加工一道工序，一道工序一旦開始加工不允許中斷，每一個工件的工序順序是預定的不能修改，忽略設備的設置時間和工序之間的轉換時間。

結合附圖和柔性作業車間調度問題模型，該算法的詳細流程表示如下：

步驟1：采用隨機方式產生N個染色體作為初始種群，N為種群規模；

柔性作業車間調度問題的解可以描述為工序到設備分配和工序在設備上的加工順序。因此，本算法的編碼方式采用由兩個向量組成的染色體決定，即設備分配向量和工序順序向量，很好的對應了柔性作業車間調度問題的兩個子問題，且便于交叉和變異操作。

首先，連續給每一道工序一個固定編號，以j的形式，j＝1,2，。。，d，即工序1到n₁屬于工件1，n₁+1到n₁+n₂屬于工件2，以此類推。比如圖2中O_3，1用新的編號工序6表示。

設備分配向量u＝[u₁，u₂，…，u_d]，1≤u_j≤l_j，j＝1,2，。。，d，如圖2所示的可行設備分配向量為u＝[1，1，1，1，1，1，1]，對應設備編號為u＝[M₁，M₂，M₂，M₁，M₃，M₂，M₁]。l_j表示對工序j可選擇的設備集合，為了方便統一表述，工序j的可選設備排序，按照他們加工工序j所需的時間升序排序。如果兩臺設備需要的時間相同，編號小的設備排在前面。然后u_j表示表示工件j選擇它的可選擇設備里的第u_j臺設備。

工序順序向量v＝[v₁，v₂，…，v_d]，是所有工序的編號置換，向量v中每一道工序出現的順序表示它的調度優先級如圖2所示問題的一個可行工序順序向量可表示為v＝[6，1，7，3，4，2，5].轉換為一個唯一的工序順序：O_3，1→O_1，1→O_3，2→O_2，1→O_2，2→O_1，2→O_2，3.工序O_3，1有最高的優先級，最先調度。

步驟2：判定是否達到最大進化代數，是則返回最優解程序結束執行步驟10；否則執行下一步驟3；

步驟3：采用錦標賽選擇法選擇N×P_c個個體，P_c為交叉概率；

步驟4：將選擇的個體的染色體進行有修復程序的成對交叉，圖3闡釋了關于圖2所示問題的改進的交叉過程：

所述交叉過程如下：交叉算子分別對一對染色體的兩個向量分別實施。對設備分配向量u，隨機選擇一個位置，然后通過交換兩個父代中所選擇的位置的值產生子代的設備分配向量u。對工序順序向量v，使用一種改進的順序交叉。描述如下：首先，隨機選擇兩點，選擇第一個父代中這兩點之間的工序；然后，復制這些工序到第一個子代中的相同位置；最后，用剩余的工序完成這個子代，以他們在第二個父代中的順序。但是，所獲得的工序順序可能是不可行的，由于一個工件的工序之間的約束。所以，執行一個簡單的修復程序，以調整相同工件的工序之間的相對順序。對第二個父代和子代重復對稱的過程。

所述交叉修復程序如下：

步驟4.1：賦值：[q₁，q₂，…，q_n]←[0，0，…，0]；

步驟4.2：如果迭代次數i＝1到d，執行下一步驟4.3；否則執行步驟4.7結束此程序

步驟4.3：找到工序v_i所屬的工件J_k

步驟4.4：q_k←q_k+1

步驟4.5：獲得工序O_k，q_k的固定編號op

步驟4.6：v_i←op

步驟4.7：結束

其中q_k表示工序，O_k表示第K個工件的第q_k道工序。

步驟5：以變異概率P_m對交叉后的染色體進行變異操作；

對交叉操作得到的子代個體循環每一個基因位，以變異概率p_m對該位基因進行變異操作。

步驟6：更新交叉變異后的種群N

步驟7：:錦標賽選擇法選擇N×P₁個個體，P₁為關鍵工序鄰域搜索概率。

本算法采用的染色體解碼方式結合圖4的甘特圖可以描述如下：根據工序排序向量v中順序一個接一個為每一道工序在其分到的設備上分配一段時間。當考慮一道工序時，首先從設備分配向量u中得到它所選擇的設備，然后從左往右掃描那臺設備上已經調度的工序之間的閑置時間區間，直到發現一個可用的區間。令s_i，j表示方案中的一道工序O_i，j的開始加工時間，c_i，j是它的完工時間。因為一道工序只能在它所屬工件的前一道加工工序完成之后才能開始加工，，當

設備M_k上的閑置時間區間[S_x，E_x]對O_i，j可用。當O_i，j被分配到可用區間[S_x，E_x]，max{S_x，c_i，j-1}(j≥2)或者S_x(j＝1)將視為該工序開始加工的時間。如果設備M_k上沒有適合O_i，j這樣的區間存在，他將被分配到設備的最后。

通過這種解碼方式產生的調度方案能夠保證是一個主動調度。比如圖2所示問題的一個染色體為u＝[1，1，1，1，1，2，1]，v＝[6，1，7，3，4，2，5]，解碼是一個實際調度表示為圖4的甘特圖。

所述主動調度是在半主動調度(指各工序按最早可能開始加工的時間進行加工的調度類型)基礎上的是指：任何一臺機器的每一段空閑時間都不足以加工一道可加工工序的半主動調度，一個半主動調度中將各工序在滿足工序前后順序約束的前提下盡可能向左移,就得到一個主動調度.很顯然,最優調度就是主動調度。

為了找到關鍵路徑上的關鍵工序，我們設計了一個析取圖，方便描述。

假設析取圖由G＝{V，C，D}表示，V表示點集，每一個點(包括開始和結束的點)表示一道工序；C表示合取弧集合，每一條合取弧對應相同工件的優先約束；D表示析取弧，每一條析取弧對應同一臺設備上加工的工序優先級。每一道工序所選擇的設備在點上標記，對應加工時間標記在點下，視為點的權重。開始和結束點權重為0.如果析取弧是無環的，表示對應柔性作業車間調度問題的一個可行解。并且從開始點到結束點之間最長的路徑叫做關鍵路徑，它的長度表示總完工時間。關鍵路徑上的任何一個工序叫做關鍵工序。在隨后的表述中，我們不區分工序和點，調度和析取弧。

以圖2所給的柔性作業車間調度問題實例，一個可行的調度析取圖描繪如圖5。在這個析取圖中，存在兩個關鍵路徑S→O_2，1→O_2，2→O_2，3→E和S→O_3，1→O_2，3→E，路徑長度都等于5。所以這個調度方案的總完工時間為5。O_2，1、O_2，2、O_2，3、O_3，1是所有的關鍵工序。

為了方便描述算法，基于析取圖G定義一些符號。u(G，v)表示析取圖G中一個節點v的選擇設備編號。令ES(G，v)表示節點最早開工時間，LS(G，v，T)表示節點在沒有延遲要求的總完工時間的最晚開工時間。對應地，最早和最晚完工時間分別表示為EC(G，v)＝ES(G，v)+p_v，u(G，v)和LC(G，v)＝LS(G，v)+p_u(G，v)。PM(G，v)表示在相同設備上v的前一道工序，SM(G，v)表示同一設備上v的后一道工序。令PJ(v)表示v所屬工件的前一道工序，SJ(v)表示v所屬工件的后一道工序。令nc(G)表示析取圖G中的關鍵工序數量，X(G)＝{co₁，co₂，…，co_nc(g)}表示關鍵工序的集合。

當且僅當ES(G，v)＝LS(G，v，G_max(G)),工序v是一個關鍵工序。如圖4的析取圖，O_2，2是一個關鍵工序，所以ES(G，O_2，2)＝LS(G，O_2，2，5)＝2，O_1，2不是關鍵工序，ES(G，O_1，2)＝2，LS(G，O_1，2，5)＝3；如果要求的總完工時間為6，LS(G，O_1，2，5)＝4。

步驟8：對選擇的個體基于關鍵工序的進行鄰域搜索

經證明，只有移動關鍵路徑上的工序，才會影響總完工時間。假設移動關鍵工序co_i，首先從調度方案G中刪掉它得到去掉指向co_i和從co_i引出的析取弧，用一條析取弧連接PM(G，co_i)和PM(G，co_i)，令點co_i的加權值為0.然后，co_i插入中另外一個可行的位置獲得G’使得C_max(G′)≤C_max(G)。如果這樣的一個位置在設備M_k上的工序v之前，co_i應該在開始加工，能夠在完工。另外，co_i必須滿足同一工件的工序約束。因此，應該滿足下面的不等式：

然而，在式(3)條件下插入co_i到v之前有時不能保證所得的G’是無環的。因此，將設備M_k上將被測試這些位置限制為可行的位置。令θ_l表示中設備M_k上加工的工序集合，以最早開工時間升序排序。(注意)。符號和ψ_k表示θ_k的兩個子序列，定義如下：

令R_k表示所有工序之前的位置與ψ_k所有工序之后的位置和ψ_k所有工序之前與所有工序之后的位置。插入co_i到設備M_k上獲得最優的方案的位置在集合R_k中。

因此，當重新給co_i在中設備M_k上分配一個位置時，只有γ_k中的位置會被檢查，一旦發現一個位置滿足式(3)，co_i立刻插入該位置，形成一個可接受的鄰域方案G’替換當前方案G。

對一個染色體基于關鍵工序的局部搜索程序描述如下：

步驟8.1：迭代次數等于0

步驟8.2:對所選擇的染色體個體(u，v)解碼，獲得調度方案G

步驟8.3：G復制給最優調度方案Gbest

步驟8.4：當G不為空，且未達到最大迭代次數，執行步驟8.5，否則執行

步驟8.15返回最優方案

步驟8.5：獲取G的關鍵工序集合X(G)＝{co₁，co₂，…，co_nc}

步驟8.6：對i＝1到nc，執行步驟8.7，否則執行步驟8.13

步驟8.7：將co_i從G中刪除得到

步驟8.8：根據式(4)、(5)獲取co_i對應的設備M_k上的可用位置R_k

步驟8.9：對于R_k的每一個位置r

步驟8.10：如果位置r滿足式(3)

步驟8.11：將co_i插入的該位置r得到G’

步驟8.12：用G’替換G,返回步驟8.6

步驟8.13：C_max(G)＜C_max(Gbest)，替換Gbest，否則保留Gbest

步驟8.14：迭代次數加1，返回步驟8.4

步驟8.15：Gbest編碼，以染色體形式返回最優方案

步驟9：更新局部搜索后的種群N,進化代數加1，返回步驟2

步驟10：解碼染色體，返回種群N中C_max最小的方案，結束。