針對多目標流水車間調度的加權式遺傳局部搜索算法的制作方法

本發明型專利用于制訂多目標流水車間調度的生產調度計劃。

背景技術：

遺傳算法是一種高效的全局搜索算法，其與局部搜索算法的結合，即遺傳局部搜索算法，使得算法對于非支配解的搜索能力大大提高。目前，這種全局搜索與局部搜索相結合的算法已經被廣泛地運用于生產優化之中，并取得了很好的效果。然而，現有的局部搜索算法往往難以簡單高效地找到多目標問題的全部非支配解。

技術實現要素：

本算法針對傳統的遺傳局部搜索算法作出改進，以簡單高效地找到多目標流水車間調度問題的全部非支配解。本算法對傳統遺傳局部搜索在以下三個方面進行改進：第一，每個目標函數的加權值不易確定；第二，對局部搜索過程中產生的大量鄰域解的比較往往占據大量的計算時間；第三，局部搜索方向不夠全面；第四，搜索過程中得到的優良解可能在之后的算法迭代過程中被遺失。

本發明型解決其技術問題所采用的技術方案是：第一，通過隨機加權法為每個目標函數賦予加權值；第二，限制局部搜索過程中對每個當前解搜索的鄰域解的個數；第三，以產生子代解的父代解所使用的加權值作為子代解在局部搜索中的目標函數加權值；第四，采用精英策略，將每一代中的非支配解存入暫時組并逐代更新。

本發明型的有益效果：第一，使確定目標函數加權值的過程不再困難；第二，平衡了全局搜索與局部搜索；第三，局部搜索中的每個解都有自己獨特的搜索方向，使得局部搜索的方向多樣化；第四，避免了產生的優良解在之后算法的迭代過程中被遺失。

附圖說明

下面結合附圖和實施例對本發明型進一步說明。

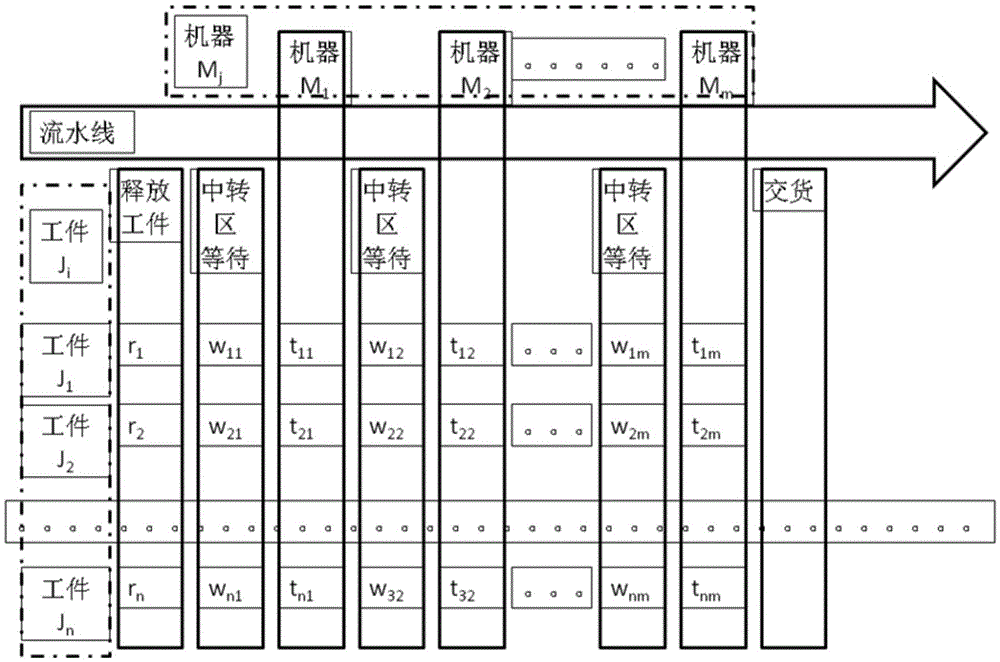
圖1是流水車間調度的示意圖。

圖2是局部搜索方向的示意圖。

圖3是非支配解的示意圖。

圖4是精英策略的示意圖。

圖5是加權式遺傳局部搜索流程的示意圖。

圖6是兩點交叉算子示意圖。

圖7是移動突變示意圖。

圖8是算法詳細流程的示意圖

具體實施方式

一、生產信息的表示

如圖1，設在流水車間中，有n個待生產的工件J₁，J₂，…，J_n，有m臺機器M₁，M₂，…，M_m，工件J_i的釋放時間為r_i，工件J_i的在機器M_j前的等待時間為w_ij，工件J_i的交貨時間：d_i。

二、調度方案的表示方法：

機器i上的調度方案表示為X_i＝(s₁，s₂，…，s_n)，1≤i≤m(s_i表示工件編號，1≤i≤n)，則總調度方案表示為X＝(X₁，X₂，…，X_m)

三、隨機加權法

對n個目標的加權值的賦值方法：

1.隨機產生n個和為1的加權值random₁，random₂，…，random_n；

2.第i個目標函數的加權值w_i為

w_i＝random_i/(random₁+…random_n)，i＝1，2，…，n.

四、只檢測部分鄰域解的局部搜索算法

指定鄰域解檢測個數k，將產生當前解X的父代解的目標函數加權值作為當前解X的目標函數加權值(這將使每個當前解都有自己獨特的局部搜索方向，從而使局部搜索方向多樣化，其特點被圖2形象地描述出來)，局部搜索采用移動突變的方式產生鄰域解。

那么，對于解X的局部搜索過程如下：

1.檢測當前解X的一個鄰域解X’；

2.如果X’是比X更優的解，則用X’替代當前解X并返回1；否則執行下一步；

3.如果當前解X的隨機選擇的k個鄰域解已經被檢測，即X的被檢測的k個鄰域解中沒有更優的解，則程序結束；否則返回1。

五、非支配解

對于最大化n個目標函數f₁(x)，f₂(x)，…，f_n(x)，當兩個解x、y滿

足

且

f_j(x)<f_j(y)時，則稱解y支配解x。如果一個解不被多目標優化問題的任何其他解支配，那個解被稱為一個非支配解。對于兩目標優化問題(最大化目標函數)的非支配解可以被圖3形象地描述出來。

六、精英策略

如圖4，本算法的執行過程中含有兩組解，分別為當前種群和存儲非支配解的暫時組。

每一代種群首先用本種群中的非支配解更新暫時組，并隨機選擇指定個數的解；然后，該種群經遺傳算子處理后，將之前隨機選擇的非支配解加入當前種群，共同進行局部搜索；局部搜索結束后產生的種群作為下一代繼續執行上述過程。七、加權式遺傳局部搜索

如圖5，本算法在初始化種群后，首先確定目標函數加權值，接著通過遺傳算子對種群進行全局搜索，然后進行局部搜索，而后采用精英策略保護非支配解，最后通過對上述過程的反復迭代來尋找全部的非支配解。

八、兩點交叉算子

如圖6

九、移動突變

如圖7

十、算法詳細流程如下

如圖8

步驟一——初始化(產生初始解)

1.產生m個序列(m為機器數)，每個序列為數1-n的一個隨機排序序列(n為待生產工件數)。

2.根據種群規模N_pop，產生對應數目的初始解。

步驟二——計算目標函數值

1.計算目標函數f₁(x)，f₂(x)，…，f_n(x)的值。

步驟三——更新暫時組的非支配解

1.尋找初始種群中的非支配解。

2.將初始解中的非支配解復制入暫時組。

步驟四——計算適應度函數值

對每個解——

1.確定加權值

w_i＝random_i/(random₁+…random_n)，i＝1，2，…，n.

2.計算適應度函數值：

f(x)＝w₁f₁(x)+w₂f₂(x)+…+w_nf_n(x).

步驟五——選擇優良個體

1.計算每個個體(解)的選擇概率

其中Ψ表示當前種群，f(x)為解x的適應度值，f_min(Ψ)＝min{f(x)|x∈Ψ}。

2.根據選擇概率，選擇選擇概率大的(N_pop-N_elite)個個體(解)。

步驟六——交叉

1.根據交叉概率計算進行交叉的解的數目，隨即選出相應個數的解。

2.隨機將被選擇的個體兩兩一組作為一對父代解，運用兩點交叉算子進行交叉。對每對父代解交叉時，分別對兩個解的每行進行交叉，再把結果重新組合成子代解。

步驟七——突變

1.根據突變概率計算進行交叉的解的數目，隨即選出相應個數的解。

2.對被選擇的個體進行移動突變。對每對父代解進行突變時，分別對每行突變，再把結果重新組合成子代解。

步驟八——局部搜索

1.從暫時組(步驟三產生)中隨機選擇N_elite個解，加入有(N_pop-N_elite)個解的當前種群，構造一個有N_pop個解的種群。

2.(對每個解)通過移動突變隨機產生k個鄰域解。

3.(對每個解)通過選擇該解的父代解的適應度函數加權值來構造該解的適應度函數，然后計算這k個鄰域解的適應度函數值。

4.(對每個解)如果這k個鄰域解中有比該解更優的解，則以之替換該解；否則，該解不做變化。

步驟九——迭代

1.如果算法已經搜索指定個數的解，則算法結束；否則返回步驟二。

步驟十——產生調度方案

1.迭代結束后，當前種群中的最優解和暫時組中的解即為算法所求得的優良解，根據調度方案的表示方式，即可將這些解轉換為對應的調度方案。