考慮新能源與電動汽車接入的主動配電網重構方法與流程

本發明屬于配電系統運行技術領域，具體涉及一種考慮新能源與電動汽車接入的主動配電網重構方法。

背景技術：

近年來，化石能源短缺、環境污染和全球氣候變化等問題引發世界范圍內的新能源革命。以風能、光伏發電為主要形式的分布式電源(Distributed Generation，DG)發展迅速，中國風電機組裝機容量計劃在2020年達到2億千瓦。這些新能源為緩解電能緊張、改善能源結構做出了巨大貢獻，受到廣泛重視和研究。電動汽車(Electric Vehicle，EV)也在減少碳排放，治理霧霾問題方面被寄予厚望，國內EV保有量預計于2020年達到50萬輛。

未來配電網絡具有分布式新能源和EV等柔性負荷滲透率較高的特點，其隨機性使得系統的運行狀態不確定，波動性較大，配電網的潮流計算變得更為復雜。常規的配電網重構方法如支路交換法、動態規劃法等一般只適應輻射型配電網，而含DG的配電網則是多端網絡，結構更復雜；且當DG和EV接入配電網后，配電網潮流的隨機性和復雜性大大增加，傳統重構方法對電源及負荷的隨機性考慮不足。人工智能算法能適應不同網絡結構，且在搜索全局最優解的方面表現較好，但受初始解影響較大。目前考慮DG和EV隨機性的配電網重構方法較少。

技術實現要素：

針對現有技術存在的不足，本發明提出了一種考慮新能源與電動汽車接入的主動配電網重構方法。

本發明采用基于時間尺度的場景分析法分割分布式電源出力(DG)出力和電動汽車(EV)負荷，利用劃分區間分割波動，繼而在各時間場景內利用隨機潮流分析計算配電網潮流，在不失準確性的前提下簡化了DG和EV的隨機性模型和潮流計算。

為解決上述技術問題，本發明采用如下的技術方案：

考慮新能源與電動汽車接入的主動配電網重構方法，包括步驟：

步驟1，構建風電隨機性模型和電動汽車隨機性模型；

步驟2，結合風電隨機性模型、電動汽車隨機性模型、目標函數和約束條件構建配 電網重構系統模型；

所述的目標函數為OF表示配電網系統有功損耗總期望值；p_b表示時間場景b出現的概率，即時間場景b的時間長度在一天時間的占比；L_b表示時間場景b下考慮電源及負荷隨機性的隨機潮流有功網損期望值；G為時間場景數；

所述的約束條件包括潮流約束、節點電壓約束、傳輸功率約束、網絡拓撲約束、以及風電和電動汽車充電站接入點的功率因素約束；

步驟3，根據各時刻用電情況將一天劃分為若干時間場景；

步驟4，基于配電網重構系統模型，采用改進的生物地理優化法搜索最優配電網絡結構。

步驟1具體為：

采用線性函數表示風力機的功率曲線位于切入風速和額定風速間的部分，獲得風電功率概率密度函數f(P_W)，采用高斯分布函數對f(P_W)進行近似，獲得風電隨機性模型f^*(P_Wi)＝αG(α₁,α₂,P_Wi)，其中，G(α₁,α₂,P_Wi)表示高斯分布函數，P_Wi表示風電有功出力；α、α₁、α₂分別為G(α₁,α₂,P_Wi)的系數、均值和方差，α根據地理信息確定。

步驟2中，所述的電動汽車隨機性模型包括電動汽車的充電起始時刻、充電功率、充電耗時、充電狀態的概率密度函數。

基于電動汽車充電起始時刻滿足正態分布，構建充電起始時刻的概率密度函數f_S(x₁)：

其中，x₁表示變量，這里x₁表示充電起始時刻；σ_S表示變量的方差；μ_s表示變量的均值；σ_S和μ_s用來描述充電起始時刻的分布特性，μ_S＝17.6，σ_S＝3.4。

基于電動汽車的充電功率在2～3kW范圍內滿足均勻分布，構建充電功率的概率密度函數

其中，x₂表示變量，這里x₂表示充電功率。

充電耗時的概率密度函數為：

其中，x₃表示變量，這里x₃表充電耗時；σ_D表示變量的方差；μ_D表示變量的均值；p表示積分變量；σ_D和μ_D用來描述電動汽車充電耗時的分布特性，μ_D＝3.2，σ_D＝0.88。

時刻t₀充電狀態的概率密度函數如下：

其中，表示充電狀態為1時的概率密度，表示充電狀態為0時的概率密度，1代表正在充電，0代表未在充電；t_s表示充電起始時刻；t_C表示充電時長；F_S和分別為充電起始時刻和充電耗時的概率分布函數。

步驟3具體為：

將一天劃分為6個時間場景，即0:00～6:00為第一時間場景，6:00～12:00為第二時間場景，12:00～13:00為第三時間場景，13:00～17:00為第四時間場景，17:00～21:00為第五時間場景，21:00～0:00為第六時間場景。

步驟5進一步包括子步驟：

5.1初始化參數；

5.2隨機初始化初始種群中各棲息地的適宜度向量x_i，i＝1,2,...,n；

5.3計算初始種群中各棲息地i的適宜度指數，適宜度指數最大的棲息地即個體最優解，其他棲息地則為非精英棲息地，適宜度指數f(x_i)即配電網系統有功損耗總期望值 OF，通過潮流計算獲得；

5.4對棲息地進行遷移操作，形成新種群，以新種群為當前種群，計算當前種群中各棲息地i的適宜度指數，獲得當前個體最優解和當前非精英棲息地；

5.5根據當前種群各棲息地的平均適宜度指數判斷是否陷入局部最優，若是，執行步驟5.6；否則，執行步驟5.7；

5.6計算當前種群各棲息地的變異率基于變異率對當前非精英棲息地進行突變操作，以突變后的種群為當前種群，計算當前種群中各棲息地i的適宜度指數，獲得當前個體最優解和當前非精英棲息地，然后執行步驟5.7；

5.7判斷是否達到最大迭代次數，若達到，則結束；否則，繼續執行步驟5.2。

步驟4中采用如下的編碼方法：

首先，使配電網絡結構中所有開關均閉合；

然后，對配電網絡結構中各環均進行一次解環操作；

接著，對可行解編碼獲得M維空間的點集，將初始棲息地也編碼為M維的點，M為配電網絡結構中的環數；每個可行解中，任何一個開關最多被打開一次，不同環路間的共用路徑上最多打開一個開關。

與現有技術相比，本發明具有以下優點和有益效果：

1)風電和EV的分場景隨機性模型能在保證精確性的前提下簡化模型，避免了場景的組合爆炸，體現了對于配電網中不斷增加的DG和EV的適應性；

2)場景分析和隨機潮流計算相結合的方法既能彌補場景分析法在精確性上的不足，又能有效限制隨機潮流計算中的波動誤差；

3)本發明采用改進的生物地理算法能快速收斂并避免早熟、陷入局部最優，在迭代次數較少的情況下就能搜尋到最優解，在收斂速度和收斂精度上表現出了相對與傳統的BBO算法、PSO算法、GA算法的優勢。

附圖說明

圖1為本發明方法的具體流程圖；

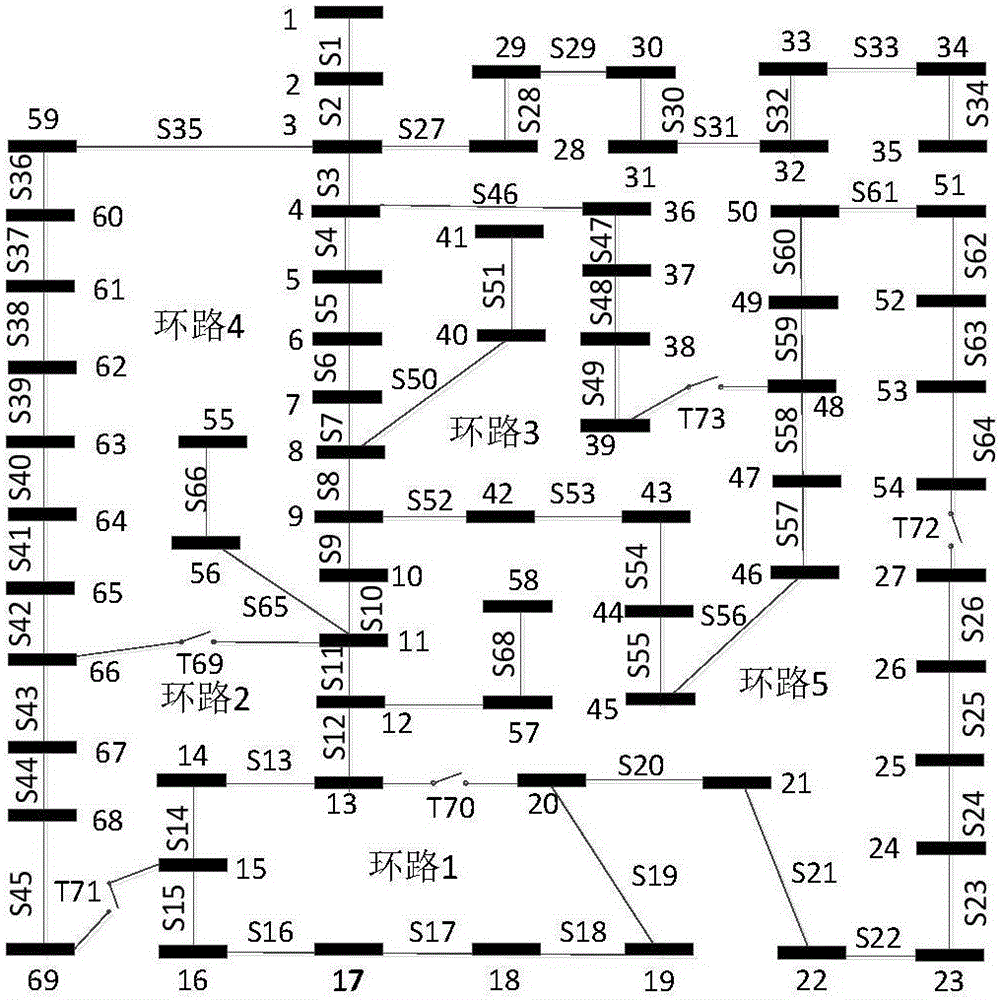
圖2為實施例中初始配電網絡結構示意圖；

圖3為實施例中重構后的配電網絡結構示意圖；

圖4為實施例中重構后各時間場景下節點電壓分布圖；

圖5為實施例中重構前后節點電壓期望值分布圖；

圖6為實施例中不同方法的重構效果對比圖。

具體實施方式

下面將結合附圖和具體實施方式進一步說明本發明技術方案。

見圖1，本發明具體步驟如下：

步驟1，建立風電隨機性模型。

當風力機的功率曲線位于切入風速和額定風速之間的部分用線性函數表示時，精確的風電功率概率密度函數f(P_W)如下：

式(1)中：

P_W表示風電出力；

P_rate表示風機的額定功率；

v_rate、v_co、v_ci分別表示額定風速、切入風速、切除風速；

F(v_co)、F(v_rate)、F(v_ci)分別為風速不大于v_co、v_rate和v_ci的概率；

k和c分別表示形狀參數和尺度參數；

k₁＝P_rate/(v_rate-v_ci)，k₂＝-k₁v_ci；

q_w為風電自身的強迫停運概率。

風電出力的精確概率密度函數模型見式(1)，但是該函數模型比較復雜，難以應用于實際的解析概率潮流計算中。為了兼顧其準確性與實用性，采用高斯分布函數對式(1)進行近似，獲得風電隨機性模型f^*(P_Wi)：

f^*(P_Wi)＝αG(α₁,α₂,P_Wi) (2)

式(2)中：

G(α₁,α₂,P_Wi)表示高斯分布函數，P_Wi表示風電有功出力；

α、α₁、α₂分別為G(α₁,α₂,P_Wi)的系數、均值和方差，α根據地理信息確定。

步驟2，建立電動汽車隨機性模型。

假設EV充電起始時刻是獨立的隨機變量，滿足如下正態分布，充電起始時刻的概率密度函數f_S(x₁)為：

式(3)中：

x₁表示變量，這里x₁表示充電起始時刻；

σ_S表示變量的方差；

μ_s表示變量的均值；

σ_S和μ_s用來描述充電起始時刻的分布特性，μ_S＝17.6，σ_S＝3.4。

EV的充電功率P_C在2～3kW范圍內滿足均勻分布，即充電功率的概率密度函數為：

式(4)中，x₂表示變量，這里x₂表示EA的充電功率。

EV充電耗時的概率密度函數為：

式(5)中：

x₃表示變量，這里x₃表示EA的充電耗時；

σ_D表示變量的方差；

μ_D表示變量的均值；

p表示積分變量。

σ_D和μ_D用來描述電動汽車充電耗時的分布特性，μ_D＝3.2，σ_D＝0.88。

EV在時刻t₀的充電狀態用變量表示，值可以為1或0，1代表正在充電，0代表未在充電。充電狀態的概率密度函數如下：

式(6)～(7)中：

表示充電狀態為1時的概率密度；

表示充電狀態為0時的概率密度；

t_s表示充電起始時刻；

t_C表示充電時長；

F_S和分別為充電起始時刻和充電耗時的概率分布函數。

步驟3，結合風電隨機性模型和電動汽車隨機性模型，建立配電網重構系統模型。

配電網重構的優化目標一般是最小化系統有功網損，考慮到DG和EV接入的隨機性，配電網系統有功網損可采用概率分布函數來逼近真實情況。因此，本發明以配電網系統有功網損期望值最小為目標函數構建配電網重構系統模型，所述的配電網重構系統模型包括風電隨機性模型、電動汽車隨機性模型、目標函數和約束條件。

配電網重構系統模型的目標函數如下：

式(8)～(9)中：

OF表示配電網系統有功損耗總期望值；

p_b表示時間場景b出現的概率，即時間場景b的時間長度在一天時間的占比，p_b＝T_b/24，T_b表示時間場景b的時間長度，單位：小時；

L_b表示時間場景b下考慮電源及負荷隨機性的隨機潮流有功網損期望值；

G為時間場景數；

r_a為支路a的電阻，l表示支路數；

P_ab、Q_ab、U_ab分別為支路a在時間場景b下的有功功率、無功功率和電壓。

配電網重構系統模型的約束條件包括潮流約束、節點電壓約束、傳輸功率約束、網絡拓撲約束、以及風電和電動汽車充電站接入點的功率因素約束。

風電和電動汽車充電站接入點的功率因數約束如下：

式(13)～(11)中：F_w表示風電接入點的功率，F_EV表示電動汽車充電站接入點的功率；和分別為風電接入點的功率下限和上限，和分別為電動汽車充電站接入點的功率下限和上限。

其他約束條件均為配電網重構系統模型采用的常規約束條件，在此不作贅述。

步驟4，基于時間尺度進行場景劃分，獲得時間場景。

根據一天的用電曲線將一天劃分為多個時間場景，各時間場景內的用電曲線無明顯變化。用電曲線包括普通負荷曲線、特殊負荷曲線和DG功率曲線，普通負荷進一步包括居民用電、工業用電、商業用電和農村用電，特殊負荷即電動汽車用電。

本步驟中，根據經驗劃分時間場景，劃分方式并不唯一。具體可基于普通負荷曲線、特殊負荷曲線和DG功率曲線將一天劃分為多個時間場景，時間場景內各曲線的變化幅度均應小于對應的預設值，預設值根據實際情況和經驗人為設定。

具體實施中，將一天劃分為6個時間場景，即，0:00～6:00時間段為第一時間場景，6:00～12:00時間段為第二時間場景，12:00～13:00時間段為第三時間場景，13:00～17:00時間段為第四時間場景，17:00～21:00時間段為第五時間場景，21:00～0:00時間段為第六時間場景。

步驟5，基于配電網重構系統模型，采用基于改進的生物地理優化法搜索最優配電網絡結構。

本步驟依次包括如下子步驟：

(1)設置最大迭代次數，初始化種群規模n、優化問題維度D、棲息地種群最大容量S_max、遷入率函數最大值I、遷出率函數最大值E、最大變異率m_max、遷移率P_mod和 精英個體留存數z。

(2)隨機初始化初始種群中各棲息地的適宜度向量x_i，i＝1,2,...,n，各適宜度向量均對應一個配電網絡結構，即配電網重構系統模型的潛在解。

(3)計算初始種群中各棲息地i的適宜度指數f(x_i)，適宜度指數f(x_i)最大的棲息地即個體最優解，其他棲息地則為非精英棲息地。適宜度指數f(x_i)即對當前配電網絡結構進行潮流計算得到的系統有功網損總期望值，即公式(8)中的OF，

(4)采用余弦遷移模型對棲息地進行遷移操作，形成新種群，以新種群為當前種群，計算當前種群中各棲息地i的適宜度指數，獲得當前個體最優解和當前非精英棲息地；

(5)根據當前種群各棲息地的平均適宜度指數的方差判斷是否陷入局部最優，若是，執行步驟(6)；否則，執行步驟(7)。

(6)通過公式計算當前種群各棲息地的變異率，基于變異率對當前非精英棲息地進行突變操作，用m(s_i)判斷棲息地i的某個特征分量是否進行突變，以突變后的種群為當前種群，計算當前種群中各棲息地i的適宜度指數，獲得當前個體最優解和當前非精英棲息地，然后執行步驟(7)。其中，s_i表示第i個棲息地的種群數量，m(s_i)表示第i個棲息地的的變異率，m_max為最大變異率，P(s_i)指第i個棲息地的種群數量為s_i的概率，P_max為最大概率。

(7)判斷是否達到最大迭代次數，若達到，則結束；否則，繼續執行步驟(2)。

本步驟中，本發明提出了一種適用于重構模型求解的編碼方法，具體如下：

對于有M個環的配電網絡結構，第j個環的開關數記為k_j，j＝1,2,...M。將第j個環中第p個開關編碼為S_jp，那么該配電網絡結構的可能樹狀結構就有種。求解時，首先，使配電網絡結構中所有開關均閉合；然后，對配電網絡結構中各環均進行一次解環操作，即在各環中分別選取一個開關將其解環，這樣對可行解進行編碼可以得到一個M維空間的點集，將初始棲息地編碼為M維的點，這個點就包含了配電網網絡結構信息。

在配電網絡結構較復雜、不同環間無共用路徑時，上述編碼方法可能導致求解結果違背連通性約束或者導致形成新的環。因此，本步驟中還添加了兩條編碼方法來解決上述問題：

a、每個可行解中，任何一個開關最多被打開一次；

b、每個可行解中，不同環路間的共用路徑上最多打開一個開關。

下面通過實施例進一步說明本發明。

以IEEE69節點配電系統為例，結構見圖2，風力機接入點為節點10、19、23和69，EV充電站接入點為節點34、53、58、67。風電機組的切入風速、額定風速、切出風速分別為3m/s、14m/s、25m/s，c和k分別為9.19和1.93。算例原始的負荷量為3.8MW，加入的EV負荷峰值為2MW，風電出力峰值為3MW。

利用IBBO算法對建立的配電網重構系統模型進行求解，算例初始配電網絡結構圖見圖2，經重構后的配電網絡結構圖見圖3，重構前后配電網絡結構數據對比見表2。圖4～5分別給出了各時間場景下重構后和重構前的節點電壓點電壓期望值分布圖。

表2 重構前后的配電網絡結構數據

分別采用本發明方法、粒子群法、遺傳法和模擬退火法對圖2所示配電網絡結構進行重構，最大迭代次數均為20，不同方法重構結果對比見圖6和表3。從表3可以看出本發明方法搜索的最優配電網絡結構的網絡損耗平均值和均方差均最低，說明本發明方法重構結果優于其他方法，且收斂程度好，結果誤差低。

表3 不同方法的重構效果比較

本文中所描述的具體實施例僅僅是對本發明精神作舉例說明。本發明所屬技術領域的技術人員可以對所描述的具體實施例做各種各樣的修改或補充或采用類似的方式替代，但并不會偏離本發明的精神或者超越所附權利要求書所定義的范圍。