模擬小展弦比飛行器不可壓縮旋流場的數值方法與流程

本發明涉及計算流體力學(CFD：ComputationalFluidDynamics)領域中的一種數值方法，具體是一種模擬小展弦比飛行器不可壓縮旋流場的數值方法。
背景技術：
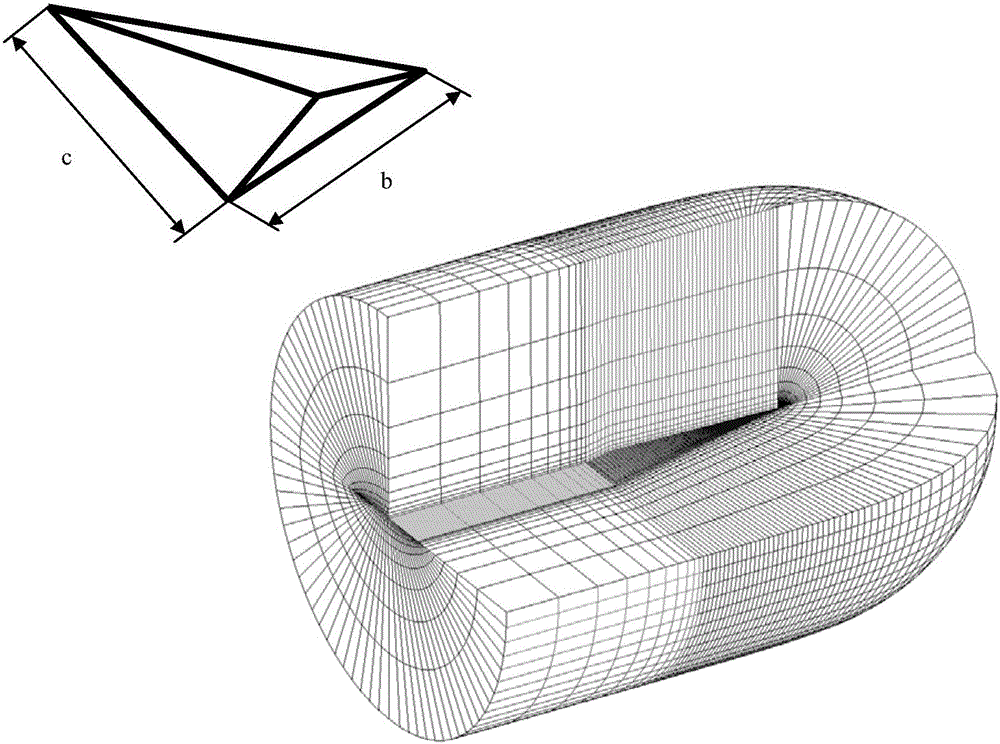
：計算流體力學綜合了流體力學、應用數學、計算機科學，是一門應用性極強的學科。流體力學問題的數值模擬以其低成本、直觀性強的優勢，在流體流動的機理探索、工業產品設計等各個相關領域占據重要地位。計算流體力學面臨的最大的問題和挑戰之一即是如何提高數值模擬的精度，降低誤差，忠實地表現流體流動的特性。影響流體力學問題的數值模擬的精度的重要因素之一是：當使用數值方法求解流體控制方程，即歐拉(Euler)方程或者納維爾-斯托克斯(Navier-Stokes)方程時，會產生數值耗散(numericaldiffusion)，造成數值解的誤差。例如數值方法中對控制方程的對流項的空間離散方法(如中心差分、迎風差分)、時間離散方法(如顯示時間積分、隱式時間積分)、湍流模型(如雙方程模型、大渦模擬)的使用，以及計算網格正交性都會產生不同程度的數值耗散。此外，數值模擬中還經常要使用一種人工數值耗散(artificialdiffusion)技術，其目的是通過適當降低計算精度而獲得穩定的數值解。例如流場中的不連續(discontinuity)界面的捕捉，如激波(shock)的捕捉，即是依靠加入適量的人工耗散項，以避免數值解在流動變量梯度較大的地方出現數值振蕩現象。數值耗散可以理解為是流場中的一種能量損失，這種能量損失在某種程度上使得數值模擬結果不能忠實的體現流體的流動特性，降低了計算精度。先進的數值方法應該是在保證獲得穩定性的數值解的前提下，將數值耗散減至最小。數值耗散對流場的數值模擬結果的最明顯的影響體現在對流動變量的間斷界面的捕捉。如前所述，激波是強間斷界面，對其捕捉必須加入一定的人工數值耗散。因為激波前后存在熵增，即能量的損失，所以，通過加入人工數值耗散捕捉激波具有合理的物理意義。但是，過大的數值耗散會使數值解獲得的激波界面變得模糊，降低了數值解對激波強度和空間位置的預測精度。流場中存在另一類流動不連續現象，即接觸不連續(contactdiscontinuity)。相對激波而言，接觸不連續的特點是弱不連續，跨過不連續界面，壓力和法向速度是連續的。工程實踐中，這種類型的流動現象大量存在。例如，流場中鈍體后方的渦脫落、自由剪切流的流動等等。數值模擬中對于這種接觸不連續的捕捉更加困難，因為數值方法中的數值耗散 即使很小也會使弱不連續界面變得模糊，降低數值解對流場的預測精度，這也是旋流場(Vortex-dominatedFlows)的數值模擬技術成為CFD領域的重大挑戰的原因。為了提高旋流場的數值模擬的精度，一種方法是加密計算網格，在更加細小的空間尺度內求解流體控制方程。加密計算網格首先會使計算量加大，增加計算成本。此外，數值計算的誤差隨著計算網格的增加會不斷積累，在一定程度上造成相反的效果。另一種方法是在流場中采用物理模型來增加流場中描述旋流流動的變量—渦量(vorticity)的強度。例如在流場中加入點渦模型，可以人為地增加渦量；或者在流場局部直接求解渦量方程，以減小渦量的輸運過程中的耗散。但是，這些方法在應用上仍受到一定限制。點渦模型是在預先明確旋渦發生位置的前提下才能使用，僅適合一些簡單的流動現象。除了二維不可壓縮正壓流場，渦量方程比與欲求解的Euler，Navier-Stokes方程更為復雜。二十世紀初期，提出了一種提高不可壓縮(incompressible)旋流場的求解精度的數值方法，渦量限制法(VorticityConfinement)。該方法的原理是在流體控制方程的動量方程中的源項位置，加入一個渦量形式的體積力項，從數值耗散中將渦量減去，克服數值耗散造成的旋渦場的接觸不連續界面的模糊，從而更精確地捕捉旋渦結構，實現提高旋渦場的計算精度的目的。渦量限制法的具體內容如下：首先寫出不可壓縮、無粘流的控制方程，包括連續方程和動量方程，分別為▿·V→=0,---(1)]]>∂V→∂t+(V→·▿)V→+1ρ▿p=B→,---(2)]]>式中，V是速度矢量，包含直角坐標系下的三維i，j，k分量u，v，w；ρ、p、t分別是密度、壓力和時間。式中算子表示為符號·代表內積計算。動量方程(2)的右邊是體積力項形式的源項按照渦量限制法中的定義B→=n→c×ω→,---(3)]]>式中，代表渦量，在直角坐標系下有按照渦量的定義，ω→=▿×V→=ijk∂∂x∂∂y∂∂zuvw=(∂w∂y-∂v∂z)i+(∂u∂z-∂w∂x)j+(∂v∂x-∂u∂y)k;]]>式中符號×代表叉乘運算，代表渦量梯度變化的方向，即n→c=▿φ|▿φ|,---(4)]]>其中，φ是渦量的模；是渦量的模的梯度的模，即φ=|ω→|=ωx2+ωy2+ωz2,---(5)]]>|▿φ|=(∂φ∂x)2+(∂φ∂y)2+(∂φ∂z)2.---(6)]]>動量方程(2)中的源項需要公式(3)中的乘以一個比例因子ε，則B→=ϵ(n→c×ω→),---(7)]]>其物理意義是指向渦量中心的力。Steinhoff的原始的渦量限制法中給出ε為常數，為0.01-0.05，其作用是用來調整渦量限制的大小。該方法形式簡單，不需要加密計算網格，在旋流場的數值模擬中得到廣泛應用。對該方法在隨后的改進主要集中在參數ε的表達。渦量限制法是依靠在流場中加入限定的渦量以抵消數值耗散的原理來模擬旋流場的流動狀態。盡管該方法在捕捉不可壓縮流場中的接觸不連續的方面已經取得了明顯的改進效果，但存在以下缺陷：1.對加入的渦量調整完全靠系數ε；2.加入的渦量的空間離散精度是被限定的，無法進一步提高；3.源項對動量方程的數值解的收斂的穩定性影響是不確定的。為了更加精確地模擬不可壓縮流的旋渦運動，需要進一步改進對于流場中接觸不連續的捕捉機制。一種途徑是根據不可壓縮流的特點，改進在流場中通過加入渦量來抵消數值耗散的內在工作機理，通過保持渦量的精度，更精確地用模擬流場中的旋渦運動，形成一種新的不可壓縮流的旋渦運動的數值模擬技術，渦量保持技術(VorticityRefinement)。該技術可以使渦量的空間離散具有高階精度的格式，同時該可以利用源項增進收斂進程的穩定性。小展弦比飛行器外形的特征主要在于，其機翼的展長相對較小。這類飛行器升力高、轉彎半徑小，常見于一類戰斗機系列。和其他普通類的飛行器相比，小展弦比飛行器機翼在高攻角飛行時容易在機翼上方表面生成大強度的機翼前緣的翼尖渦，形成強旋流流場，會對飛行器的操縱性產生重大影響。因而對這類飛行器的不可壓縮旋流場精確地模擬有重要的意義。技術實現要素：本發明涉及計算流體力學領域中一種模擬小展弦比飛行器不可壓縮旋流場的數值方法，具體是根據不可壓縮流的特點，在流場中通過加入兩種不同形式的渦量力來抵消數值耗散的數值方法。該方法可以使加入的渦量的空間離散具有高階精度的格式，通過保持渦量的精度，更精確地用模擬流場中的旋渦運動，是一種新的不可壓縮流的旋渦運動的數值模擬技術—渦量保持技術(VorticityRefinement)。本發明采用的技術方案：如公式(2)表示的，渦量限制法中在不可壓縮流動的動量方程的等號右邊加入了一個體積力項，它代表渦量在其變化梯度相反的方向的受力，如公式(7)所示。實際上，如果將公式(4)帶入公式示(7)并運用算子的運算規律可得B→=ϵ(n→c×ω→)=ϵ▿φ|▿φ|×ω→=ϵ▿×(φ|▿φ|ω→)-ϵφ|▿φ|(▿×ω→).---(8)]]>在上式中再次運用算子的運算規律可得▿×ω→=▿×(▿×V→)=▿(▿·V→)-▿2V→,---(9)]]>式中是拉普拉斯算子，定義為又根據公式(1)不可壓縮流的連續方程，將公式(9)代入公式(8)，可得B→=ϵ▿×(φ|▿φ|ω→)+ϵφ|▿φ|(▿2V→).---(10)]]>對于不可壓縮流，公式(10)與公式(7)完全等價。現將公式(10)中的重新寫成如下形式，即B→=B→1+B→2,---(11)]]>其中，B→1=ϵ1▿×(φ|▿φ|ω→),---(12)]]>因為是螺旋度的定以，所以被稱作渦量在變化梯度方向的螺旋力；B→2=ϵ2φ|▿φ|(▿2V→),---(13)]]>因為拉普拉斯算子的耗散特性，被稱作在渦量在變化梯度方向的粘性耗散力。至此公式(2)中以動量方程的源項形式表示的渦量在其變化梯度相反的方向的受力(渦量限制)限制被分解為兩部分，形成兩種力的形式。其中渦量在變化梯度方向的螺旋力與渦量的變化方向和渦量大小有關；而渦量在變化梯度方向的粘性耗散力僅與渦量的變化梯度方向有關。圖1給出兩種形式的力的形成原理和關系圖。圖中表明，由渦量和渦量梯度變化的方向向量構成平面1，被稱作渦量作用平面。原始的渦量限制與該平面垂直，并與它的兩個分量，渦量在變化梯度方向的螺旋力和渦量變化梯度方向的粘性耗散力共同構成平面2，被稱作渦量限制平面。平面1垂直與平面2。和的夾角被稱作螺旋角，該夾角的余弦即為渦量限制被分解后形成的兩種形式的力，和將在數值方法中起到不同的作用。公式(12)和(13)中是用了兩個參數：ε1和ε2，分別作為不同的兩個力的放大系數。如果ε1和ε2相等，且等于公式(7)中的ε，則成為同向渦量限制(isotropicvorticityconfinement)，其效果等同于公式(7)表示的原始的渦量限制；而ε1和ε2不相等時，成為異向渦量限制(anisotropicvorticityconfinement)。而不可壓縮旋流場的數值模擬精度的提高可以通過異性渦量限制獲得。如公式(12)所示，渦量在變化梯度方向的螺旋力與渦量的變化方向和渦量大小有關，數值解中需要高精度的空間離散，以提高模擬精度。源項中的被移動等號左邊后，可以利用高斯定理，將控制體單元內的體積力形式轉變為表面通量的積分形式。有限體積法(FiniteVolumeMethod)中，某一控制體單元，即某一計算網格的體積為Ω，而其表面積為面積元為dS。根據高斯定理，可將體積積分變換為面積積分，則渦量在變化梯度方向的螺旋力從體積積分變為面積積分的過程可表示為∫ΩB→1dΩ=∫Ωϵ1▿×(φ|▿φ|ω→)dΩ=∫∂Ωϵ1n→×(φ|▿φ|ω→)dS,---(13)]]>其中計算網格邊界的單位向量。于是，在計算網格邊界上產生了一個由于渦量在變化梯度方向的螺旋力產生的向量，被稱作渦量的螺旋力向量F→ω=ϵ1n→×(φ|▿φ|ω→).---(14)]]>在數值解的求解過程中，可以對該向量在計算網格邊界上進行高階精度的空間離散。由于該向量與渦量的變化方向和渦量大小有關，為進一步提高了旋渦流場的空間模擬精度提供了可能性。例如可以同過流動變量的高階插值獲得計算網格界面上用來計算向量的值。此外，如果適當增大ε1、減小ε2，意味著增大渦量在變化梯度方向的螺旋力、降低渦量變化梯度方向的粘性耗散力，即采用異向渦量限制，利用調節這兩個力的內部關系的機制，可以進一步調整旋渦運動中的接觸不連續界面的捕捉效果。總之，本發明提出的提高可壓縮旋流場的數值模擬精度的數值方法包括四個技術元素，分別為：1.將渦量限制法中的源項分解稱為兩個力，渦量在變化梯度方向的螺旋力和渦量變化梯度方向的粘性耗散力，并將渦量在變化梯度方向的螺旋力移動到不可壓縮流的動量方程的等號左變；2.通過高斯定理將計算網格內渦量在變化梯度方向的螺旋力轉化為計算網格邊界上的上的力，進行高精度的空間離散，按照通量進行計算；3.渦量在變化梯度方向的螺旋力和渦量變化梯度方向的粘性耗散力采用不同的放大系數，即采用異向的渦量限制。該數值方法被稱為可壓縮旋流場的渦量保持技術(VorticityRefinement)。本發明的優點：本發明提出的提高不可壓縮旋流場的數值模擬精度的數值方法是根據不可壓縮流的特點，通過加入兩種不同形式的力來改進在流場中抵消數值耗散的內在工作機制，通過保持渦量的精度，更精確地模擬流場中的旋渦運動。該方法使計算網格內的渦量在變化梯度方向的螺旋力轉化為計算網格邊界上的上的力，可以使其空間離散具有高階精度的格式。這兩個力采用不同的放大系數，可以進一步保持渦量的精度，更精確地模擬一類小展弦比飛行器不可壓縮旋流場流場的旋渦運動。附圖說明圖1渦量在變化梯度方向的螺旋力和渦量變化梯度方向的粘性耗散力形成原理和關系圖圖中，1：渦量作用平面、2：螺旋角、3渦量限制平面。圖2三角機翼的外形和計算網格。圖3數值方法的驗證，即異向渦量限制效果的比較。具體實施方式以下以一個具體實施方案進一步說明本發明提出的小展弦比飛行器不可壓縮旋流場的數值模擬方法，這種數值模擬技術可以用Fortran90計算機高級程序語言實現，并通過計算機運行來模擬三維三角機翼在高攻角低速飛行狀態下的周圍流場。具體實施方案中，采用小展弦比的三角機翼在高攻角下的不可壓縮流場。大量實驗表明三角機翼在高攻角下飛行，其周圍的流場是以旋渦運動為主的流場。三角翼根弦長為c、翼展為b，展弦比為1。計算網格采用多塊結構化適體六面體網格，機翼周圍采用O-型網格，圍繞機翼剖面方向192個網格；法線方向68個網格；翼展方向96個網格。圖2表示了三角機翼的幾何形狀和圍繞三角機翼生成的計算網格。數值模擬的空間離散采用有限體積法(FiniteVolumeMethod)，每個計算網格成為控制單元，流動變量在控制單元的中心。數值模擬的飛行條件是：來流速度：57m/s大氣壓力：100kPa大氣密度：1.2kg/m3攻角：20°不可壓縮無粘流的動量方程，即方程(2)中不計粘性項本發明中要求加上在計算網格邊界上產生了一個由于渦量在變化梯度方向的螺旋力產生的向量意味著在動量方程左邊的對流項后面加上這個向量，在等號右邊，即源項的位置加上渦量變化梯度方向的粘性耗散力按照三維守恒的積分形式重新寫出動量方程，∂∂t∫ΩV→dΩ+∫∂Ω(F→c-F→ω)dS=∫ΩB→2dΩ,---(15)]]>其中，守恒變量對流項向量和渦量的螺旋力向量(見公式(19))分別為V→=uvw;F→c=uV+nxp/ρvV+nyp/ρwV+nzp/ρ;F→ω=ϵ1φ|▿φ|ωzny-ωynzωxnz-ωznxωynx-ωxny.---(16)]]>上式中，密度ρ為一固定值；V代表速度不變量，是網格邊界的外法線向量與速度向量的點乘，即V≡V→·n→=nxu+nyv+nzw;---(17)]]>可以將對流項向量和渦量的螺旋力向量寫成展開形式，F→c=u2+p/ρuvuwnx+uvv2+p/ρvwny+uwvww2+p/ρnz.---(18)]]>對流項經壓力分離后，可以寫成不計壓力的對流項向量和壓力向量之和，顯然有，F→c=F→cV+F→cp,---(19)]]>其中，F→cV=u2uvuwnx+uvv2vwny+uwvww2nz;---(20)]]>F→cp=p/ρ00nx+0p/ρ0ny+00p/ρnz.---(21)]]>進一步可以寫出本發明提出的渦量在變化梯度方向的螺旋力向量和源項形式的渦量變化梯度方向的粘性耗散力的具體形式分別為，F→ω=ϵ1φ|▿φ|0∂u∂y-∂v∂x∂u∂z-∂w∂xnx+ϵ1φ|▿φ|∂v∂x-∂u∂y0∂v∂z-∂w∂yny+ϵ1φ|▿φ|∂w∂x-∂u∂z∂w∂y-∂v∂z0nz;---(22)]]>B→2=ϵ2φ|▿φ|∂2u∂x2+∂2u∂y2+∂2u∂z2∂2v∂x2+∂2v∂y2+∂2v∂z2∂2w∂x2+∂2w∂y2+∂2w∂z2,---(23)]]>其中，渦量的模φ和渦量的模的梯度的模由公式(5)和(6)給出。公式(22)和(23)中涉及的一階導數和二階導數項均可利用格林公式求取或者直接按照泰勒展開求取，其過程是公知的，不再敘述。以下是在同位網格(CollocatedGrid)中運用基于壓力的方法(Pressure-BasedMethod)求解包含渦量在變化梯度方向的螺旋力向量和渦量變化梯度方向的粘性耗散力的不可壓縮流控制方程的過程。首先將公式(15)寫成離散形式，(V→t+Δt-V→Δt)Ωi,j,k+ΣmNF(F→cV+F→cp-F→ω)mΔSm=(B→2Ω)i,j,k,---(24)]]>其中，Ωi,j,k代表空間任一離散控制體體積；△t代表積分時間步長；代表流場更新后速度；△Sm代表控制體任一表面面積；NF代表控制體表面個數，三維情況下為6。重新整理右手項，有R→(V→)=ΣmNF(F→cV-F→ω)mΔSm-(B→2Ω)i,j,k+ΣmNF(F→cp)mΔSm;---(25)]]>而使用一個假設的初始速度計算一個不計壓力項的右手項即R→c(V→*)=ΣmNF[F→cV(V→*)-F→ω(V→*)m]ΔSm-B→2(V→*)Ωi,j,k,---(26)]]>顯然有，R→(V→)=R→c(V→*)+ΣmNF(F→cp)mΔSm.---(27)]]>不計壓力項時候，可以從公式(31)獲得這個個初始速度場V→*=V→-ΔtΩi,j,kR→c(V→),---(28)]]>其中需要在計算網格邊界m上的不計壓力的對流項向量渦量在變化梯度方向的螺旋力向量以及在計算網格內的渦量變化梯度方向的粘性耗散力再帶入公式(26)以獲得不計壓力的右手項在按照公式(22)計算網格邊界m處的渦量在變化梯度方向的螺旋力向量的時候，對于其中的一階導數項采用高精度離散方法，例如在i-方向的三階空間離散表示為，∂u∂x=2ui+1+3ui-6ui-1+ui-26Δx.---(29)]]>網格中心點的初始速度在計算網格邊界上利用公知的MUSCL方法進行二階精度插值，可獲得在網格邊界m上的速度因而，根據公式(28)不計壓力項的情況下，在邊界m處的速度表示為V‾→m*=V→m*-ΔtΩ*mR→c(V→m*),---(30)]]>其中，是包含網格邊界m的輔助網格的體積。在邊界m處，考慮壓力項的速度為V→m=V→m*-ΔtΩi,j,kR→c(V→m*)-ΔtΩi,j,kR→pm,---(31)]]>其中，是公式(25)在網格邊界m處的值，任然用MUSCL方法進行二階插值獲得。整理公式(370)和(31)，有V→m=V‾→m*-ΔtΩmR→pm.---(32)]]>考慮壓力項的速度應該滿足不可壓縮流的連續方程(1)，即將連續方程(1)寫成離散形式，ΣmNFV→mΔSm=0.---(33)]]>將公式(32)帶入(33)，有ΣmNF(V‾→m*-ΔtΩi,j,kR→pm)ΔSm=0.---(34)]]>求解方程(34)，即可獲得t+△t時刻，流場的計算網格邊界m處的速度和壓力值pm， 這兩個值可以通過集合平均處理，轉化為計算網格中心處的值。圖3給出數值方法的驗證。表明異向渦量限制效果的比較，圖中表明了兩種方法計算的三角機翼上部渦量云圖。采用本發明提出的異向渦量限制，ε1＝0.07、ε2＝0.03比采用同向渦量限制，ε＝0.05時可以捕捉到更強的渦量，原因在于采用了高階精度離散和較大的放大系數。當前第1頁1 2 3