一種高強鋼輪輻中心孔翻邊沖模錐角角度優化方法與流程
本發明屬于車輪輪輻制造領域,具體是一種高強鋼輪輻中心孔翻邊沖模錐角角度優化方法。
背景技術:
車輪輪輻是連接汽車輪輞和輪轂的主要連接件,也是車輪安全的關鍵部件,制造輪輻傳統的材質主要有鋁合金和低碳鋼。隨著汽車工業對安全性能和產品輕量化要求的不斷提高,高強鋼由于具有較低的屈強比、成本較輕質材料低等在安全性和經濟性方面的優點而廣泛應用于輪輻成形。
傳統的鋼制輪輻成形工藝有沖壓和旋壓兩種。沖壓成形工藝以生產效率高、生產成本低以及適合批量生產等特點而被廣泛應用于鋼制輪輻的成形。為了使輪輻最終能夠和車軸實現連接,輪輻的沖壓成形工藝中包括一道重要的成形工序——中心孔翻邊。然而,由于輪輻的中心孔翻邊變形量很大,生產時為了提高效率又往往將其與其他工序復合采用而使鋼板的翻邊變形受到額外的影響,從而導致輪輻的中心孔翻邊在成形時經常出現翻邊開裂等缺陷,從而報廢零件,嚴重影響了鋼制輪輻的成品率。
隨著軋制工藝的發展和汽車工業的需求,強度高、成形難度大的高強鋼板料在輪輻制造業的應用越來越廣泛。高強鋼板料在用于輪輻沖壓成形時,由于其強度高,成形范圍窄,導致成形難度大且成形質量不易控制;再加上輪輻中心孔翻邊本身存在的特點,使得高強鋼輪輻的中心孔翻邊極易出現減薄等缺陷。目前,工廠減少輪輻中心孔翻邊開裂主要通過改變中心孔沖模的形狀,從而改善材料的流動情況而減輕開裂現象的發生。工廠中使用的中心孔翻邊沖模形狀主要有:錐形沖模、柱形沖模和拋物線沖模。在諸多形狀的中心孔翻邊沖模中,柱形沖模對翻邊開裂的改善不大,而拋物線沖模加工較為困難。因此,錐形沖模相較其他兩種沖模形狀在實際生產中獲得了更廣泛的應用。然而,對于錐形沖模,如何獲取其錐角角度是一個難題。現有的設計往往根據設計者經驗,或者依靠反復試錯法,存在周期長、成本高、結果不夠準確等缺點,這就導致錐形沖模無法獲得最優錐角進而減輕高強鋼輪輻中心孔翻邊時存在的開裂現象。目前,在沖壓模具角度優化領域,專利(CN 103357734 A)為了減輕筒形件拉深時的開裂情況,提出了一種用于錐形壓邊圈進行壓邊的模具設計方案,同時給出了獲取錐形壓邊圈最優錐角角度的優化方法,以實現在模具設計變量和材料特性給定情況下得到最優的錐角角度進而提供實用的筒形件拉深錐形壓邊配套模具。然而,輪輻中心孔翻邊過程中沖模錐角角度優化尚不存在科學的指導方法。為此,急需開發一種高效準確的鋼制輪輻中心孔翻邊沖模錐角角度優化方法,為實際生產通過改變錐角角度減輕開裂提供指導,推動高強鋼輪輻成形工藝的發展。
技術實現要素:
本發明的目的在于提供一種高強鋼輪輻中心孔翻邊錐形沖模錐角角度的優化方法,主要解決高強鋼輪輻中心孔翻邊時存在的翻邊開裂等技術問題。本發明的思路:通過建立正確的有限元模型模擬實際輪輻中心孔翻邊過程,選擇合適的韌性斷裂準則描述翻邊成形時材料的開裂行為,并通過設計合適的算法,進行錐角角度的優化,從而將錐角的角度從預先設定的一個寬區間優化縮小為長度小于設定標準的目標區間,所獲區間為理論最優錐角角度所在區間。同時有限元數值模擬技術的應用能提高優化效率,節約成本,實現精確優化。
為達到上述目的,本發明的技術方案是:一種高強鋼輪輻中心孔翻邊沖模錐角角度優化方法,包括以下步驟:
(1)建立高強鋼輪輻中心孔翻邊成形的三維有限元模型并驗證可靠性:
收集記錄實際生產中中心孔翻邊所在的成形工序的模具形狀尺寸,在有限元模擬軟件中建立不同模具和板料的幾何模型;根據單向拉伸試驗獲得所用高強鋼材料的力學性能參數,同時,為了描述中心孔翻邊開裂現象,選擇合適的韌性斷裂準則并將其耦合到本構關系中,從而建立起材料模型;
根據實際輪輻成形工序的相關參數,完成有限元建模的其他部分,如:幾何模型裝配、邊界條件和摩擦的設定、網格的劃分等;
驗證模型可靠性,計算高強鋼輪輻中心孔翻邊所在成形工序中變形體動能與內能的比值以及偽應變能與內能的比值,若所述動能與內能的比值在成形過程中不超過預期的數值,則可以認為板料變形在準靜態下發生的,即模型是穩定的;同時,為進一步驗證計算模型的正確性,將輪輻的仿真結果與實際生產所獲輪輻成形件結果作對比,若輪輻相關尺寸的仿真結果與所給尺寸相吻合,則驗證了所建立模型的正確性;
如果發現模型能量比不穩定或者模擬成形后尺寸與給定尺寸相差較大,則返回步驟重新建模、調試,直至模型滿足要求。
(2)選定優化初始角度θ1,優化區間長度θK和優化標準θt,優化初始角度θ1一般即為工廠按照經驗等預先設計的沖模錐角角度;優化區間長度θK一般選為以θ1為中心,左右各取相同長度構成一個區間;優化標準θt為一個短區間,體現了優化區間長度的優化程度,其越小表示優化程度越大,同時計算量越大。
(3)生成第一個優化區間,此時,K1為以θ1為中心,長度為θK的一個區間;生成優化角度序列。
(4)采用所建立的有限元模型,將模型中沖模幾何模型的錐角角度按照優化角度序列中角度進行設定,并進行模擬計算,獲得優化角度序列中每個角度所對應的損傷值,并生成損傷值序列D=(D1,D2,D3,D4,D5),對比損傷值序列中的損傷值,取最小的D值對應的角度,記為θ2;判斷此時下一個優化區間長度θK是否小于等于優化標準θt,如果是,則生成并輸出下一個優化區間K2,作為優化目標區間,如果為否,則進行下一次優化。(為了繼續說明本發明,此處假定優化區間長度大于優化標準)。
(5)生成第二個優化區間,此時,K2為以θ2為中心,長度為θK的一個區間;生成優化角度序列。
(6)采用所建立的有限元模型,將模型中沖模幾何模型的錐角角度按照優化角度序列設定,進行模擬計算,獲得優化角度序列中每個角度所對應的損傷值,并生成損傷值序列D=(D1,D2,D3,D4,D5),對比損傷值序列中的損傷值,取最小的D值對應的角度,記為θ3;判斷此時下一個優化區間長度θK是否小于等于優化標準θt,如果是,則生成并輸出下一個優化區間K3,作為優化目標區間,如果為否,則進行下一次優化。按上述生成優化區間的步驟采用所建立的有限元模型循環操作直至下一步。
(7)生成第i個優化區間,i=1,2……n,此時,Ki為以θi為中心,長度為θK的一個區間;生成優化角度序列。
(8)采用所建立的有限元模型,將模型中沖模幾何模型的錐角角度按照優化角度序列設定,進行模擬計算,獲得優化角度序列中每個角度所對應的損傷值,并生成損傷值序列D=(D1,D2,D3,D4,D5),對比損傷值序列中的損傷值,取最小的D值對應的角度,記為。
(9)在進行第i+1次優化之前,比較θK與θt的大小,如果θK≤θt,則生成并輸出下一個優化區間Ki+1作為目標區間,如果θK>θt,則繼續進行第i+1次優化,直至優化區間長度小于優化標準。
至此,利用有限元模擬的方法及設計的算法,將以θ1為中心,以θK為長度的優化區間優化為以長度小于θt的目標區間,此目標區間中包括理論上的最優錐角角度,實現了對沖模錐角的優化,獲得了優化后的錐角角度。如果需要提高優化精度,只要減小優化標準,增加優化次數便能獲得滿意的結果,而有限元模擬的使用避免了大量調模、制造模具、試生產等造成的人力物力及時間的浪費,節約成本的同時提高了效率。值得注意的是,當損傷值序列D中的最小值出現在優化區間兩端時(此時理論最優錐角角度可能不在優化區間內),仍然可以通過使用該算法進行優化區間的外擴而同時縮短優化區間長度,但是此時由于區間的減半可能出現理論最優錐角角度收斂較慢的情況,因此,需要將初始優化區間的長度盡量加大,以防止由于理論最優錐角角度不在優化區間導致的收斂較慢而影響優化效率。
本發明的有益效果是:通過建立正確的高強鋼輪輻中心孔翻邊工序的有限元模型,以損傷值作為衡量輪輻中心孔翻邊開裂幾率大小的指標,經過設定的算法,將較寬的優化區間縮小為較小的目標區間,獲得理論最優錐角角度所在的較精確的區間。從而能夠有效改進工藝設計方案并優化模具參數,提高輪輻產品質量,避免試錯法的缺陷,進而在高強鋼輪輻生產時降低生產成本和縮短產品研發周期,推動高強鋼車輪的應用和發展。
附圖說明
圖1是高強鋼輪輻中心孔翻邊沖模錐角角度優化方法流程圖;
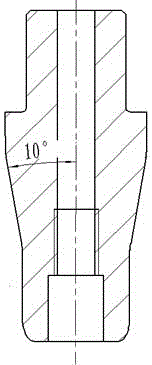
圖2是本發明實施例中所用翻邊沖模及錐角角度示意圖;
圖3是本發明實施例建立板料和成形模具幾何模型示意圖;
圖4是本發明實施例有限元模型示意圖;
圖5是本發明實施例模型動能/內能、偽應變能/內能的比值圖;
圖6是本發明實施例試驗與模擬壁厚變化率對比示意圖;
其中:1. 上模芯 2. 板料 3. 下模芯 4. 壓邊圈 5. 下模芯套。
具體實施方式
本發明是一種高強鋼輪輻中心孔翻邊沖模錐角角度優化方法。現以某公司車輪輪輻反拉深-翻邊復合成形工序為對象,梅鋼B550CL高強鋼作為輪輻材料,給出本發明的具體實施例,對反拉深-翻邊復合成形工序中的中心孔翻邊沖模錐角角度進行優化(錐角角度如圖2),參照圖1,其步驟如下:
(1)建立高強鋼輪輻中心孔翻邊成形的三維有限元模型并驗證可靠性:
本實施例選用的有限元模擬軟件為ABAQUS,首先根據反拉深-翻邊復合成形工序的板料和模具形狀尺寸,建立板料和模具的幾何模型如圖3所示(由于對稱性,建模為實際的1/4);采用單向拉伸試驗獲得高強鋼B550CL的力學性能參數,建立其板料的材料模型。為了描述材料在翻邊過程的開裂行為,本實施例選用了韓國學者YK KO等人2007年在Journal of Materials Processing Technology(材料加工技術雜志)發表的論文“Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion” (一種用于預測輪輻中心孔擴孔工序開裂的新型韌性斷裂準則)中的斷裂準則,表達式為D=,通過ABAQUS的VUMAT接口將耦合了韌性斷裂準則的本構子程序嵌入到有限元模型中;
根據實際輪輻成形工序的相關參數,將幾何模型進行裝配,完成邊界條件和摩擦的設定并對網格進行劃分,最終建立的有限元模型如圖4;
為了驗證模型可靠性,計算輪輻拉深沖孔過程中變形體動能與內能的比值以及偽應變能與內能的比值,如圖5所示。由圖可見,模擬過程中的大部分時間內動能與內能的比值較小(小于5%),因此輪輻成形過程中沒有明顯的動態效應;此外模型的偽應變能與內能的比值也很小(小于1%),說明模型的沙漏情況較輕,因此計算模型中采用的網格精度是足夠的,因此建立的有限元模型是穩定合理的;
為進一步驗證計算模型的正確性,在試驗所得輪輻和模擬結果上相同位置取16個節點,分別計算其壁厚變化率,如圖6所示。從圖中可以看出,模擬與試驗結果的壁厚變化率分布趨勢一致,最大誤差不過5%,從而說明了所建模型的準確性。
(2)根據工程設計角度和生產經驗,選定優化初始角度θ1為10°,優化區間長度θK為10°,優化標準θt為3°。
(3)生成第一個優化區間K1=[5°,15°]和第一個優化角度序列(5°,7.5°,10°,12.5°,15°)。
(4)采用所建立的有限元模型,將模型中沖模的錐角角度(如圖2所示,沖模安裝在上模芯1的對稱中心處)依次設為優化角度序列(5°,7.5°,10°,12.5°,15°),進行模擬計算,獲得優化角度序列中每個角度所對應的損傷值,生成的損傷值序列D=(1.472,1.570,1.538,1.393,1.395),可以發現最小的D值1.393對應的角度為12.5°,記為θ2;由于下一個優化區間長度θK等于5°,大于優化標準θt,所以繼續進行下一次優化。
(5)生成第二個優化區間K2=[10°,15°]和優化角度序列(10°,11.25°,12.5°,13.75°,15°)。
(6)采用所建立的有限元模型,將模型中沖模幾何模型的錐角角度按照優化角度序列設定,進行模擬計算,獲得優化角度序列中每個角度所對應的損傷值,并生成損傷值序列D=(1.538,1.418,1.393,1.360,1.395),對比損傷值序列中的損傷值,取最小的D值1.360對應的角度13.75°,記為θ3;此時下一個優化區間長度θK=2.5°小于優化標準θt,則生成并輸出K3=[12.5°,15°]作為優化目標區間。
至此,通過有限元建模和設定算法,將優化區間從[5°,15°]優化為[12.5°,15°],實現了對沖模錐角角度的優化。
以上所述,僅是本發明的實施實例,并非對本發明的技術范圍作任何限制,如果想要提高精度,可以通過縮短實施例中優化標準的長度來實現。故凡是根據本發明的技術實質對以上實例所作的任何細微修改,均屬于本發明技術方案的范圍內。
- 還沒有人留言評論。精彩留言會獲得點贊!