一種芯片內互聯線驅動器預加重功能的優化方法與流程

本發明涉及一種芯片內互聯線驅動器預加重功能的優化方法。

背景技術：

CMOS規模技術導致產生更快的設備。互連線的寬度和厚度也同樣減少了。此外，相鄰線之間的間距也變得更窄。然而，對更高級系統復雜性的需求使得芯片的平均尺寸更相近或者略大，這使得互連的長度沒有明顯減少。加長的線、交叉截面減少以及臨近互連線的周邊會產生大量寄生電阻和電容。在這樣的線路上的傳輸數字脈沖會使得延時增加和邊沿變化率變緩。這些影響特別是對高速時鐘分布和數據通信不利的。有損芯片內互連會明顯降低系統在速度和功耗方面的性能。

變換器緩沖區和中繼器因其簡單易用而廣泛應用于驅動有損線路。然而，為了增加線路的帶寬，那么要求擴大緩沖區或采用更多中繼器，這將消耗更多的能量。除電壓模式的緩沖區之外，也提出了電流模式驅動器以驅動芯片內的互聯。預加重技術是一種減少線路延時和提高信號完整性的有效方法。這種技術過度驅動，使的互連傳輸側電壓脈沖比信號擺幅高很多。實際上，通過突出驅動信號的高頻分量使得線路的低通特性均等。然而，缺少優化預加重信號波形的正式方法。

在本文中，我們提出了一種優化預加重波形的分析方法。已知互連參數和指定的互連輸出信號的擺幅和邊沿變化率，我們分析得到相應的輸入信號波形。產生的輸出信號補償線路損耗，并且產生要求的輸出信號。這個結果可用來指導互連線驅動器設計，以達到最優的速度-功率性能。

技術實現要素：

本發明要解決的技術問題是提供一種芯片內互聯線驅動器預加重功能的優化方法。

為解決上述技術問題，本發明的技術方案為：一種芯片內互聯線驅動器預加重功能的優化方法，其創新點在于：所述步驟為：

a)反向信號分析；

b)芯片內互連建模；

c)輸出電壓建模；

d)RC分布式線路；

e)RLC分布式線路。

進一步的，所述步驟a具體為：線路的特征阻抗不受控，并且線路沒有終止，驅動器將信號能量耦合到線路，接收器在線路的末端檢測輸出信號，并且與CMOS邏輯相連；

按照常規，驅動器和接收器都是基于CMOS變換器的，因此，輸入和輸出電壓都是數字脈沖，其幅度被限制為“0”和“1”兩種邏輯狀態，在本配置中，線路末端的最大的邊沿變化率是受鏈路的帶寬限制，預加重驅動器能夠克服這個缺點，并且提高互連的信號速度和完整性，在時域內，驅動器以比信號擺幅更高的電壓脈沖過度驅動線路的傳輸末端，等價地，在頻域內，驅動器通過預加重信號功率譜的高頻分量使得線路的低通特性均等化，結果，輸出信號的延時和漂移同時減少；

為了達到期望的輸出電壓的速率和電壓擺幅，需要確定過驅脈沖的數量、幅度和持續時間，過大的數值或持續時間可能導致線路末端的電壓過沖，相反地，不足的數值或持續時間導致產生信號速率沒有達到設計要求，基于所要求的輸出信號，最優輸入信號波形需要通過分析的方法來獲得；

對于電壓模式的信號，因為線路沒有終止，所以代表典型接收器的輸入阻抗，通過，輸出電流可用輸出電壓來表示；

為了從特定輸出信號反向得到輸入信號的目的，可通過傳輸矩陣來表示他們之間的關系(也被稱為ABCD矩陣)；

用式(1)代換，那么式(2)可改寫為

若ABCD元素的表達式和輸出電壓已知，那么可通過求解式(2)解析得到輸入信號。

進一步的，所述步驟b具體為：集中和分布式電路模型可被用來描述芯片內互連的行為，

RC-模型是一種低階電路，其傳輸矩陣的頻域內閉環表達式為

這里s是拉普拉斯變換的復合參數；

然而，隨著互連長度增加和信號轉換時間減少，集中模型在建模互連行為方面變得不是很準確，然后，互連需被看做是分布式系統；

對于分布式RLC模型，其頻域范圍內的傳輸矩陣的閉環表達式如下

這里是線路特征阻抗，表示如下

是傳播常數，是線路的長度

R、L和C分別為總的線路電阻、電感和電容；

結合式(3)和(5)，依據輸出電壓，輸入電壓和電流在頻域內表達如下：

因此式(8)的解都在“S”域中，逆拉普拉斯變化可用來獲得輸入電壓和電流的時域解；

然而，注意式(8)，和表達式包含cosh和sinh函數，其時域的逆拉普拉斯變換不存在，為了得到和的解析解，cosh和sinh函數可用其冪級數的泰勒展開式來替換；

用式(6)替代、式(7)替代，并且代入式(10)，那么式(8)可重寫為

式(11)中的冪級數是s的多項式的無窮和，數值計算顯示，對于R、L和C的實際值，式(11)中項的多少和信號頻率隨著n的增加而單調減少，因此，式(11)可通過只包含有限項多項式(N項和M項)來近似，高階項在誤差允許范圍內可以忽略，經過這樣的近似之后，式(11)可重新寫為

這里的系數是從式(11)得到的，并且是以線路的參數來表示

同樣地，對于，我們有

正如從式(13)和式(14)所看到，系統逆變換函數中和的值不僅依賴于線路參數，也依賴于負載阻抗，與特征阻抗相比越小，高階項在式(12)中越有意義，

N和M的值可由誤差允許所確定

這里

s＝j2πf (16)

f為信號頻率

數值例子可用來提供有價值的信息和從誤差允許方面來了解所要求的N和M值，以130-nm的CMOS過程為例，最小寬度和最小間隙的中間金屬層中1mm長互連總電阻、電感和電容分別計算為285、0.96nH和267fF，信號頻率假定為1GHz，接收端的大小假設為0.6m/0.3m；

當fF，與fF和pF時相應的誤差分別歸一化為(₀)，對于N和M的值相同時，較大的會增加數值誤差，并且因此要求式(12)S的更高階項。

進一步的，所述步驟c具體為：在數字應用中，互連輸出電壓時是數字脈沖信號，為了求解式(2)和得到互連輸入電壓和電流的解析解，、和通過閉環表達式分析建模；

分段線性模型上升沿的拉普拉斯變換的上升沿為

在式(18)中，分母中S項的最高階為2，將式(18)代入式(12)中，若N和M都不小于2的話，那么輸入信號的頻域解和中含有項，且，因此非負階項的逆拉普拉斯變換是delta函數；

L^-1[s^P]＝δ(t)，p≥0 (19)

和的時域解為和的逆拉普拉斯變換，反過來，和的時域解將包含delta函數，由于delta函數的無限功率譜密度的原因，設計一個能提供這樣的電壓或電流脈沖的互連驅動器是不可行的；

為了得到互連輸入信號的實際解，需要以其拉普拉斯變換的分母中包含足夠高階項的方式建模，頻域輸出電壓的一般表達式可重新表達為最高階為K逆多項式函數

將式(20)代入到式(12)，那么輸入信號頻域的一般表達式為

為了避免和時域解的沖擊響應，式(21)中的分母的最高階要比分子的最高階高

K＞N

K＞M. (22)

為了得到輸出電壓分母高階項的一種方法是利用拉普拉斯第n階時域微分特性，這說明函數的拉普拉斯變換等于其第n階時域微分的拉普拉斯變換除以

利用這個特性，可從的n階時域微分開始建模，而可以此積分得到

因為一階微分在時域內不連續，二階微分包含delta函數，這意味著為了完全利用式(23)顯示的特性，需為一個函數且其微分在時域內連續；

為了連續的目的，那么避免被建模為一個分段線性函數，通過sine和cosine函數來構建，其時域微分分別是sine和cosine函數，因此，所有微分也是由sine和cosine函數組成，這意味著不僅在時域連續，而且其所有的微分也是時域連續的，的連續特性意味著可用sine和cosine函數來首先設計其n階微分，然后得出和；

利用式(24)設計的優勢體現在頻域上，若的n階微分是通過sine函數建模的，那么其拉普拉斯變換是與成反比；

將式(25)代入式(23)中，分母的s項最高階為，因此，對于式(21)中的N和M，滿足條件(22)；

被假設有相等的上升和下降時間，微分包含sine函數，其時域上升沿的閉環表達式為

式(26)的拉普拉斯變換為

將式(27)代入式(23)中，是式(27)除以s的結果

在式(28)中，分母的項的最高階為3，或在式(20)中K＝3，

的上升沿表達如下

分母項的最高階為4或在式(20)中；

采用這種方法，對于任何的值，可以用式(20)來為建模，這樣的話可以得到和實際的時域波形，這個波形不包含沖擊響應。

進一步的，所述步驟d具體為：對于數字應用中大多數常規芯片內互連，線路電感沒有線路電阻和電容那么重要，為了減少計算復雜度，使用RC分布式模型，這些互連可被建模成有損傳輸線路，并且L項在式(11)中被省略，然而，因為互連是通過分布式模型來表達，那么傳輸矩陣仍然是由sinh和cosh函數所組成，同樣的微分需讓L等于0；

對于給定的互連，通過指定性能參數，例如，電壓擺幅和輸出電壓的10％–90％上升時間，可相應地得到輸入電壓和電流波形；

給定互連的規模是典型的130nm的CMOS過程，信號路徑是在最小寬度和間隙中間金屬層到周圍的接地線，此設置估計RC寄生反應的最壞情況的場景，電磁仿真計算線路電阻和電容分別為285/mm和267fF/mm，假設互連接收器是大小為0.6m/0.3m的CMOS變換器；

要求的輸出電壓上升時間為100ps，相應的輸入電壓是預加重的數字脈沖，其峰值電壓為0.07V，減少到50ps，過驅動電壓增強，其峰值等于0.29V，驅動電流脈沖的大小也增加，當進一步減少到25ps，需求明顯的預加重驅動電壓，并且其最大值為0.9V，產生這樣一個輸入波形可能不實用，因為輸入信號波形是通過反向信號分析來進行最優化，以確保互連的輸出端沒有電壓過沖，

SPICE中的正向分析被用來近似數值計算，SPICE產生實際電流脈沖以匹配分析得到輸入電流波形的一般形狀，近似電流脈沖被用來驅動互連，并且評估了所產生輸入和輸出電壓波形；

采用電流脈沖來驅動互連，所產生的互連輸入電壓有0.298V的預加重，且其1V擺幅的輸出電壓上升時間為48.5ps，結果密切匹配設計參數，雖然分析計算輸入電流波形十分復雜和不實在的，可嘗試產生電流脈沖來匹配邊沿變化率和計算電流波形的總區域，所產生的26.2ps輸出電壓上升時間和1V的擺幅接近設計規范；

通過集成瞬時功率來計算每個周期能量

保持信號擺幅會大幅增加線路上的能耗，減少輸出電壓上升時間。

進一步的，所述步驟e具體為：在現代超大規模集成電路中，芯片內互連的電感在評估互連性能方面起非常重要的作用，反向信號分析法是一種用來研究電感如何影響整個互連性能的有用工具；

RLC分布式模型參數是以RLC模型為基準，線路電阻和電容分別保持在285/mm和267fF/mm，假設信號路徑和返回路徑是最小線距的十倍，電磁仿真計算線路電感為0.96nH/mm，互連是1mm長，并且輸出電壓擺幅為1V；

SPICE中的前向分析再次用來近似反向信號分析法，通過理論分析得到的近似驅動電流信號等于49.3ps的上升時間和1-V擺幅，相應的輸入電壓有0.271V的預加重作用，當輸出電壓上升時間減少到25ps，計算輸入電流波形顯示非常復雜的方式，近似電流脈沖匹配邊沿變化率和計算電流波形的總區域，依據擺幅和上升時間，所產生的輸出電壓滿足設計規范，然而，在輸出電壓中觀察到小幅的過沖，因為近似電流脈沖不能完全取消由互連電感誘導的振鈴效應；

當輸出電壓上升時間時100ps，RC和RLC分布式模型之間的輸入電壓和電流波形非常類似，然而，當輸出電壓上升時間減少到25ps時，RLC模型的輸入電壓和電流波形顯示比RC模型更加復雜的方式，這種復雜性對于抵消由互連電感誘導的反應和振鈴效應是必要的；

對于同樣輸出電壓上升時間，互連電感可減少輸入過驅電壓的大小；

此外，輸入和輸出電壓上升時間近似滿足線性關系，輸出電壓上升時間比輸入電壓上升時間大10ps，互連電感對輸出上升時間影響最小。

本發明的優點在于：本發明的方法證明了芯片內互連驅動器預加重的優化技術，通過指定互連輸出電壓擺幅和上升時間，可分析得到驅動電壓和電流的波形，這個分析可為互連驅動器實際提供有價值的指導，仿真證明了分析得到的輸入信息的近似值能產生符合要求的輸出波形，這個分析也應用來評估互連功耗和線路電感對性能的影響。

附圖說明

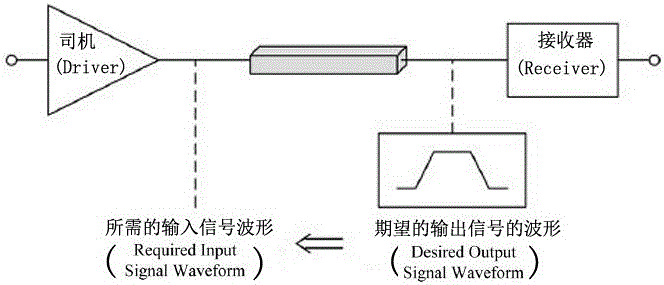
圖1顯示了芯片內互連線路的典型的發信號方法的信號分析的逆圖：通過指定波形所需的輸出信號，所需的輸入的信號波形可以據此導出。

(Fig.1.Illustration of the inverse signaling analysis：by specifying the waveform of the desired output signal，the required input signal waveform can be derived accordingly)。

圖2為圖1中的互連可建模成的兩端網絡圖：圖2中二端口網絡模型的芯片信號，其中Z_L表示負載阻抗的線

Fig.2.Two-port network model of the on-chip signaling，where Z_Lrepresents(the load impedance of the line.)。

圖3顯示集中RC-模型，這是一種為互連的信號延時建模的簡單方法結構示意圖

Fig.3.Lumped RCπ-model of on-chip interconnects，where R_w andC_w are(the total interconnect resistance and capacitance，respectively.)。

圖4顯示RLC互連的分布式電路模型的結構示意圖：圖4分布式的RLC模型上的片上互連線作為有損傳輸線，R、L和C分別是線電阻、電感和電容單位長度

Fig.4shows the distributed circuit model of RLC intercon-nects，where R，L，and C are per-unit-length interconnect resis-(tance，inductance，and capacitance，respectively.)。

圖5分別畫出了數值誤差和反N和M的曲線圖

(Fig.5.Numerical errors of(12)against N and M.)。

圖6為比較了互連的不同負載電容時的平均數值誤差的曲線圖：

對N到M的數值誤差(ε>的意思是：<ε>在尊重C_L＝100fF and C_L＝1pF，分別被規范化為<ε>當C_L＝10fF

Fig.6.Mean numerical errors<ε>against N and M.<ε>in respect to C_L＝(100fF and C_L＝1pF，respectively，are normalized to<ε>when C_L＝10fF.)。

圖7顯示了時域數字脈沖的常規分段模型示意圖

Fig.7.Piecewise linear model of the interconnect output voltage in time do-(main，where V₀is the signal swing and t_r is the 10％-90％rise time.)。

圖8顯示圖7中分段線性模型的一階和二階時域微分

Fig.8.(a)First-and(b)second-order derivatives of the piecewise linear model(of a digital pulse.)。

圖9(a)顯示從其一階微分得出的的波形曲線圖。

圖9(b)顯示了從的二階微分得出的波形。

Fig.9.Design examples of deriving the output voltage waveform from its nth-order derivatives.The voltage scale is normalized to the signal swing V₀(and the time scale is normalized to the 10％～90％rise time t_r.)。

圖10為給定互連的規模是典型的130nm的CMOS過程曲線圖

Fig.10.Cross section of an on-chip interconnect on an intermediate metal layer(with minimum width and spacing to surrounding ground lines.)。

圖11(a)(b)(c)所示的數值結果也被用來計算線路上能耗與輸出電壓上升時間的曲線圖

Fig.11.Design examples for the RC distributed line.The input voltage and current waveforms for 1-mm-long line with output voltage rise time of(a)100，((b)50，and(c)25ps，respectively.)。

圖12(a)(b)顯示輸出電壓50s上升時間的近似過程的曲線圖

(Fig.12.SPICE approximation of the inverse signaling analysis.The interconnect is a1-mm-long_distributed line.The design parameters for the interconnect output voltage are 1-V signal swing，and 10％-90％rise time of(a)50and(b)25ps，respectively)。

圖13為計算線路上能耗與輸出電壓上升時間的曲線圖

(Fig.13.Energy consumption per cycle versus the output voltage rise time)。

圖14顯示對于驅動RLC分布式模型分別達到100、50和25ps上升時間的10％–90％時，設計輸入電壓和電流波形的數值例子的曲線圖

(Fig.14.Design examples for RLC distributed line.Input voltage and current waveforms for 1-mm-long line with output voltage rise time of(a)100,(b)50,and(c)25ps,respectively)。

在圖15(a)(b)顯示了期望的輸出電壓與上升時間的曲線圖

(Fig.15.SPICE approximation of the inverse signaling analysis.The interconnect is a 1-mm-long RLC distributed line.The design parameters for the interconnect output voltage are 1-V signal swing,and 10％–90％rise time of(a)50and(b)25ps,respectively)。

圖16顯示了最大過驅電壓的大小與輸出電壓上升時間的關系圖

(Fig.16.Maximum input overdrive voltage versus output voltage rise time for different values of the line inductance)。

圖17顯示了輸入電壓上升時間與輸出電壓上升時間的曲線圖

(Fig.17.Interconnect input voltage 10％–90％rise time versus output voltage rise time for different values of line inductance)。

具體實施方式

本發明的芯片內互聯線驅動器預加重功能的優化方法通過以下步驟實現：

第一步，反向信號分析：

圖1顯示了芯片內互連線路的典型的發信號方法。線路的特征阻抗不受控，并且線路沒有終止。驅動器將信號能量耦合到線路。接收器在線路的末端檢測輸出信號，并且與CMOS邏輯相連。

按照常規，驅動器和接收器都是基于CMOS變換器的。因此，輸入和輸出電壓都是數字脈沖，其幅度被限制為“0”和“1”兩種邏輯狀態。在本配置中，線路末端的最大的邊沿變化率是受鏈路的帶寬限制。預加重驅動器能夠克服這個缺點，并且提高互連的信號速度和完整性。在時域內，驅動器以比信號擺幅更高的電壓脈沖過度驅動線路的傳輸末端。等價地，在頻域內，驅動器通過預加重信號功率譜的高頻分量使得線路的低通特性均等化。結果，輸出信號的延時和漂移同時減少。

為了達到期望的輸出電壓的速率和電壓擺幅，需要確定過驅脈沖的數量、幅度和持續時間。過大的數值或持續時間可能導致線路末端的電壓過沖。相反地，不足的數值或持續時間導致產生信號速率沒有達到設計要求。基于所要求的輸出信號，最優輸入信號波形需要通過分析的方法來獲得。

圖1中的互連可建模成一個如圖2所示的兩端網絡。這里是驅動器提供的驅動電壓，為接收器的輸入口的輸出電壓，是互連的負載阻抗。

對于電壓模式的信號，因為線路沒有終止，所以代表典型接收器的輸入阻抗。通過，輸出電流可用輸出電壓來表示。

為了從特定輸出信號反向得到輸入信號的目的，可通過傳輸矩陣來表示他們之間的關系(也被稱為ABCD矩陣)。

用式(1)代換，那么式(2)可改寫為

若ABCD元素的表達式和輸出電壓已知，那么可通過求解式(2)解析得到輸入信號。

第二步，芯片內互連建模：

集中和分布式電路模型可被用來描述芯片內互連的行為。圖3顯示集中RC-模型，這是一種為互連的信號延時建模的簡單方法，和分別是總的互連電阻和電容。

RC-模型是一種低階電路，其傳輸矩陣的頻域內閉環表達式為

這里s是拉普拉斯變換的復合參數。

然而，隨著互連長度增加和信號轉換時間減少，集中模型在建模互連行為方面變得不是很準確。然后，互連需被看做是分布式系統。

圖4顯示RLC互連的分布式電路模型，這里R、L和C分別是每單位長度互連的電阻、電感和電容。

對于分布式RLC模型，其頻域范圍內的傳輸矩陣的閉環表達式如文獻所示。

這里是線路特征阻抗，表示如下

是傳播常數，是線路的長度

R、L和C分別為總的線路電阻、電感和電容。

結合式(3)和(5)，依據輸出電壓，輸入電壓和電流在頻域內表達如下：

因此式(8)的解都在“S”域中，逆拉普拉斯變化可用來獲得輸入電壓和電流的時域解。

然而，注意式(8)，和表達式包含cosh和sinh函數，其時域的逆拉普拉斯變換不存在。為了得到和的解析解，cosh和sinh函數可用其冪級數的泰勒展開式來替換。

用式(6)替代、式(7)替代，并且代入式(10)，那么式(8)可重寫為

式(11)中的冪級數是s的多項式的無窮和。數值計算顯示，對于R、L和C的實際值，式(11)中項的多少和信號頻率隨著n的增加而單調減少。因此，式(11)可通過只包含有限項多項式(N項和M項)來近似。高階項在誤差允許范圍內可以忽略。經過這樣的近似之后，式(11)可重新寫為

這里的系數是從式(11)得到的，并且是以線路的參數來表示

同樣地，對于，我們有

正如從式(13)和式(14)所看到，系統逆變換函數中和的值不僅依賴于線路參數，也依賴于負載阻抗。與特征阻抗相比越小，高階項在式(12)中越有意義。

N和M的值可由誤差允許所確定

這里

s＝j2πf (16)

f為信號頻率

數值例子可用來提供有價值的信息和從誤差允許方面來了解所要求的N和M值。以130-nm的CMOS過程為例，最小寬度和最小間隙的中間金屬層中1mm長互連總電阻、電感和電容分別計算為285、0.96nH和267fF。信號頻率假定為1GHz。接收端的大小假設為0.6m/0.3m。

圖5分別畫出了數值誤差和反_N和_M。從圖5中可以看到數值計算誤差隨著N和M明顯下降。因此，選擇較大的N和M值不應明顯影響數值精度。

圖6比較了互連的不同負載電容時的平均數值誤差()，()定義為N和_M的平均值，

在圖中，當fF，與fF和pF時相應的誤差分別歸一化為(₀)。對于N和M的值相同時，較大的會增加數值誤差，并且因此要求式(12)S的更高階項。

第三步，輸出電壓建模：

在數字應用中，互連輸出電壓時是數字脈沖信號。為了求解式(2)和得到互連輸入電壓和電流的解析解，、和通過閉環表達式分析建模。

圖7顯示了時域數字脈沖的常規分段模型，這里信號上升沿和下降沿都是線性的，電壓擺幅是，信號從10％-90％的時間為。圖7中分段線性模型上升沿的拉普拉斯變換的上升沿為

在式(18)中，分母中S項的最高階為2。將式(18)代入式(12)中，若N和M都不小于2的話，那么輸入信號的頻域解和中含有項，且。因此非負階項的逆拉普拉斯變換是delta函數。

L^-1[s^P]＝δ(t)，p≥0 (19)

和的時域解為和的逆拉普拉斯變換，反過來，和的時域解將包含delta函數。由于delta函數的無限功率譜密度的原因，設計一個能提供這樣的電壓或電流脈沖的互連驅動器是不可行的。

為了得到互連輸入信號的實際解，需要以其拉普拉斯變換的分母中包含足夠高階項的方式建模。頻域輸出電壓的一般表達式可重新表達為最高階為K逆多項式函數

將式(20)代入到式(12)，那么輸入信號頻域的一般表達式為

為了避免和時域解的沖擊響應，式(21)中的分母的最高階要比分子的最高階高

K＞N

K＞M. (22)

為了得到輸出電壓分母高階項的一種方法是利用拉普拉斯第n階時域微分特性，這說明函數的拉普拉斯變換等于其第n階時域微分的拉普拉斯變換除以

利用這個特性，可從的n階時域微分開始建模，而可以此積分得到

圖8顯示圖7中分段線性模型的一階和二階時域微分。因為一階微分在時域內不連續，二階微分包含delta函數。這意味著為了完全利用式(23)顯示的特性，需為一個函數且其微分在時域內連續。

為了連續的目的，那么避免被建模為一個分段線性函數，通過sine和cosine函數來構建，其時域微分分別是sine和cosine函數。因此，所有微分也是由sine和cosine函數組成。這意味著不僅在時域連續，而且其所有的微分也是時域連續的。的連續特性意味著可用sine和cosine函數來首先設計其n階微分，然后得出和。

利用式(24)設計的優勢體現在頻域上。若的n階微分是通過sine函數建模的，那么其拉普拉斯變換是與成反比。

將式(25)代入式(23)中，分母的s項最高階為。因此，對于式(21)中的N和M，滿足條件(22)。

圖9顯示如何使用sine函數建模及其微分的兩個例子。設計參數是信號擺幅和從10％-90％的上升時間。注意在這些圖中，時間范圍歸一化為，并且電壓范圍歸一化為。

圖9(a)顯示從其一階微分得出的的波形。被假設有相等的上升和下降時間(雖然非必要)。微分包含sine函數，其時域上升沿的閉環表達式為

式(26)的拉普拉斯變換為

將式(27)代入式(23)中，是式(27)除以s的結果

在式(28)中，分母的項的最高階為3，或在式(20)中K＝3。

類似地，圖9(b)顯示了從的二階微分得出的波形。的上升沿表達如下

在本例中，分母項的最高階為4或在式(20)中。

比較圖9(a)和圖9(b)，雖然的頻域表達式是大不相同的，的設計參數依然相同，并且信號上升沿的形狀的差別非常微小。

采用這種方法，對于任何的值，可以用式(20)來為建模，這樣的話可以得到和實際的時域波形，這個波形不包含沖擊響應。

第四步，RC分布式線路：

對于數字應用中大多數常規芯片內互連，線路電感沒有線路電阻和電容那么重要。為了減少計算復雜度，使用RC分布式模型，這些互連可被建模成有損傳輸線路，并且L項在式(11)中被省略。然而，因為互連是通過分布式模型來表達，那么傳輸矩陣仍然是由sinh和cosh函數所組成。同樣的微分需像在第三部分和第四部分給出的那樣，讓L等于0。

本部分顯示了在RC分布式線路上應用反向信號分析的數值例子。對于給定的互連，通過指定性能參數，例如，電壓擺幅和輸出電壓的10％–90％上升時間，可相應地得到輸入電壓和電流波形。

給定互連的規模是典型的130nm的CMOS過程，其交叉部分如圖10所示。信號路徑是在最小寬度和間隙中間金屬層到周圍的接地線。此設置估計RC寄生反應的最壞情況的場景。電磁仿真計算線路電阻和電容分別為285/mm和267fF/mm。假設互連接收器是大小為0.6m/0.3m的CMOS變換器。

圖11證明了1mm長互連的情況，這里假設輸出信號的信號擺幅為1V。每個子圖表示不同的輸出電壓上升時間值，并且顯示驅動電壓和電流的相應的時域波形。

在圖11(a)中，要求的輸出電壓上升時間為100ps。相應的輸入電壓是預加重的數字脈沖，其峰值電壓為0.07V。在圖11(b)中，減少到50ps，過驅動電壓增強，其峰值等于0.29V。驅動電流脈沖的大小也增加。在圖11(c)中，當進一步減少到25ps，需求明顯的預加重驅動電壓，并且其最大值為0.9V。產生這樣一個輸入波形可能不實用。因為輸入信號波形是通過反向信號分析來進行最優化，以確保互連的輸出端沒有電壓過沖。

SPICE中的正向分析被用來近似數值計算。SPICE產生實際電流脈沖以匹配分析得到輸入電流波形的一般形狀。近似電流脈沖被用來驅動互連，并且評估了所產生輸入和輸出電壓波形。

圖12(a)顯示輸出電壓50s上升時間的近似過程。在SPICE，電流脈沖近似匹配圖12(a)中輸入電流的形狀。采用這個電流脈沖來驅動互連，所產生的互連輸入電壓有0.298V的預加重，且其1V擺幅的輸出電壓上升時間為48.5ps。結果密切匹配設計參數。圖12(b)顯示互連輸出的25ps上升時間的例子。雖然分析計算輸入電流波形十分復雜和不實在的，可嘗試產生電流脈沖來匹配邊沿變化率和計算電流波形的總區域。所產生的26.2ps輸出電壓上升時間和1V的擺幅接近設計規范。

前面提到的SPICE仿真顯示給定性能參數，反向信號分析可為設計互連驅動信號提供有價值的指導。即使在計算輸入波形太復雜而無法實現的地方，近似信號波形幾乎符合設計規范。

以前，文獻依據其輸入轉換相關的能耗為RC樹網絡建模。如圖13所示的數值結果也被用來計算線路上能耗與輸出電壓上升時間。通過集成這個時期的瞬時功率來計算每個周期能量

從圖可知，保持信號擺幅會大幅增加線路上的能耗，減少輸出電壓上升時間。

第五步，RLC分布式線路：

在現代超大規模集成電路(VLSI)中，芯片內互連的電感在評估互連性能方面起非常重要的作用。反向信號分析法是一種用來研究電感如何影響整個互連性能的有用工具。

RLC分布式模型參數是以RLC模型為基準。線路電阻和電容分別保持在285/mm和267fF/mm。假設信號路徑和返回路徑是最小線距的十倍。電磁仿真計算線路電感為0.96nH/mm。互連是1mm長，并且輸出電壓擺幅為1V。圖13顯示對于驅動RLC分布式模型分別達到100、50和25ps上升時間的10％–90％時，設計輸入電壓和電流波形的數值例子。

SPICE中的前向分析再次用來近似反向信號分析法。在圖15(a)，期望的輸出電壓擺幅為1V，10％–90％上升時間為50ps。通過理論分析得到的近似驅動電流信號等于49.3ps的上升時間和1-V擺幅。相應的輸入電壓有0.271V的預加重作用。在圖15(b)中，當輸出電壓上升時間減少到25ps，計算輸入電流波形顯示非常復雜的方式。近似電流脈沖匹配邊沿變化率和計算電流波形的總區域。依據擺幅和上升時間，所產生的輸出電壓滿足設計規范。然而，在輸出電壓中觀察到小幅的過沖，因為近似電流脈沖不能完全取消由互連電感誘導的振鈴效應。

通過比較圖11和圖14，可以看出互連電感的影響。當輸出電壓上升時間時100ps，RC和RLC分布式模型之間的輸入電壓和電流波形非常類似。然而，當輸出電壓上升時間減少到25ps時，RLC模型的輸入電壓和電流波形顯示比RC模型更加復雜的方式。這種復雜性對于抵消由互連電感誘導的反應和振鈴效應是必要的。

圖14的仔細檢查揭示了RLC模型的過驅電壓比RC模型的小。為了量化這種影響，最大過驅電壓的大小與輸出電壓上升時間的關系如圖16所示。從圖可得出對于同樣輸出電壓上升時間，互連電感可減少輸入過驅電壓的大小。

此外，輸入電壓上升時間與輸出電壓上升時間如圖17所示。圖中的三條曲線表示不同的互連電感值。可以看到輸入和輸出電壓上升時間近似滿足線性關系，輸出電壓上升時間比輸入電壓上升時間大10ps。互連電感對輸出上升時間影響最小。

以上顯示和描述了本發明的基本原理和主要特征和本發明的優點。本行業的技術人員應該了解，本發明不受上述實施例的限制，上述實施例和說明書中描述的只是說明本發明的原理，在不脫離本發明精神和范圍的前提下，本發明還會有各種變化和改進，這些變化和改進都落入要求保護的本發明范圍內。本發明要求保護范圍由所附的權利要求書及其等效物界定。