基于局部加權貝葉斯網絡的自適應軟測量預測方法與流程

本發明屬于工業過程控制領域，尤其涉及一種基于局部加權貝葉斯網絡的自適應軟測量預測方法。
背景技術：
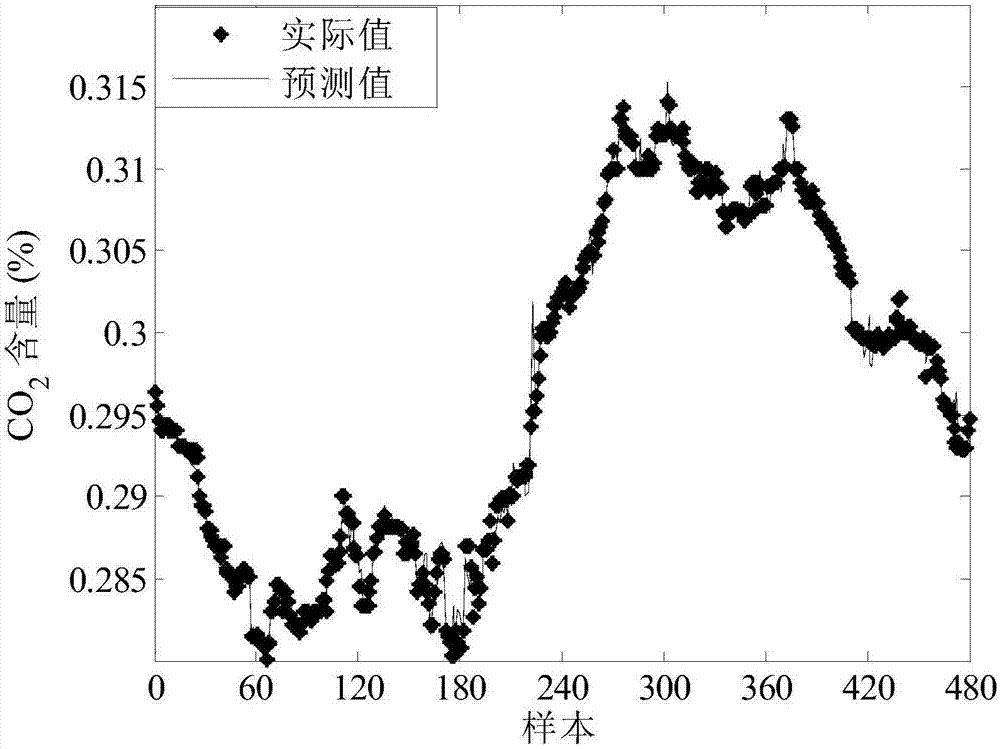
：軟測量的目標是建立適當的模型，使用易于測量的過程變量預測難以測量或者測量存在大時延的質量變量。實時準確的預測出質量變量有利于控制產品質量，提高生產效率。軟測量模型一般分為機理模型和數據驅動的模型。隨著計算機技術的發展，數據驅動的建模方法受到了越來越多的關注。常見的數據驅動建模方法有很多，目前使用最廣泛的是主成分分析和偏最小二乘方法，這兩種都是線性模型；考慮到過程的不確定性，將概率形式加入到這兩種方法中，就得到了概率的主成分分析和基于概率的偏最小二乘方法；如果工業過程呈現出多個模態，高斯混合模型可以很好地處理這一難題；將支持向量回歸的思想用于軟測量領域也可取得較高的預測精度；還有神經網絡的方法也可用于質量預測。但在實際工業過程中，由于過程的漂移、催化劑的失效等會引起模型的退化，簡單地說就是原來建立的模型不再適用于現有的運行狀態。為了解決這一問題，出現了不少自適應的方法。即時學習是眾多自適應軟測量方法中的一種，而局部加權的方法又是即時學習中最重要的一種。貝葉斯網絡是一種概率圖論模型，它在處理不確定性問題中有很大的優勢。技術實現要素：針對現有技術中的不足，本發明提出一種基于局部加權貝葉斯網絡的自適應軟測量預測方法，其能在工業過程存在漂移的情況下，也能較準確地給出質量預報，即使在訓練數據和測試數據均存在不同程度缺失的情況下，也能獲得較高的預測精度。具體技術方案如下：一種基于局部加權貝葉斯網絡的自適應軟測量預測方法，包括以下步驟：步驟一：收集工業過程中的歷史數據集：將易于測量的過程變量作為輸入，即x＝[x1；x2；…；xn]∈rn×m，其中x的每一列代表一個過程變量，每一行代表一個樣本；將不容易實時測量的質量變量作為輸出，即y＝[y1；y2；…yn]∈rn×1；步驟二：從歷史數據集中選擇建立貝葉斯網絡模型的樣本，具體如下：(a)新來一個輸入樣本xq，選擇與該樣本最相近的k個樣本，即計算歷史數據中的第n個輸入樣本xn與xq的歐式距離dn，并對計算出的歐式距離進行排序，選出歐式距離最小的k個樣本，其中歐式距離的計算公式如下：(b)計算(a)中挑選出的k個樣本的權重，計算公式如下：其中，表示位置參數，通常在0-1之間取值；σd表示公式(1)中求得歐式距離的標準差。(c)獲得訓練數據：將(a)中選出的k個樣本分別乘以公式(2)計算得到的各自的權重，作為局部加權處理后的訓練數據，公式如下：(d)計算(c)中處理后訓練數據輸入、輸出的均值按如下方式計算：步驟三：用選出的k個樣本建立貝葉斯網絡，得到預測結果，具體如下：(a)對數據進行標準化處理：用步驟二得到的輸入輸出均值分別對步驟二中得到的作標準化化處理；(b)根據專家知識，將所有輸入變量作為貝葉斯網絡的父節點，待預測的輸出變量作為子節點，各父節點與子節點間用一根帶箭頭的線連接，箭頭指向子節點，各父節點間沒有線直接相連，從而得到貝葉斯網絡的結構；(c)當各節點服從高斯分布時，將所有父節點設置為可觀測節點，唯一的子節點設置為隱含節點，將(a)中的標準化后數據放入貝葉斯網絡中進行參數學習，如果此時的建模樣本中存在數據缺失現象，將缺失值置為空后，直接進行后面的參數學習；所述的參數學習過程采用em算法，通過不斷迭代給出各個節點參數的最大似然估計；當數據中存在缺失現象時，參數學習的過程大致如下：隨機給定缺失數據的初值，根據給定初值估計模型參數；根據估計的模型參數重新計算缺失值，如此反復迭代直至待估計參數收斂；(d)根據上步參數學習的結果，獲得步驟(b)中各節點的先驗概率分布，包括各節點的均值和方差，此時得到一個完整的貝葉斯網絡；(e)將待預測的輸入樣本xq去中心化處理后，作為證據添加進(d)中建立的完整的貝葉斯網絡中，通過聯合樹推理引擎獲得待預測節點的后驗概率分布，包括輸出的均值和方差；將均值作為預測值，并計算實際測量真值y與預測值yq的誤差；步驟四：一旦完成預測后，當前模型被丟棄，當下一個新樣本x′q到來時，重復步驟二和三，建立新的貝葉斯網絡模型，得到y′q的預測值和預測誤差。進一步地，所述的方差采用均方根誤差rmse衡量預測結果的準確性，其計算公式如下：公式中n表示測試樣本的個數，yreal代表測量的真實值，ypred代表由貝葉斯網絡得到的預測值。本發明的有益效果是：本發明提出的基于局部加權貝葉斯網絡的方法，每新來一個待預測樣本，從歷史數據中選擇與它最相近的樣本建立貝葉斯網絡，完成預測后，該局部模型立即被丟棄。本發明的優勢在于，在工業過程存在漂移的情況下，也能較準確地給出質量預報，即使在訓練數據和測試數據均存在不同程度缺失的情況下，也能獲得較高的預測精度。附圖說明圖1為本發明方法預測co2剩余含量的結果示意圖；圖2為局部加權的偏最小二乘方法預測co2剩余含量的結果示意圖；圖3為本發明方法在訓練數據約有15％缺失的情況下的結果示意圖。具體實施方式本發明針對工業過程中的軟測量問題，該方法首先從歷史數據集中選出與待預測樣本最接近的數據作訓練樣本，運用貝葉斯網絡的方法建立模型，并將待預測樣本的輸入作為證據添加進網絡中，經推理得出預測值。一旦完成預測后，該模型立即被丟棄，當下一個待預測樣本到來時，重新建立局部模型。下面結合具體的實施例對本發明的基于局部加權貝葉斯網絡的自適應軟測量預測方法作進一步的說明。一種基于局部加權貝葉斯網絡的自適應軟測量預測方法，包括以下步驟：步驟一：收集工業過程中的歷史數據集：將易于測量的過程變量作為輸入，即x＝[x1；x2；…；xn]∈rn×m，其中x的每一列代表一個過程變量，每一行代表一個樣本；將不容易實時測量的質量變量作為輸出，即y＝[y1；y2；…yn]∈rn×1；步驟二：從歷史數據集中選擇建立貝葉斯網絡模型的樣本，具體如下：(a)新來一個輸入樣本xq，選擇與該樣本最相近的k個樣本，即計算歷史數據中的第n個輸入樣本xn與xq的歐式距離dn，并對計算出的歐式距離進行排序，選出歐式距離最小的k個樣本，其中歐式距離的計算公式如下：(b)計算(a)中挑選出的k個樣本的權重，計算公式如下：其中，表示位置參數，通常在0-1之間取值；σd表示公式(1)中求得歐式距離的標準差。(c)獲得訓練數據：將(a)中選出的k個樣本分別乘以公式(2)計算得到的各自的權重，作為局部加權處理后的訓練數據，公式如下：(d)計算(c)中處理后訓練數據輸入、輸出的均值，按如下方式計算：步驟三：用選出的k個樣本建立貝葉斯網絡，得到預測結果，具體如下：(a)對數據進行標準化處理：用步驟二得到的輸入輸出均值分別對步驟二中得到的作標準化處理；(b)根據專家知識，將所有輸入變量作為貝葉斯網絡的父節點，待預測的輸出變量作為子節點，各父節點與子節點間用一根帶箭頭的線連接，箭頭指向子節點，各父節點間沒有線直接相連，從而得到貝葉斯網絡的結構；(c)當各節點服從高斯分布時，將所有父節點設置為可觀測節點，唯一的子節點設置為隱含節點，將(a)中的標準化后數據放入貝葉斯網絡中進行參數學習，如果此時的建模樣本中存在數據缺失現象，將缺失值置為空后，直接進行后面的參數學習；所述的參數學習過程采用em算法，通過不斷迭代給出各個節點參數的最大似然估計；當數據中存在缺失現象時，參數學習的過程大致如下：隨機給定缺失數據的初值，根據給定初值估計模型參數；根據估計的模型參數重新計算缺失值，如此反復迭代直至待估計參數收斂；(d)根據上步參數學習的結果，獲得步驟(b)中各節點的先驗概率分布，包括各節點的均值和方差，此時得到一個完整的貝葉斯網絡；(e)將待預測的輸入樣本xq去中心化處理后，作為證據添加進(d)中建立的完整的貝葉斯網絡中，通過聯合樹推理引擎獲得待預測節點的后驗概率分布，包括輸出的均值和方差；將均值作為預測值，并計算實際測量真值y與預測值yq的誤差；所述的方差采用均方根誤差rmse衡量預測結果的準確性，其計算公式如下：公式中n表示測試樣本的個數，yreal代表測量的真實值，ypred代表由貝葉斯網絡得到的預測值。顯然，均方根誤差rmse越小，表示貝葉斯網絡預測的精度越高。用該指標可以定量比較各種模型的預測能力。步驟四：一旦完成預測后，當前模型被丟棄，當下一個新樣本x′q到來時，重復步驟二和三，建立新的貝葉斯網絡模型，得到y′q的預測值和預測誤差。以下結合一個具體的工業過程的例子來說明本發明的有效性。co2吸收塔是實際化工合成氨過程中的一個子單元。整個工藝過程可大致描述為：來自前一單元的工藝氣經過初步降溫后，在工藝冷凝分離罐再次降溫，進入吸收塔。經過吸收塔后的工藝氣，送入到除霧分離罐中，殘余co2由儀表記錄。罐中吸收co2后，吸收液由貧液，半貧液變成富液。富液從罐底部經富液閃蒸槽送入再生塔中，進行溶液的再生操作，再生的溶液被抽回吸收塔。co2吸收塔中發生的主要化學反應是co2+k2co3+h2o←→2khco3+q。為了最大限度地利用co2，最后工藝氣中殘余的co2含量應盡可能的少。吸收塔中共有12個變量如下表1給出。前11個變量較易測量得到，第12個變量工藝氣中殘余co2含量較難測量，因此對這12個變量建立貝葉斯網絡，用前11個變量預測co2剩余含量。接下來結合該具體過程對本發明的實施步驟進行詳細地闡述：表1co2吸收塔工藝中的變量變量編號變量描述1工藝氣壓力12液位13出口貧液溫度4貧液流量5半貧液流量6出口工藝氣溫度7工藝氣進出口壓差8出口富液溫度9液位210高液位報警值11工藝氣壓力212工藝氣中殘余co2含量采集co2吸收塔正常運行過程中的數據，對于待預測的輸入樣本xq，在歷史數據中選擇與它最相近的k個樣本，對挑選出的樣本作加權處理后用于后續建立貝葉斯網絡。根據專家知識，確定貝葉斯網絡的結構：共有12個節點，前11個為可觀測的父節點，第12個節點為隱含的子節點，共有12條有向邊，均為從父節點出發指向同一個子節點。當這12個節點均服從高斯分布時，用步驟1加權處理后的k個樣本進行參數學習，獲得這12個節點的先驗概率分布。將新來樣本的輸入xq作為證據添加進已建好的貝葉斯網絡中，由聯合樹推理引擎求得唯一子節點的后驗概率分布，即子節點的均值和方差。將求得的均值作為預測值，方差反映了預測值的波動大小，可作為預測值精度的衡量指標。預測完成后，該局部模型立即被丟棄，當下一個新樣本x′q到來時，重新建立新的貝葉斯網絡。一旦獲得待預測量的真值后，計算預測誤差。采用本發明方法預測co2剩余含量的結果如圖1所示，局部加權的偏最小二乘方法預測co2剩余含量的結果如圖2所示，兩種方法的預測精度對比如表2所示，從表2可以看出，本發明的基于局部加權的貝葉斯網絡的預測方法比局部加權的偏最小二乘方法的預測精度高。表2本發明方法和局部加權的偏最小二乘方法的預測精度對比表建模方法預測的均方根誤差預測最大誤差的絕對值局部加權的貝葉斯網絡0.00060720.002356局部加權的偏最小二乘0.00097350.007976本發明方法在數據約有15％缺失的情況下的預測結果如圖3所示，從圖3中可以看出，即使在數據存在一定缺失率的情況下，本發明仍然有較高的預測精度。上述實施例用來解釋說明本發明，而不是對本發明進行限制，在本發明的精神和權利要求的保護范圍內，對本發明做出的任何修改和改變，都落入本發明的保護范圍。當前第1頁12