一種基于Tau理論的航天器交會制導方法與流程

本發明屬于航天動力學領域，具體涉及一種基于tau理論的航天器交會制導方法。

背景技術：

在開啟空間探索活動的短短幾十年間，人類已經將數千枚人造衛星送入太空，用于執行各種各樣的空間任務。從之前的發展趨勢來看，二十一世紀將是人類在空間領域取得重大突破和取得飛速發展的世紀。在這種形勢下，對空間資源的開發和利用越來越離不開天地物資與人員的往返能力，離不開航天器之間的物質與能量轉移。上述這些活動的開展都緊緊地依賴于一項關鍵技術的發展------交會對接技術，該技術已經成為了保證國家空間技術優勢的重要組成部分。作為未來空間領域的常規性任務之一，空間交會對接技術的研究與發展受到了各航天大國的重視。空間交會對接技術已經成為一種勢能技術，對于該技術的研究與發展具有很大的緊迫性和前沿性。

在過去的幾十年間，已經有很多學者對空間交會對接技術進行了廣泛的研究，并取得了一些代表性的成果。之前很多的研究都是針對脈沖推力作用下的航天器交會任務，包括被廣泛提及的v_bar方法、r_bar方法以及滑移制導律方法。這些方法大多都是基于cw線性相對運動方程發展而來的，認為瞬時脈沖是可以任意獲得，并且沒有考慮外界的干擾力影響。后來，很多學者又提出了很多的基于連續推力的交會方法，例如基于最優控制理論的航天器交會制導方法、基于逆動力學理論的航天器交會制導方法等等。這些方法雖然可以設計出一條滿足要求的交會軌跡，但是普遍存在計算量大的問題，不適于實時在線計算的要求。針對上述研究中存在的問題，本發明提出了一種基于tau理論的航天交會制導方法。tau理論是認知科學研究者通過試驗總結出的人和動物在接近和抓取物體時的運動策略。tau認為人或動物為了完成接觸或抓取操作而接近某一個物體時，會很自然地利用視線線索提供的預測時間信息來導引和調節自己的工作。tau理論是一種仿生學的理論，它是動物們在經歷自然變遷與物種進化后保留下來的本領，因此tau理論本身就具有很強的適應性并具有一定的最優性。

技術實現要素：

本發明所要解決的技術問題在于針對上述現有技術中的不足，提出了一種基于tau理論的交會制導方法，利用該方法可以設計得到一條合適交會軌跡，并通過數值仿真進行了驗證。

本發明采用以下技術方案：

一種基于tau理論的航天器交會制導方法，包括以下步驟：

s1、建立航天器近距離交會過程中的相對動力學方程，利用tau理論對交跟蹤航天器接近過程中的交會軌跡進行設計；

s2、根據步驟s1所述交會軌跡求解交會過程中所需的交會速度和交會加速度；

s3、分析不同的tau-g耦合因子對于所述交會軌跡的影響，調整tau-g耦合因子最終確定tau-g耦合因子的合理取值區間；

s4、利用逆動力學方法求解所述交會軌跡中跟蹤航天器施加的控制加速度。

優選的，步驟s1中，基于tau理論的所述交會軌跡表示為：

其中，r(tg)＝[x(tg)；y(tg)；z(tg)]表示交會終端時刻的相對位置，r0＝[x(0)；y(0)；z(0)]表示交會初始時刻的相對位置，tg表示交會過程所持續的時間，kg表示tau_g耦合因子。

優選的，步驟s1中，所述交會軌跡分解為三個坐標分量為：

其中，tg為交會過程所持續的時間，kg為tau_g耦合因子，t為時間變量。

優選的，所述交會速度為：

其中，tg為交會過程所持續的時間，kg為tau_g耦合因子，t為時間變量。

優選的，所述交會加速度為：

其中，tg為交會過程所持續的時間，kg為tau_g耦合因子，t為時間變量。

優選的，所述相對動力學方程具體為：

其中，[x；y；z]表示跟蹤航天器相對于目標航天器的位置在目標航天器軌道坐標系中的分量，n表示目標航天器的軌跡角速率，[fx；fy；fz]表示跟蹤航天器所施加的控制加速度在目標航天器軌道系中的分量。

優選的，所述交會軌跡中跟蹤航天器施加的控制加速度為：

其中，[fzn；fzn；fzn]表示生成交會軌跡所需要的控制加速度，tg為交會過程所持續的時間，kg為tau_g耦合因子，t為時間變量。

優選的，步驟s3中，通過所述交會軌跡的二階導數對應輸入控制力，確定耦合因子kg的選擇范圍為0～0.5。

與現有技術相比，本發明至少具有以下有益效果：

本發明首先對近距離交會過程中的相對運動模型進行分析，然后基于tau理論給出了交會軌跡的表達形式，然后通過對交會軌跡求導進而得到了交會過程中所需的速度，利用逆動力學方法對交會過程中所需的控制加速度進行了求解，基于tau理論的交會方法是一種解析的方法，能夠給出交會軌跡、交會速度以及所需控制力的解析表達式，因此可以減小星載計算機的運算負擔，同時該理論是一種基于仿生學的理論，能夠使得所設計的交會軌跡具有很強的環境適應性。

進一步的，本發明采用一種仿生學方法，它是對自然界的動物在經過成千上萬年不斷優化所形成的本能運動的歸納和總結，利用本方法所設計的交會軌跡不僅能夠滿足交會要求，而且具備很好的適應性。

下面通過附圖和實施例，對本發明的技術方案做進一步的詳細描述。

附圖說明

圖1為本發明的流程圖；

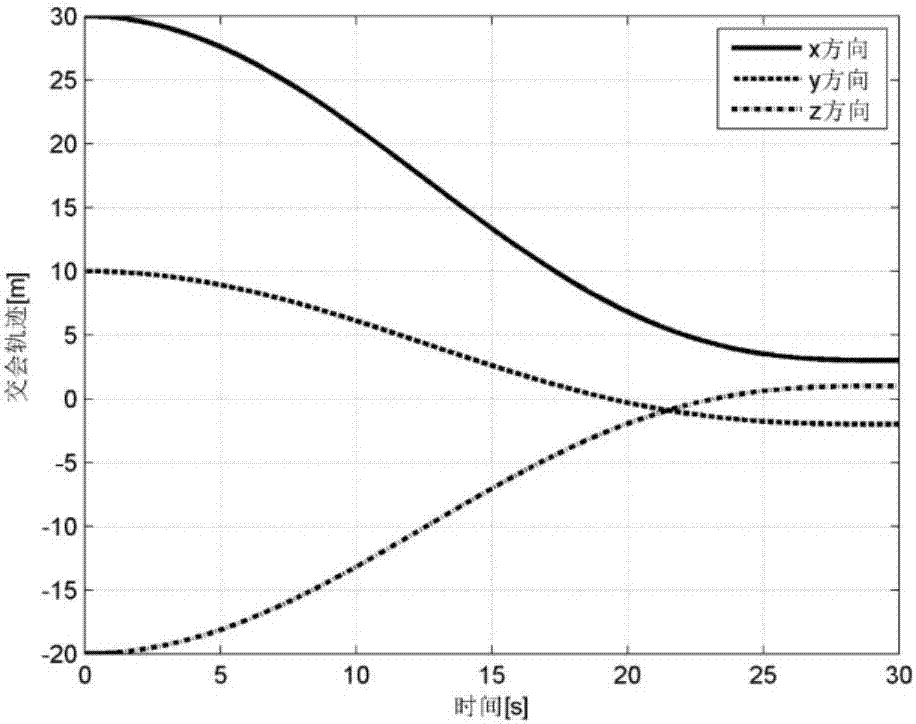
圖2為本發明交會過程中相對位置的變化曲線示意圖；

圖3為本發明交會過程中相對速度的變化曲線示意圖；

圖4為本發明交會過程中控制加速度的變化曲線示意圖。

具體實施方式

tau理論是一種仿生的理論，它是對自然界中的鳥類等動物經過成千上萬年的自然演化和不斷優化所形成的本能運動的歸納和總結，本發明提供了一種基于tau理論的航天器交會制導方法，針對在軌航天器之間的物資和能量傳遞任務，將tau理論這一研究成果應用于航天器在軌交會過程中，利用仿生學的成果設計一條合適交會軌跡，并且保證該軌跡具備一定的最優性和適應性。

請參閱圖1，本發明一種基于tau理論的航天器交會制導方法的具體步驟如下：

s1、建立近距離交會過程中的相對動力學方程，然后引入tau理論，對接近過程中的交會軌跡進行設計；

根據軌道動力學理論可知，在近距離交會過程中由于航天器之間的相對距離十分的小，同時現有的絕大多數的航天器處于近圓軌道上，因此可以采用cw方程來描述兩航天器之間的軌道相對運動，即

其中，[x；y；z]表示跟蹤航天器相對于目標航天器的位置在目標航天器軌道坐標系中的分量表示，n表示目標航天器的軌跡角速率，[fx；fy；fz]表示跟蹤航天器所施加的控制加速度在目標航天器軌道系中的分量表示。

基于tau理論的交會軌跡可以表示為

其中，r(tg)＝[x(tg)；y(tg)；z(tg)]表示交會終端時刻的相對位置，r0＝[x(0)；y(0)；z(0)]表示交會初始時刻的相對位置，tg表示交會過程所持續的時間，kg表示tau_g耦合因子。

上式所表示的交會軌跡可以分解到三個坐標分量，分別為

其中，tg為交會過程所持續的時間，kg為tau_g耦合因子，t為時間變量，[x(t),y(t),z(t)]^t表示t時刻航天器的位置。

s2、由步驟s1中基于tau理論設計的交會軌跡求解接近過程中的交會速度和交會加速度；

對步驟s1中基于tau理論得到的交會軌跡，可以得到對應的交會速度和交會加速度，具體求解如下：

對基于tau理論得到的交會軌跡求導，即可得到交會過程中所需的速度，結果如下：

進而可以得到交會加速度，結果如下：

s3、分析不同的tau-g耦合因子對于交會軌跡的影響，最終確定tau-g耦合因子的合理取值區間；

分析kg對于r(t)的影響如下：

當kg＞1時，r(t)會趨向于0，r(t)一階導數會趨向于無窮，r(t)二階導數會趨向于無窮。

當kg＝1時，r(t)會趨向于0，r(t)一階導數會趨向于2(r(tg)-r0)/tg，r(t)二階導數會趨向于2(r(tg)-r0)/tg²。

當0.5＜kg＜1時，r(t)會趨向于0，r(t)一階導數會趨向于0，r(t)二階導數會趨向于無窮。

當kg＝0.5時，r(t)會趨向于0，r(t)一階導數會趨向于0，r(t)二階導數會趨向于-8(r(tg)-r0)/tg²。

當0＜kg＜0.5時，r(t)會趨向于0，r(t)一階導數會趨向于0，r(t)二階導數會趨向于0。

當kg＜0時，r(t)會趨向無窮0，r(t)一階導數會趨向于無窮，r(t)二階導數會趨向于無窮。

由于交會軌跡的二階導數對應著輸入控制力，而航天器上的控制力輸出是有限的，因此耦合因子kg的選擇范圍為(0,0.5)。

s4、基于步驟s1所設計的交會軌跡，利用逆動力學方法求解該過程中跟蹤航天器所要施加的控制力。

在上述三步中已經得到了交會軌跡的解析表達式，因此根據逆動力學方法，可以求得生成該交會軌跡所需要的控制加速度，基于逆動力學方法的計算如下：

其中，[fzn；fzn；fzn]表示生成交會軌跡所需要的控制加速度。

具體展開如下：

由步驟s3分析可知，為了保證交會軌跡的各階導數閉合，tau-g耦合因子kg的選擇范圍必須為(0,0.5)。

為了說明本方法的可行性及有效性，下面將通過數值進行驗證：

初始時刻服務航天器的相對位置為r(0)＝[30,10,-20]^t(m)，期望的終端位置為r(tg)＝[3,-2,1]^t(m)，交會持續時間tg設置為tg＝30(s)，耦合因子kg＝0.3，仿真結果如圖2-4所示。圖2表示交會過程中相對位置的變化曲線，圖3表示交會過程中相對速度的變化曲線，圖4表示交會過程中控制加速度的變化曲線。

從圖2中可以發現跟蹤航天器能夠順利地到達指定的交會點，確保交會任務的完成；圖3表示按照圖2所示軌跡運動時所需要的速度，從圖3可以看出整個交會過程中所需的速度光滑有界，并且到交會點時速度也同時變為零；圖4表示按照圖2所示軌跡運動時跟蹤航天器所需要的控制加速度，從圖中可以看出控制加速度曲線光滑有界，同時到最終交會點時控制加速度減為零。

從圖2-4可以看出，基于tau理論的航天器交會方法，能夠很好的實現交會要求，同時該方法能夠以解析表達式的形式給出交會軌跡以及該過程中所需的速度和控制加速度，便于星載計算。基于tau理論的航天器交會方法將仿生學成果引入到航天領域，豐富了現有的交會手段，提供了一種新的交會思路。

以上內容僅為說明本發明的技術思想，不能以此限定本發明的保護范圍，凡是按照本發明提出的技術思想，在技術方案基礎上所做的任何改動，均落入本發明權利要求書的保護范圍之內。