弧形微型機電混沌系統的自適應動態面控制方法與流程

本發明涉及弧形微型機電混沌系統，具體涉及弧形微型機電混沌系統的自適應動態面控制方法。

背景技術：

微型機電系統是在微型電子技術(半導體制造技術)基礎上發展起來的，融合了光刻、腐蝕、薄膜、LIGA、硅微型加工、非硅微型加工和精密機械加工等技術制作的高科技電子機械器件。微型機電系統是集微型傳感器、微型執行器、微型機械結構、微型電源微型能源、信號處理和控制電路、高性能電子集成器件、接口、通信等于一體的微型器件或系統。微型機電系統是一項革命性的新技術，廣泛應用于高新技術產業，是一項關系到國家的科技發展、經濟繁榮和國防安全的關鍵技術。微型機電系統側重于超精密機械加工，涉及微型電子、材料、力學、化學、機械學諸多學科領域。它的學科面涵蓋微型尺度下的力、電、光、磁、聲、表面等物理、化學、機械學的各分支。

弧形微型機電混沌系統對外部環境下的初始條件具有敏感性，能呈現非常豐富的動態行為，即工作過程中易產生不規則的混沌振蕩。混沌行為極大地影響弧形微型機電混沌系統的穩定性和安全性，必須要采取措施來改善弧形微型機電混沌系統的性能。

不同激勵幅值R下的弧形微型機電混沌系統相圖和時序圖如圖3和圖4所示，很顯然，系統存在混沌振蕩。弧形微型機電混沌系統龐加萊截面圖如圖5所示。在圖5(a)，(c)，(e)和(f)中存在一些固定的點。當R減小時，吸引不變的軌道開始擴張，如圖5(i)和(h)所示。當R進一步減小時，軌道開始變形，如圖5(g)和(d)所示。當R等于0.02時，系統運動出現不穩定與混沌狀態，如圖5(b)所示。

利用分岔圖來分析弧形微型機電混沌系統周期振動狀態和混沌運動，x₁相對于激勵幅值R的分岔圖如圖6所示。在一定范圍內可以清楚的知道從規則運動到混沌運動的系統動態行為，即混沌振蕩發生在區域B，D，F和I，四周期運動出現在區域H上和二周期運動出現在區域G上。

同時，在實際應用中，由于執行器物理限制、元器件老化以及外界環境影響等因素使得執行器輸入輸出呈現扇形非線性輸入特征。這種特征不可避免地存在于實際控制系統中，并且會造成閉環控制系統的性能下降，甚至導致系統不穩定。基于安全原因和環境保護等方面的考慮，控制系統中的狀態約束和輸出約束不可忽視。研究發現，弧形微型機電混沌系統中的非線性補償問題涉及位置信號及其高階導數的觀測問題，觀測器能夠在系統狀態不完全可測的情況實現系統的閉環控制，解決系統狀態在線估計問題。

微型機電系統具有高度非線性、參數未知、混沌振蕩和多變量等特征。目前微型機電系統研究大部分側重于動力學分析和生產制造，很少從自適應控制方法上去解決其混沌控制問題。另外，通用的控制方法沒有考慮弧形微型機電混沌系統的特征與特點，未能有效解決系統存在扇形非線性輸入、混沌振蕩、未知控制方向、難測量狀態和狀態約束特征等的控制問題。因此，針對弧形微型機電混沌系統的自適應控制問題，迫切地需要提出一些有效的控制方法，從而降低各種因素對系統造成的不利影響，改善其性能，提高可靠性和安全性。

技術實現要素：

發明目的：為了解決現有技術存在的問題，解決弧形微型機電混沌系統在分布式靜電激勵下具有扇形非線性輸入、混沌振蕩、未知控制方向、難測量狀態和狀態約束特征等的自適應控制問題，本發明提供一種弧形微型機電混沌系統的自適應動態面控制方法。

技術方案：一種弧形微型機電混沌系統的自適應動態面控制方法，包括以下步驟：

(1)建立基于Euler-Bernoull梁的弧形微型機電混沌系統動力學模型，確定系統輸出約束條件和扇形非線性輸入條件；根據動力學模型列出弧形微型機電混沌系統非標量方程，定義狀態變量；

(2)設計控制器，通過比較弧形微型機電混沌系統的輸出信號與理想信號進而輸出跟蹤誤差e₁；設計障礙李亞譜諾夫函數，所述障礙李亞譜諾夫函數用于保證輸出信號滿足系統的輸出約束條件，誤差e₁經障礙李亞譜諾夫函數處理后結合Levant微分跟蹤器構成虛擬控制輸入，虛擬控制輸入經一階濾波器濾波后得到濾波器輸出信號α_2f；狀態變量經過擴展狀態觀測器得到變量將濾波器輸出信號α_2f與變量通過比較進而輸出誤差對濾波器輸出信號α_2f求導得到濾波器輸出信號導數

(3)根據步驟(2)得到的誤差e₁和濾波器輸出信號導數構建Nussbaum函數；在backstepping的框架中構建自適應控制律，根據狀態變量x₁和x₂構建帶有自適應控制律的Chebyshev神經網絡；將Nussbaum函數與Chebyshev神經網絡耦合得到實際控制輸入，所述實際控制輸入在滿足扇形非線性輸入條件下輸入弧形微型機電混沌系統；

(4)調節控制器中Levant微分跟蹤器、一階濾波器、擴展狀態觀測器、Chebyshev神經網絡的參數，檢測跟蹤誤差e₁和控制器輸出u的大小；設定一個誤差閾值，當跟蹤誤差e₁小于誤差閾值時，且輸出信號值滿足約束條件時，完成參數的調節。

有益效果：相比較現有技術，本發明提供的一種弧形微型機電混沌系統的自適應動態面控制方法，以在分布式靜電激勵下具有扇形非線性輸入、混沌振蕩、未知控制方向、難測量狀態和狀態約束特征等弧形微型機電混沌系統為對象，基于Euler-Bernoull梁構造動力學模型，設計相應的障礙李亞譜諾夫函數來保證輸出信號嚴格滿足輸出約束條件，結合Levant微分跟蹤器估計理想微分信號的優點，利用Chebyshev神經網絡以任意小的誤差逼近非線性函數的特性和擴展狀態觀測器來在線預估不可測的狀態變量，降低了對物理傳感器的限制，取消了對系統精確數學模型與精準參數的要求，避免了傳統backstepping中對虛擬控制反復求導導致的系數膨脹問題，利用Nussbaum函數處理未知控制方向問題，在backstepping的框架中構造自適應動態面控制器。本發明實現了保證系統瞬態和穩態性能的自適應控制，放松了對系統全狀態已知的假設條件，可以降低弧形微型機電混沌系統不確定性因素對閉環控制性能的影響。

附圖說明

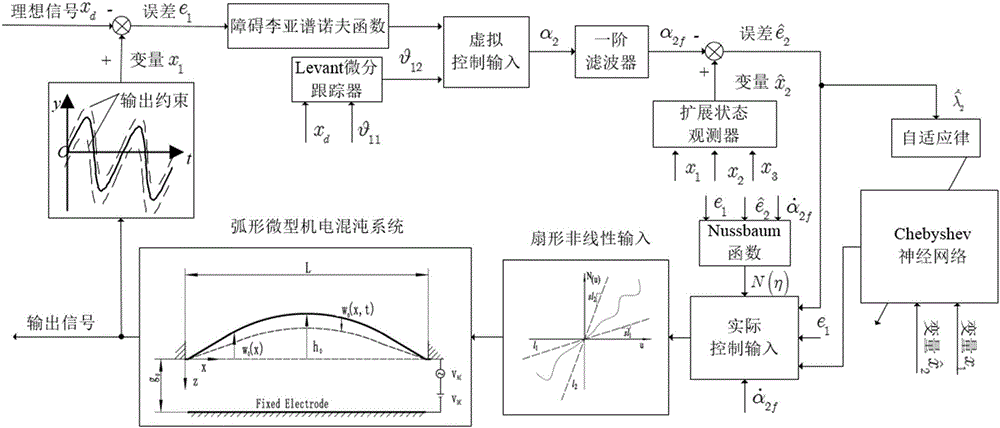
圖1為弧形微型機電混沌系統的自適應動態面控制方法的框圖；

圖2為弧形微型機電混沌系統示意圖；

圖3為不同激勵幅值R下的弧形微型機電混沌系統相圖；

圖4為不同激勵幅值R下的弧形微型機電混沌系統時序圖；

圖5為弧形微型機電混沌系統龐加萊截面圖；

圖6為弧形微型機電混沌系統周期振動狀態和混沌運動的分岔圖；

圖7為系統扇形非線性輸入示意圖；

圖8為系統輸出約束條件示意圖；

圖9為和間的微分跟蹤器性能；

圖10為x₁和間的觀測器性能；

圖11為x₂和間的觀測器性能；

圖12為不同激勵幅值R下的跟蹤性能；

圖13為不同激勵幅值R下的Nussbaum函數；

圖14為不同激勵幅值R下的實際控制輸入。

具體實施方式

下面結合附圖和具體實施方式，對本發明做進一步說明。

如圖1所示，弧形微型機電混沌系統的自適應動態面控制方法，包括以下步驟：

(1)建立基于Euler-Bernoull梁的弧形微型機電混沌系統動力學模型，確定系統輸出約束條件和扇形非線性輸入條件；根據動力學模型列出弧形微型機電混沌系統非標量方程，定義狀態變量；

(2)設計控制器，通過比較弧形微型機電混沌系統的輸出信號與理想信號進而輸出跟蹤誤差e₁；設計障礙李亞譜諾夫函數，所述障礙李亞譜諾夫函數用于保證輸出信號滿足系統的輸出約束條件，誤差e₁經障礙李亞譜諾夫函數處理后結合Levant微分跟蹤器構成虛擬控制輸入，虛擬控制輸入經一階濾波器濾波后得到濾波器輸出信號α_2f；狀態變量經過擴展狀態觀測器得到變量將濾波器輸出信號α_2f與變量通過比較進而輸出誤差對濾波器輸出信號α_2f求導得到濾波器輸出信號導數

(3)根據步驟(2)得到的誤差e₁和濾波器輸出信號導數構建Nussbaum函數；同時根據狀態變量x₁和x₂構建帶有自適應控制律的Chebyshev神經網絡；將Nussbaum函數與Chebyshev神經網絡耦合得到實際控制輸入，所述實際控制輸入在滿足扇形非線性輸入條件下輸入弧形微型機電混沌系統；

(4)調節控制器中Levant微分跟蹤器、一階濾波器、擴展狀態觀測器、Chebyshev神經網絡的參數，檢測跟蹤誤差e1和控制器輸出u的大小；設定一個誤差閾值，當跟蹤誤差e1小于誤差閾值時，且輸出信號值滿足約束條件時，完成參數的調節。

在步驟(1)中，基于Euler-Bernoull梁的弧形微型機電混沌系統動力學方程為：

式中L為細梁長度，A為橫截面積，b為細梁寬度，C_v為粘性阻尼系統，d為細梁厚度，為楊氏模量，I_y為慣性矩，ρ為密度，Ω₀為簡諧荷載頻率，ε_a0為真空電容率，V_DC為直流電壓，V_AC為交流電壓；

弧形微型機電混沌系統的邊界約束條件為：

假設簡諧載荷小于直流靜態載荷，通過坐標變換，利用Galerkin分解法，根據弧形微型機電混沌系統動力學方程列出弧形微型機電混沌系統非標量方程：

式中系統變量定義為：

h＝h₀/g₀；

式中

定義狀態變量x1、x2，

x₁＝q，

考慮扇形非線性輸入特征，并將變量代入弧形微型機電混沌系統非標量方程中得：

其中N(u)表示扇形非線性輸入，其特征關系表示為式(1.6)；y表示系統輸出信號；s_l1＞0和s_l2＞0為斜線l₁和l₂的斜率，斜線l₁和l₂為扇形的兩個邊界，s_M＝max(s_l1,s_l2)。系統輸出y要求滿足一定的約束條件，輸出約束條件是|y|≤k_c1，其中，k_c1表示設定的閾值。

下面詳細介紹自適應動態面控制器：

(一)、Chebyshev神經網絡系統

Chebyshev神經網絡由一系列的正交多項式構成，具有二項遞推公式：

T_i+1(X)＝2XT_i(X)-T_i-1(X),T₀(X)＝1 (1.7)

式中X∈R和T₁(X)通常定義為X，2X，2X-1或2X+1。

Chebyshev神經網絡具有在一個緊湊集上以任意小的精度誤差逼近任意非線性連續函數的能力。同多層神經網絡相比，Chebyshev神經網絡具有較小的計算量。Chebyshev多項式增強模式X＝[x₁,…,x_m]^T∈R^m可以定義為：

ξ(X)＝[1,T₁(x₁),…,T_n(x₁),…,T₁(x_m),…,T_n(x_m)] (1.8)

式中T_i(x_j),i＝1,…,n,j＝1,…,m表示Chebyshev多項式，n表示Chebyshev多項式的除數，ξ(X)表示Chebyshev多項式基函數。

由于Chebyshev神經網絡具有萬能逼近能力，未知非線性函數f_CNN(X)可以估計：

f_CNN(X)＝θ^*Tξ(X)+δ (1.9)

式中δ表示有界的神經網絡逼近誤差，θ*表示最優權值矢量，并滿足

式中Ω_θ和D_X表示緊湊集的界限θ和X。另外，對任意正定常數δ₀，|δ|≤δ₀滿足。

(二)、控制器設計

a)設計擴展狀態觀測器

利用擴展狀態觀測器觀測變量

式中z₀表示參考信號f_r(τ)的估計值，z_i,i＝1,…,n表示其導數和k_i,i＝1,…,n表示設計常數。

從前面可知，如果n等于3，設計如下擴展狀態觀測器

觀測器誤差滿足

式中和表示x_i,i＝1，2，3的估計值。k_o、k₁、k₂為設計常數。

b)定義有界誤差變量

式中表示x₂的估計值，間接虛擬控制α_2f將在接下來的內容中給出。

連續函數N(η)：R→R被稱為是一個Nussbaum增益函數，具有如下特性：

Nussbaum增益函數定義為：若V(.)和η(.)在區間[0∞)是光滑函數，同時V(t)≥0，那么N(.)為光滑的Nussbaum增益函數。此時有：

式中常數c₁＞0，g(t)是非零常數，c₀表示某個合理的常數，同時V(t)，η(t)和在區間[0∞)上必定有界。

變量x₂受到物理傳感器和交叉耦合極小化的影響，通常不可測。為了解決這個問題，利用擴展狀態觀測器來精確估計它的值，即觀測誤差為

選擇障礙李亞譜諾夫函數

其中d_b表示理想信號的上限值，和約束關系不違反。

對V₁求導

式中y₂表示一階濾波誤差且等于α_2f-α₂。

基于Levant微分跟蹤器，可以替代則

其中r₁₁與r₁₂表示常量，表示設定的閾值；為Levant微分跟蹤器的變量，為Levant微分跟蹤器的輸出值。

結合障礙李亞譜諾夫函數及Levant微分跟蹤器，構成虛擬控制輸入：

式中c₁表示常量；

把(1.21)代入(1.19)，則

c)在backstepping的框架中構建自適應控制律，根據狀態變量x₁和x₂構建帶有自適應控制律的Chebyshev神經網絡，其自適應控制律的具體設計方法為：

設一階濾波器濾波時間常數為τ₂，虛擬控制輸入為α₂，可得

存在

對y₂求導得

式中為連續函數，

根據Young’s不等式，得到不等式：

進而得到誤差的公式為：

其中為觀測誤差的導數，觀測誤差所以

f₂(·)為復雜的非線性項，α₂的導數會導致系統膨脹和計算負擔。由于制造誤差，環境擾動和建模誤差的影響，系統參數諸如μ,h,α₁,β,ω₀,R,b₁₁是不確定的。系統參數擾動會引發弧形微型機電混沌系統的混沌振蕩。因此，控制設計過程中要考慮這些非線性特征和因素。鑒于Chebyshev神經網絡具有萬能逼近特性，利用它來估計f₂(·)。即，存在

式中δ₂為神經網絡逼近誤差。

引入變量

式中表示λ₂的估計值；

選擇李亞譜諾夫函數

式中γ₂表示設計常數。

對V₂求導得

由(1.21)可知

結合公式(1.22)、(1.28)、(1.32)、(1.31)得不等式：

式中a₂表示設計常數；

實際控制律設計為：

自適應控制律設計為

式中c₂和m₂表示設計常數；且有

存在關系把(1.34)-(1.36)代入(1.33)，得到

式中

選擇參數τ₂滿足關系利用楊氏不等式，(1.37)重寫為

針對弧形微型機電混沌系統在分布式靜電激勵下具有扇形非線性輸入，混沌振蕩，難測量狀態和狀態約束特征，融合擴展狀態觀測器(1.21)和微分跟蹤器(1.20)到控制器中，設計帶有自適應控制律(1.35)-(1.36)和濾波器(1.23)的自適應動態面控制器如(1.34)所示，那么系統所有信號諸如e₁，保持全局一致有界，且輸出約束不被違反，跟蹤誤差快速收斂到零附近。

利用Lyapunov理論證明閉環系統所有閉環信號全局一致有界：

對V求導：

式中C₀＝min{2×c₁,2×(c₂-0.5),m₂}＞0和

對(1.39)兩邊同時乘以得到

給定對通過對(1.40)積分，得到

因此，e₁,和屬于緊湊集

由上面可知，弧形微型機電混沌系統所有信號有界。特別是，有不等式

由于y(τ)＝e₁+x_d，和|x_d|≤d_b，很容易得到因此，所提控制方案保證了y滿足約束條件。

根據(1.5)描述的弧形微型機電混沌系統，Chebyshev多項式階數為3，根據弧形微型機電混沌系統非標量方程，將Chebyshev多項式基函數設計如下：

雖然RBF神經網絡作為一種逼近器可以解決動態面系數膨脹問題和具有以任意精度逼近非線性函數的能力，但應用RBF神經網絡時需要事先知道高斯基函數的中心與權值，而Chebyshev神經網絡僅僅只需要輸入變量信息。

調節參數c₁，c₂，k₀，k₁，k₂，r₁₁，r₁₂，γ₂，a₂和m₂保證跟蹤誤差趨于無窮小，并確保了閉環系統滿足一定的輸出約束條件，使自適應動態面控制技術具有對系統參數擾動的魯棒性以及混沌行為的抑制能力。

弧形微型機電混沌系統如圖2所示，參數取值為α₁＝7.993，β＝119.9883，h＝0.3，R＝0.02，μ＝0.1和ω₀＝0.4706。為了求解常微分方程，采用四階龍格庫塔算法求解，同時積分時間設置為2000以上。

給定時變參考信號x_d＝0.35sin(3τ)。控制輸出滿足約束條件|y|＜k_c1＝0.39，可以得到扇形非線性輸入可以表達為N(u)＝(0.75+0.25sin(u))u，如圖7所示。根據弧形微型機電混沌系統的自適應動態面控制方法，各參數選擇如下：將一階濾波器的時間常數τ₂設置為0.01，擴展狀態觀測器的參數選擇為k₀＝k₁＝20，k₂＝19。控制器增益與參數選擇為c₁＝c₂＝10，γ₂＝1，m₂＝15，a₂＝5。二階微分跟蹤器參數選擇為r₁₁＝r₁₂＝6，初始值設定為0.01。

設計二階微分跟蹤器在線估計圖9展示了和間的性能，兩條線基本重合且相對誤差小于0.05。圖10-11展示了高階擴展狀態觀測器的優越性能。從圖可知，擴展狀態觀測器能夠精確估計狀態變量，同時放寬對物理傳感器的限制。盡管弧形微型機電混沌系統具有扇形非線性輸入，狀態約束和混沌振蕩等特征，觀測器還是以很小的誤差精確估計狀態變量。

為了對比方便，不同參數下的性能曲線放在一張圖中。圖12展示了e1在不同參數下的跟蹤性能(也可以看出x₁的跟蹤性能)。很明顯，4種工況(即R＝0.01,0.02,0.15,0.25)的實際軌跡與參考軌跡基本吻合，且實際與理論性能曲線間的差值為±0.01。

另外，應用障礙李亞譜夫函數后|y|＜k_c1約束條件得以保證。同圖3的相圖和圖4的時序圖對比，應用所提方案后弧形微型機電混沌系統在極短時間內實現狀態穩定，同時與之相關的混沌振蕩得到徹底抑制。

由于扇形非線性輸入和控制輸入方向未知，如不采取有效措施必定會導致控制器失效。圖13表示不同R值的弧形微型機電混沌系統Nussbaum函數曲線。盡管系統參數遭受到外界干擾，4條Nussbaum function曲線基本保持一致。

扇形非線性輸入存在于弧形微型機電混沌系統的控制輸入中。它的存在影響控制性能甚至導致控制器出現顫抖現象。圖14揭示了不同R值下的控制輸入。由圖可知，顫抖現象極大地被弱化，同時所設的控制器具有一定的魯棒性。