一種氣動伺服加載系統的非線性復合控制方法與流程
本發明涉及機電伺服控制領域,具體地指一種氣動伺服加載系統的非線性復合控制方法。
背景技術:
氣動系統以其能源清潔、無污染,成本低,簡單易實現,功重比高等優勢適用于工業應用,但是另一方面,由于氣體本身的低剛度、弱阻尼,氣動系統參數不確定性及未建模動態等不確定性等特征制約了氣動伺服控制技術的進一步研究及應用。
技術實現要素:
本發明就是針對現有技術的不足,提供了一種動態性能良好的氣動伺服加載系統的非線性復合控制方法。
為了實現上述目的,本發明所設計的氣動伺服加載系統的非線性復合控制方法,其特征在于:包括以下步驟,
1)設計氣動伺服加載控制系統;
2)建立系統動力學和熱力學平衡方程,并得出系統誤差表達式;
3)設計一個狀態變換和一個輸入變換,將系統誤差由非線性控制轉為線性線性定常控制;
4)利用李雅普諾夫方法降低系統誤差控制存在的動態不確定性;
5)采用ITAE優化控制算法,保證系統誤差控制的快速性和跟蹤進度。
進一步地,所述的氣動伺服加載控制系統包括原理和結構相同的加載通道和被加載通道,所述加載通道和被加載通道的輸出端固定連接,輸入端連接在同一氣源調節裝置上,所述加載通道和被加載通道均包括氣動馬達和氣動閥,所述氣動閥進氣端與氣源調節裝置連接,所述氣動閥出氣端與氣動馬達連接。更進一步地,所述步驟2)的具體過程如下:
21)在理想的假設條件下,利用流量連續方程和系統熱力學方程,根據質量守恒定律,得出氣動馬達兩腔的狀態方程
式中,R表示空氣的氣體常數,T11為馬達I腔的溫度,Ps表示氣源壓強,p0表示大氣壓強,P11為馬達I腔的壓強,P21為馬達Ⅱ腔的壓強,表示質量流量變化率,V11=Dm(θ10+θ0),V12=Dm(θ20+φ-θ0),S1in,S1out為比例閥進氣口的有效開口面積;S2in,S2out為比例閥進排氣口的有效開口面積,其中S1in=S2out,S1out=S2in;
22)將兩腔狀態方程轉為仿射型形式:
式中,Pi表示氣動擺動馬達兩腔的壓強,ui表示比例流量閥的控制信號,θ表示馬達的旋轉角度,表示馬達葉片的角速度,t表示時間;
23)由兩腔狀態方程的仿射型形式得出兩腔壓強差產生的力矩表達式:
式中,Dm表示馬達的排量,u表示控制量輸入,即伺服閥輸入信號;
24)將兩腔壓強差產生的力矩表達式轉化為仿射型形式:
再進一步地,所述系統誤差表達式為:
式中,Mp表示兩腔壓差產生的力矩,Mf表示系統的摩擦力矩;Md為期望跟蹤的信號。
再進一步地,步驟3)的具體過程如下:
31)設狀態變換為:
則
其中,為期望跟蹤信號的導數;
32)設輸入變換為:
式中,v是虛擬控制量;
33)將狀態控制線性化:
再進一步地,所述步驟4)的具體過程為,
41)將輸入量v設計為:v=vl+vnd
其中,令vl=-KX,
式中,vl為線性狀態反饋設計方法設計反饋控制變量,線性控制分量采用極點配置方法進行設計,同時通過Matlab的LMI工具箱進行求解,vnd為非線性控制變量;
42)設計標稱李雅普諾夫方程為:
則:
令
式中,表示摩擦力模型及相關的不確定性
43)將42)中vnd帶入整理得:
對于-k1|BTP-1X|2|δ|2+|η1||BTP-1X||δ|,當時有最大值因此在半徑為的球外總是負的,對任意初始狀態,即使在不確定性動態的上界未知的情況下,閉環系統的解(X)是一致有界的,根據出處為“Slotine J J,Li W.Applied nonlinear control[M].China Machine Press,2004.”的引理,對任意初始狀態,即使動態不確定性的上界未知的情況下,閉環系統的解(X)仍然一致有界,采用ITAE優化控制算法進行優化,同時滿足跟蹤快速性和跟蹤精度的要求,證明如下:
對于
令R=PQP-1,
則有:
對于有而XTPX≥λmin(P)||X||2,則有閉環系統的解一致有界,即該系統穩定且能保證一定的跟蹤精度。
本發明的優點在于:
該方法采用反饋線性化,通過極點配置,消除氣動伺服加載系統的不穩定極點,使系統收斂;針對系統對自身以及外界的動態不確定性,存在不能確保魯棒性的缺陷,采用李雅普諾夫再設計方法使系統即使存在較大的動態不確定性時,具有魯棒性。該方法采用ITAE優化控制算法,能同時保證系統的快速性和跟蹤精度的要求。
附圖說明
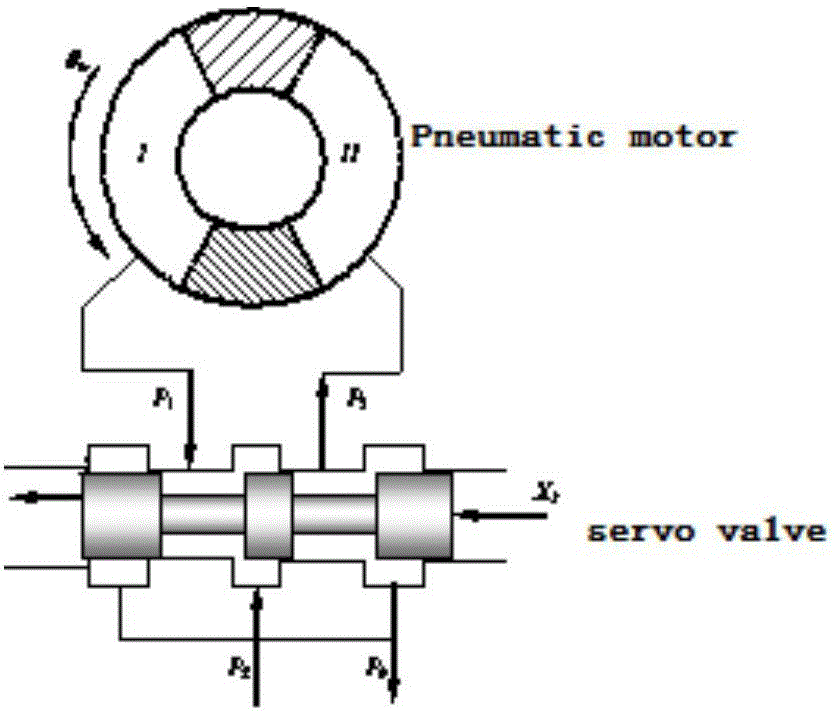
圖1為氣動伺服加載系統。
圖2為氣動伺服加載系統中的閥控缸。
圖3為本發明氣動伺服加載系統的非線性復合控制方法原理圖。
圖4為60°20Nm0.5hz正弦PID加前饋控制與非線性復合控制方法仿真結果比較。
圖5為本發明的60°10Nm 1Hz與PID加前饋控制與非線性復合控制方法仿真結果比較。
圖6為本發明的60°20Nm0.5hz PID加前饋控制與非線性復合控制方法實驗結果比較。
圖7為本發明的60°10Nm 1Hz正弦對頂加載PID加前饋控制與非線性控制方法實驗結果比較。
具體實施方式
下面結合附圖和具體實施例對本發明作進一步的詳細描述:
一種氣動伺服加載系統的非線性復合控制方法,包括以下步驟,
1)設計氣動伺服加載控制系統;
2)建立系統動力學和熱力學平衡方程,并得出系統誤差表達式;
3)設計一個狀態變換和一個輸入變換,將系統誤差由非線性控制轉為線性線性定常控制;
4)利用李雅普諾夫方法降低系統誤差控制存在的動態不確定性;
5)采用ITAE優化控制算法,保證系統誤差控制的快速性和跟蹤進度。
其中,氣動伺服加載控制系統包括原理和結構相同的加載通道和被加載通道,加載通道和被加載通道的輸出端固定連接,輸入端連接在同一氣源調節裝置上,加載通道和被加載通道均包括氣動馬達和氣動閥,所述氣動閥進氣端與氣源調節裝置連接,所述氣動閥出氣端與氣動馬達連接。圖1所示的氣動伺服加載系統,左邊是加載通道,進行力矩伺服控制,右邊是被加載通道,進行位置伺服控制,兩通道采用固定聯接。整個系統的設計目的是在被加載通道進行既定的位置運動時,實際工況中來源于實時采樣,加載通道能夠盡可能的跟蹤復現任意負載。為適當簡化數學模型,作如下假設:
a)所用工作介質為理想氣體,滿足理想氣體狀態方程;
b)供氣壓力P和溫度恒定;
c)氣缸中的氣體是均勻的,每一瞬時腔中每一個點的狀態參數相同;
d)氣缸與外界以及兩腔之間沒有泄漏;
e)氣體在流過閥口或其它節流孔時的流動狀態均視為等嫡絕熱過程。
由以上氣動伺服加載系統,建立系統動力學和熱力學平衡方程,并得出系統誤差表達式。
在氣動系統中,當氣體流經任何元器件或者管道時,均視為流經一定面積的小孔,并用小孔的流量特性表示氣體經過閥口的流動規律。不同于液體和電流特性的是,氣體流經小孔時隨著上下游的壓強比的變化會出現流量的飽和特性,流經小孔的質量流量方程如下:
式中Qma為流經小孔的氣體質量流量;Se為小孔的等效面積;Pu為小孔上游的壓強;Pd為小孔下游的壓強;KG為氣體常數;T10為小孔上游氣體的溫度。
在圖2中,圍繞馬達I腔取一單元,流入該單元的質量變化率為:
由氣體狀態方程有:
展開得到:
由于加載過程中活塞運動速度較快,馬達腔內氣體來不及與周圍環境進行熱交換,將加載過程近似為絕熱過程,該過程中氣體溫度與壓強關系為:
將(5)式代入(4)式得到如下方程:
其中qma為流經馬達I腔的質量流量;R為氣體常數;P10為馬達I腔的初始壓強;P11為馬達I腔的壓強,V10馬達I腔的初始體積;V11為馬達I腔的體積;T10為馬達I腔的初始溫度;T11為馬達I腔的溫度。根據質量守恒定律,令式(1)等于(6),經過推導得到馬達I、II兩腔的狀態方程如下:
其中:V11=Dm(θ10+θ0),V12=Dm(θ20+φ-θ0),S1in,S1out為比例閥進氣口的有效開口面積;S2in,S2out為比例閥進排氣口的有效開口面積,其中S1in=S2out,S1out=S2in。
加載系統擺動馬達轉子力矩平衡方程為:
當有負載時:
式中,ΔP為擺動馬達兩腔的壓差,Jm為加載系統的轉動慣量,θm為加載系統的角位移,Bm為加載系統的粘性阻尼系數,Gε為力矩傳感器扭轉剛度,θl為負載等效角位移,Jl為負載等效轉動慣量,Bl負載等效粘性阻尼系數,Gl為負載等效扭轉剛度,θf為舵機輸出軸等效角位移。
氣動伺服加載系統的反饋線性化如下:
將(7)、(8)表示成如下仿射型形式:
其中:
其中:k=1.4表示空氣的比熱,Pi表示氣動擺動馬達兩腔的壓強;ui表示比例流量閥的控制電壓信號;Pu表示小孔上游的壓強;Pd表示小孔下游的壓強;Pcr表示臨界壓力比;p0表示大氣壓強;Ps表示氣源壓強;R表示空氣的氣體常數;θ表示馬達的旋轉角度;表示馬達葉片的角速度;T表示馬達兩腔在工作過程中的溫度。由兩腔壓強差產生的力矩表達式如式(13)所示:
令:
其中,Mp表示兩腔壓差產生的力矩,Δp表示馬達兩腔的壓差;Dm表示馬達的排量。由式(13-15)得到氣動伺服加載系統的仿射型表達式如下:
令比例流量閥的控制電壓信號u與閥芯開口面積(Se)的關系為Se=Ku·|u|。進一步將系統方程表示為:
Mout=Mp+Mf+MJ
其中,Mout表示系統輸出的力矩;Mf表示系統的摩擦力矩;MJ表示系統的慣性力矩,由于該系統的馬達轉動慣量比較小,在此將其忽略。
對于力矩伺服加載系統,其系統的輸出表達式為:
對于氣動擺動馬達,其自身的轉動慣量遠小于負載的轉動慣量,可將其忽略。氣動伺服加載系統的誤差表達式為:
其中:Md為期望跟蹤的信號。
鑒于氣動系統在穩態時容易產生爬行現象,在控制器設計過程中,引入積分控制分量,以減小系統的穩態誤差,狀態變換設計為:
則:
其中,為參考指令的導數;
輸入變換設計為:
其中αn,βn分別表示α,β的名義值,將式(17)帶入式(21)得到:
將(23)帶入(21)得到:
通過上述變換,將原系統中利用控制量u來控制非線性系統的問題轉化為用新的控制量v來控制系統(24)的問題了。對于轉換后的線性系統,采用極點配置方法解決系統的非線性問題,但當系統存在一定的動態不確定性時,如參數不確定性及未建模動態等,單純采用反饋線性化理論設計控制器不能確保系統的魯棒性,基于此,本文采用李雅普諾夫再設計方法,在標稱系統的Lyapunov函數中設計一個附加的控制分量,使被控對象即使存在有較大的動態不確定性時,而總的控制仍然能夠達到穩定,具有魯棒性。控制器設計如下,令:
v=vl+vnd (25)
對于式(25),采用線性狀態反饋設計方法設計反饋控制變量vl=-KX,得到如下表達式:
對于式(25),線性控制分量采用極點配置方法進行設計,同時通過Matlab的LMI工具箱進行求解。
下面采用李雅普諾夫再設計方法設計非線性控制分量以及穩定性分析:
對于一個給定的正定矩陣Q存在唯一的正定矩陣P,使得:
設標稱系統(24)李雅普諾夫方程為:
對該方程進行求導可得:
設非線性控制分量的表達式為:
其中表示系統動態不確定性,η1=max(|η|)表示該動態不確定性的上界(未知),將(31)帶入式(30)則有:
對于-k1|η||BTP-1X|2|δ|2+|η||BTP-1X||δ|,當時有最大值因此在半徑為的球外總是負的,對任意初始狀態,即使動態不確定性的上界未知的情況下,閉環系統的解(X)仍然一致有界,采用ITAE優化控制算法進行實時求解同時滿足跟蹤快速性和跟蹤精度的要求,證明如下:
對于
令R=PQP-1,
則有:
對于有而XTPX≥λmin(P)||X||2,則有閉環系統的解一致有界,即該系統穩定且能保證一定的跟蹤精度。
用以上仿真模型進行“PID+前饋”與“非線性復合”控制方法的仿真比較,其結果如附圖所示,附圖4所示為在位置系統做0.5Hz,60°正弦的干擾情況下,在前饋+PID控制下,誤差范圍在±4Nm以內,在非線性控制方法下,誤差被控制在±2.5Nm以內,明顯提高系統精度。
附圖5所示為在位置系統做1Hz,60°正弦的干擾情況下的對頂加載仿真結果比較,在“PID+前饋”控制下,誤差最大幅值在5Nm以內,在非線性控制方法下,誤差最大幅值在2.5Nm以內,誤差最大幅值縮小一半;“爬行+抖振”現象得到改善;同時穩態誤差很快收斂到零點附近。仿真結果表明:非線性阻尼控制方法有效提高系統控制品質。
附圖6所示與附圖5是在相同條件下的兩種控制方法的實驗結果對比,從結果曲線可以看出,實驗結果能夠分別與相應的仿真吻合。對應實驗曲線的誤差最大幅值分別為1Nm和2.5Nm,相對于“PID+前饋”控制方法,非線性復合控制提高了動態跟蹤精度及穩態誤差,改善了“爬行+抖振”現象。控制方法在實際中能夠有效提高控制品質。在實驗條件下,誤差信號的抖振相對較多,這一方面是在實驗過程中控制參數偏大,另一方面是因為在采樣過程中存在一定的噪聲導致的。
附圖7是在相同條件下的兩種控制方法的實驗結果對比,從結果曲線可以看出,實驗結果分別與相應的仿真對應,非線性復合控制方法在提高控制精度,穩態誤差,改善“爬行+抖振”現象方面均優于“PID+前饋”控制方法。但是在實驗條件下,誤差信號有抖振現象,這主要是因為在實驗過程中存在一定的采樣噪聲導致的。
根據幾組數據得出來的實驗結果表明:氣動伺服加載系統的復合非線性復合的控制方法可以較大提高系統的加載跟蹤精度,同時在消除抖振現象方面比PID結合前饋控制方法有很好的改進。值得進一步推廣應用。
- 還沒有人留言評論。精彩留言會獲得點贊!